АВТОМАТОВ АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ

Расстановка ударений: АВТОМА`ТОВ АЛГЕБРАИ`ЧЕСКАЯ ТЕО`РИЯ

АВТОМАТОВ АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ - направление в автоматов теории, характеризующееся использованием алгебраич. средств в изучении автоматов. А. а. т. основана на том, что автоматы можно рассматривать как нек-рые специальные алгебры или алгебраические системы. Кроме того, события, представимые конечными автоматами, относительно операций объединения, произведения и итерации образуют алгебру, порождаемую конечным множеством так наз. элементарных событий, каждое из к-рых состоит из одного однобуквенного или пустого слова. Алгебраический подход позволяет непосредственно использовать алгебраич. результаты в теории автоматов, а также помогает в нек-рых случаях установлению связи теории автоматов с другими областями математики. Так, с помощью теории автоматов были получены доказательства разрешимости нек-рых арифметических теорий второй ступени, а также новое, более простое, решение ограниченной Бернсайда проблемы.

С алгебраич. точки зрения, автомат (конечный или бесконечный) 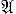= (A, S, В, φ, ψ) является трехосновной алгеброй, т. е. алгеброй с тремя множествами A, S, В элементов и двумя операциями φ : S × А → S и ψ : S × A → B. С другой стороны, переходную систему (A, S, φ), где А = {a₁, ..., a_n} - входной алфавит, S - множество состояний (см. Автомат конечный), можно рассматривать как алгебру 〈 S, a₁, ..., a_n 〉 с унарными операциями, обозначаемыми буквами а, - входного алфавита А и такими, что a_i s_j = φ (s_j, a_i). Таким образом, для автоматов естественно определяются такие понятия, как автоматов гомоморфизм, изоморфизм, подавтомат и т. д. Вместе с тем этот подход позволяет сопоставить автомату 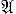= (A, S, В, φ, ψ) полугруппу преобразований множества S с операцией суперпозиции, порожденную операциями a_i, так что для произвольных a_i, a_j из А и s из S положено

a_i a_j S = φ (φ (s, a_i), a_j).

Эта полугруппа наз. полугруппой автомата 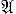, она используется как средство описания определенных свойств автоматов (классификация, разложимость, изоморфизм и т. д.) на алгебраич. языке. В то же время всякой полугруппе Q с единицей можно сопоставить автомат с заданным входным алфавитом А = {a₁, ..., a_n} и множеством состояний Q следующим образом. Каждой букве a_i из А ставят в соответствие нек-рый элемент q_i из Q и тогда функцию переходов ф можно определить так: φ (s, a_i) = qq_i . Полугруппа такого автомата изоморфна подполугруппе полугруппы Q, порожденной элементами q₁, ..., q_n, и тем самым в случае, если q₁, ..., q_n суть образующие полугруппы Q, полугруппа автомата изоморфна исходной полугруппе Q. Полугруппа автомата очевидным образом изоморфна факторполугруппе входной полугруппы всех слов в алфавите А (множество A^*) с операцией последовательного соединения слов (конкатенация) по конгруэнции

R = {(α, β): α, α ∈ A^* и ∀ s ∈ S (φ (s, α) = φ (s, β))}.

Для произвольного состояния s ∈ S конгруэнция R является максимальной подконгруэнцией отношения

R_s = {(α, β): α, α ∈ A^* и (φ (s, α) = φ (s, β))}.

Это означает, в частности, что событие, представимое инициальным акцептором 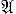_s = (A, S, φ, S'), является объединением нек-рых R-классов. Поскольку полугруппа автомата характеризует его с точностью до изоморфизма, то различным классам полугрупп соответствуют свои классы автоматов. В том случае, когда полугруппа автомата является свободной, или абелевой, или циклической, или нильпотентной и т. п., или, наконец, группой, автомат называется, соответственно, свободным, абелевым, циклическим, нильпотентным, групповым (или перестановочным). Другой подход, связанный с алгебраич. классификацией функций переходов и выходов, приводит к классам линейных, подстановочных и др. автоматов (см. Автомат). Подстановочные автоматы реализуют взаимно однозначные функции и используются в теории кодирования. Линейные автоматы представляют интерес в связи с простотой их схемной реализации.

Автомат (A, S, В, φ, ψ) наз. линейным автоматом (л. а.), если A, S и В - линейные пространства над нек-рым полем Р,

φ (s, а) = φ₁ (s) + φ₂ (а), ψ (s, а) = ψ₁ (s) + ψ₂ (а),

где φ₁, φ₂, ψ₁, ψ₂ - линейные отображения соответственно: S в S, А в S, S в В, А в В. Обычно предполагается, что поле Р конечно, а пространства A, S, В конечномерны; в этом случае л. а. является конечным автоматом. Если в представлении конечного акцептора в виде алгебры, операциями к-рой являются буквы входного алфавита, допустить многоместные операции, то полученное обобщение наз. автоматом над термами (автоматом над деревьями, обобщенным автоматом). Такие автоматы используются для доказательства разрешимости нек-рых математич. теорий второй ступени.

Лит. : [1] Алгебраическая теория автоматов, языков и полугрупп, М., 1975; [2] Глушков В. М., «Успехи матем. наук», 1961, т. 16, №5, с. 3-62; [3] Тэтчер Д ж. В., Райт Д ж. Б., в кн. : Кибернетический сборник, в. 6, М., 1969, с. 112-44. См. также лит. к статье Автомат.

В. Б. Кудрявцев, Ю. И. Янов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.