АВТОМАТ КОНЕЧНЫЙ

Расстановка ударений: АВТОМА`Т КОНЕ`ЧНЫЙ

АВТОМАТ КОНЕЧНЫЙ - математическая модель устройства с конечной памятью, преобразующего дискретную информацию. А. к. является одним из важнейших видов управляющих систем. Содержательно А. к. можно охарактеризовать как устройство, имеющее входной и выходной каналы и находящееся в каждый из моментов дискретного времени, наз. тактовыми моментами, в одном из n состояний s₁, s₂, ..., s_n . По входному каналу в каждый тактовый момент в устройство поступают сигналы - буквы входного алфавита. В те же моменты по выходному каналу устройство выдает сигналы - буквы выходного алфавита. С соответствующей точки зрения, к таким устройствам могут быть отнесены формальные системы, реальные автоматы, живые организмы и т. п.

Существуют различные подходы к определению понятия А. к. При макроподходе, т. е. когда интересуются только внешним поведением устройств, определение А. к. может быть дано в виде совокупности функций, либо в виде конечного ориентированного графа, либо в алгебраич. форме - в виде конечной алгебры с унарными операциями (см. Автоматов способы задания). При микроподходе А. к. задается множеством элементов и схемой их соединения, т. е. в этом случае кроме функционирования описывается и строение автомата, в связи с чем это понятие обычно наз. структурным, а сами А. к. - структурными автоматами, или автоматными сетями.

Макроподход. А. к. - это система (A, S, В, φ, ψ), где А, S, В - конечные, как правило непустые, алфавиты, наз., соответственно, входным алфавитом, множеством состояний и выходным алфавитом; φ - функция переходов, отображающая множество S × A в S; ψ - функция выходов, отображающая S × A в В. Такие А. к. иногда называются автоматами Мили. В случае, когда функция выходов ψ отображает S в В (т. е. не зависит от букв входного алфавита), А. к. называют автоматом Мура. Всякий автомат Мура является автоматом Мили.

Важнейшей характеристикой А. к. является его поведение (см. Автомата поведение), к-рое может быть определено по-разному. В зависимости от того, какой тип поведения рассматривается, А. к. подразделяются на преобразователи, акцепторы (распознаватели), генераторы и др. Чтобы определить основные виды поведения А. к., функции φ и ψ распространяют на множество S × А^* (где А^* - множество всех слов в алфавите А, включая пустое слово ∧):

φ (s, ∧) = s, φ (s, α а) = φ (φ (s, α), а), ψ (s, ∧) = ∧, ψ ((s, α а) = ψ (φ (s, α), а)

(здесь s ∈ S, α ∈ А^*, а ∈ А, а запись α а обозначает слово, получаемое путем приписывания буквы а к слову α). Таким образом распространенные функции φ (s, α), ψ (s, α) для произвольных s и α описывают соответственно состояние, в к-рое переходит автомат из состояния s под действием входного слова α, и выходную букву, к-рая выдается автоматом в момент поступления последней буквы входного слова α. Пусть 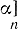обозначает начало длины n слова α и 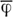(s, α), 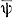(s, α) - слова в алфавитах S и В, определяемые следующим образом:

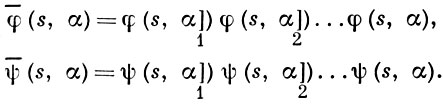
Функции 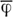(s, α), 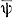(s, α) описывают уже последовательность всех состояний, в к-рых находился автомат при поступлении в него букв слова α, а также выходное слово, т. е. последовательность букв выходного алфавита, выдаваемых автоматом под воздействием входного слова α. Тернарное отношение

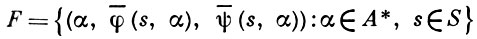
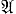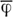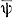наз. функционированием А. к. = (A, S, В, φ, ψ). Функции и естественно распространяются и на бесконечные последовательности (сверхслова) в алфавите А. Поэтому под функционированием А. к. иногда понимают отношение вида F, в к-ром α - произвольное сверхслово. В этом случае значение функции φ (s, α) определяется как множество всех тех и только тех состояний, к-рые встречаются в последовательности 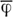(s, α) бесконечное число раз.

А. к. с выделенным начальным состоянием s₁ наз. инициальным и обозначается 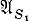. Поведением инициального А. к. 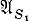наз. обычно одно из следующих трех отношений.

1) Функция f(а) = 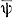(s₁, α), отображающая А^* в В^* (или А^∞ в В^∞, где А^∞, B^∞ - множества всех сверхслов в алфавитах А и В соответственно). Эта функция наз. функцией вычислимой, или реализуемой, инициальным А. к. .

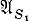2) Множество L_S' ⊆ А^*, определяемое для выделенного множества S' ⊆ S заключительных состояний так:

L_S' = {α ∈ A^* : φ (s₁, α) ∈ S'}.

Множество L_S' наз. событием, представимым А. к. 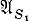с множеством S' заключительных состояний.

3) Множество значений функции f(α) = 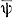(s₁, α) для всевозможных α из А^*, называемое множеством, перечислимым данным А. к. .

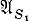4) Множество М_γ ⊆ A, определяемое для системы γ подмножеств множества S следующим образом:

М_γ = {α ∈ A^∞ : φ (s₁, α) ∈ γ }.

Множество М_γ наз. сверхсобытием, представимым А. к. 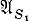с системой γ заключительных подмножеств состояний. А. к. с поведением типа 1) наз. конечным преобразователем, а с поведением типа 2) - конечным распознавателем, или акцептором.

Если в качестве входного и выходного алфавитов взять декартовы произведения А₁ ×... × А_m и B₁ ×... × B_n, соответственно, то поведением типа 1) будет набор из n функций от m аргументов. В этом случае говорят, что автомат имеет m входов и n выходов, причем алфавиты А₁, ..., А_m, В₁, В_n наз., соответственно, входными и выходными алфавитами такого автомата. Класс событий, представимых А. к., и класс функций, вычислимых А. к., могут быть описаны различными математич. средствами. Основной результат состоит в том, что события, представимые А. к., совпадают с так наз. регулярными событиями, а функции, вычислимые А. к., совпадают с ограниченно-детерминированными функциями. Кроме того, класс множеств, перечислимых А. к., совпадает с классом событий, представимых А. к.

Относительно поведений 2), 3) и 4) автоматы Мура эквивалентны автоматам Мили в том смысле, что для всякого автомата Мили найдется эквивалентный ему, т. е. имеющий то же самое поведение, автомат Мура, и обратно. Для поведения 1) это неверно. Однако, если в автоматах Мура вместо 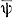брать функции вида

то автоматы Мура будут эквивалентны автоматам Мили.

Автомат Мура 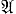= (A, S, В, φ, ψ) наз. автономным автоматом, или генератором, если функция переходов не зависит от букв входного алфавита. Под поведением инициального автономного автомата 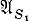принято понимать сверхслово

ψ (s₁)ψ (φ (s₁))ψ (φ² (s₁))..., где φ^{n + 1} (s) = φ (φⁿ (s)). Эта последовательность является периодической с нек-рым предпериодом.

А. к. 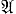наз. переходной системой, если B = S и для всякого s из S имеет место 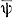(s, a) = s, или же если выходной алфавит В-пустой. Таким образом, переходная система полностью определяется тройкой (A, S, φ).

Понятия А. к. и функционирования А. к. могут быть определены различными эквивалентными способами (см. Автоматов способы задания, Автомата поведение). Широкое распространение получили так наз. канонические уравнения. Для произвольного слова α пусть α (t) обозначает t-ю букву слова α, а |α | - длину слова α. Тогда функционирование F А. к. 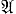состоит из всех тех и только тех троек слов (α, σ, β), к-рые удовлетворяют условиям: 1) |α | = |β | = |σ | - 1; 2) для всякого t такого, что 1 ≤ t ≤ |α |, имеют место равенства σ (t - 1) = φ (σ (t), α (t)), β (t) = ψ (σ (t), α (t)). Для определения поведения инициального А. к. 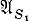необходимо добавить равенство σ (1) = s₁ . Совокупность этих равенств однозначно определяет поведение инициального А. к. и наз. обычно каноническими уравнениями. Канонич. уравнения широко используются в задачах анализа и синтеза автоматов.

Микроподход. Рассматривается множество элементов, состоящее из определенных выше А. к. с входными и

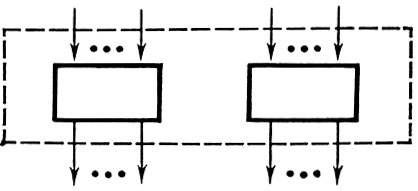
Рис. 1.

выходными алфавитами вида А_N, где А - конечный алфавит, одинаковый для всех элементов. Правила построения структурных А. к. из элементов описывают дозволенные соединения (отождествления) входов и выходов, а также определяют множества входов и выходов, получаемых А. к.

Важнейшим примером таких А. к. являются логические сети (л. с). Ниже приводится один из вариантов этого понятия. В рассматриваемом случае А = = {0, 1} и элементами являются так наз. функциональные элементы (ф. э.), представляющие собой А. к. с одним состоянием, а также специальные автоматы Мура, наз. задержками. Последние характеризуются тем, что они имеют два состояния, к-рые обычно обозначаются буквами 0 и 1 входного алфавита, причем функции переходов и выходов удовлетворяют условиям: φ (а, b) = b, ψ (а) = а. Поскольку ф. э. имеет только одно состояние, то он полностью характеризуется функцией выходов ψ, являющейся в этом случае булевой функцией от n аргументов, где n - число входов ф. э. Элементы являются исходными л. с, входы и выходы к-рых совпадают, соответственно, с входами и выходами элементов. Дальнейшее построение более сложных л. с. производится по следующим правилам.

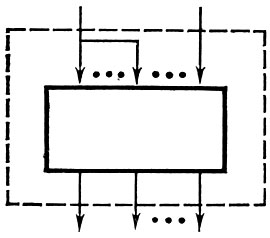
Рис. 2

1. Объединение двух л. с. есть л. с, входами и выходами к-рой являются, соответственно, входы и выходы объединяемых л. с. (рис. 1).

2. Результат отождествления любых двух входов л. с. является л. с, выходы к-рой совпадают с выходами исходной л. с, а входами служат все входы исходной л. с, кроме одного из отождествленных (рис. 2).

3. Результат отождествления выхода одной л. с. с входом другой л. с. есть л. с. Ее входами являются все входы первой л. с. и те входы второй л. с. к-рые не отождествлялись с выходом первой л. с; ее выходами являются все выходы обеих л. с. (рис. 3).

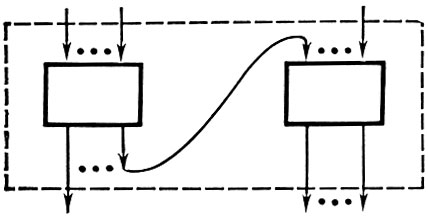
Рис. 3

4. Результат отождествления выхода л. с. являющегося выходом задержки, с произвольным входом этой же л. с. есть л. с, входы к-рой - все входы исходной л. с, кроме отождествленного, а выходы - все выходы исходной л. с. (рис. 4). (При нек-рых ограничениях это правило может быть применимо и к выходам, не являющимся выходами задержек.)

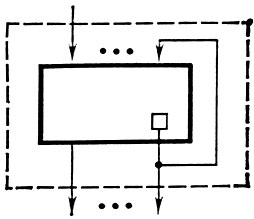
Рис. 4

5. В любой л. с. можно объявить выходами только часть выходов, определенных согласно правилам 1-4. Л. с, получаемые из ф. э. с помощью правил 1, 2, 3, 5, наз. обычно схемами из ф. э.

Функционирование л. с. содержательно можно описать следующим образом. Пусть в момент t всем входам л. с. приписаны входные буквы и определены состояния задержек. Тогда в этот же момент всем входам и выходам элементов л. с, в частности всем выходам л. с, будут приписаны буквы в соответствии со следующими правилами. Если входам ф. э. с выходной функцией ψ (х₁, ..., х_n) приписаны, соответственно, буквы a_i1, ..., a_in, то его выходу в этот же момент будет приписана буква, являющаяся значением ψ (a_i1, ..., a_in). Если задержка находится в момент t в состоянии а, то в этот же момент ее выходу приписывается буква а. Отождествленным входам и выходам приписываются одинаковые буквы. Далее, в момент t + 1 состояния задержек определяются входными буквами в момент t, как было определено выше, т. е. φ (а, b) = b. Таким образом, при фиксированных начальных состояниях задержек л. с. определяет нек-рое отображение входных последовательностей в алфавите А^m в выходные последовательности в алфавите Аⁿ, где m, m ≥ 1, - число входов, а n, n ≥ 1, - число выходов л. с. Класс таких отображений совпадает с классом функций, реализуемых А. к. в первом смысле (т. е. с классом ограниченно детерминированных функций), поскольку описанное выше функционирование л. с. совпадает с функционированием А. к. (А^m, S, Аⁿ, φ, ψ), где m - число входов, n - число выходов л. с, S - декартово произведение множеств состояний всех задержек л. с; функция переходов φ является покоординатным применением функций переходов задержек, а функция выходов ψ определяется в соответствии с вышеописанным функционированием ф. э. и задержек.

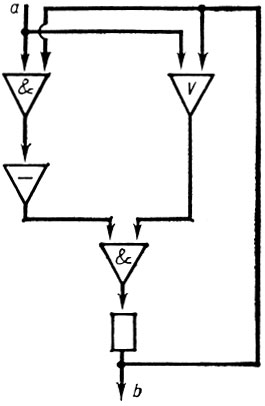
Рис. 5

Пусть, напр., элементами являются задержки (к-рые на рисунке изображаются прямоугольниками) и ф. э. с выходными функциями 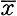, х ∨ у и х& у (треугольники с соответствующими символами функций). На рис. 5 изображена л. с, к-рая в тактовый момент t выдает выходную букву 1 в том и только в том случае, если среди входных букв в моменты 0, 1, 2, ..., t содержится нечетное число букв 1 (задержка в начальный момент имеет состояние 0; буквами а и b обозначены, соответственно, вход и выход л. с). Если обозначить через s(t), a(t), b(t), соответственно, состояние, входную букву и выходную букву в момент t, то функционирование такой л. с. можно задать следующими канонич. уравнениями:

s(0) = 0, s(t + 1) = s(t) + a(t)(mod 2), b(t) = s(t).

При макроподходе этот автомат можно представить в виде (A, S, А, φ, ψ), где А = S = {0, 1}, φ (s, a) = s + a(mod 2) и ψ (s, a) = s.

Понятие А. к. явилось отправным пунктом современной автоматов теории, изучающей также различные модификации и обобщения этого понятия.

Лит. : [1] Автоматы. Сб. статей, под ред. К. Э. Шеннона и Дж. Маккарти, пер. с англ., М.. 1956; [2] Глушков В. М., Синтез цифровых автоматов, М., 1962; [3] Кобринский Н. Е., Трахтенброт Б. А., Введение в теорию конечных автоматов, М., 1962.

В. Б. Кудрявцев, Ю. И. Янов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.