
АВТОМАТ
Расстановка ударений: АВТОМА`Т
АВТОМАТ - управляющая система, являющаяся автоматом конечным или некоторой его модификацией, полученной путем изменения компонент или функционирования. Основное понятие - конечный А. - возникло в середине 20 в. в связи с попытками описать на математическом языке функционирование нервных систем, универсальных вычислительных машин и других реальных А., предпринятыми впервые У. Мак-Каллоком и У. Питтсом (W. McCulloch, W. Pitts, 1943), С. К. Клини (S. С. Kleene, 1951), А. Бёрксом и Дж. Райтом (A. W. Burks, 1954, J. Wright) и др. Характерной особенностью такого описания является дискретность соответствующих математических моделей и конечность областей значений их параметров, что приводит к понятию конечного А. При этом внешние воздействия, реакции и состояния рассматриваются как буквы трех алфавитов, наз., соответственно, входным алфавитом, выходным алфавитом и алфавитом состояний. Тогда законы их взаимодействия могут быть заданы двумя функциями - функцией переходов и. функцией выходов, отображающими пары «состояние - входная буква» в состояния и выходные буквы, соответственно. В каждый из моментов дискретного времени устройство, находящееся в определенном состоянии, воспринимает входной сигнал - букву входного алфавита, выдает выходной сигнал - букву выходного алфавита, определяемую функцией выходов, и переходит в новое состояние, определяемое функцией переходов. Наряду с понятием конечного А. рассматриваются различные его обобщения и модификации, отражающие те или иные особенности реальных устройств. Для конечного A. (A, S, В, φ, ψ) существующие модификации можно разбить на следующие три основные группы. К первой группе относятся А., у которых некоторые из алфавитов A, S или В бесконечны, в связи с чем такие А. наз. бесконечными. Ко второй группе относятся А., у к-рых вместо функций φ и ψ допускаются произвольные отношения или случайные функции. Таковы частичные, недетерминированные, вероятностные и другие А. К третьей группе относятся А. со специфич. множествами входных объектов. Таковы А. с переменной структурой, А. над термами (см. Автоматов алгебраическая теория). Существуют А., принадлежащие одновременно разным группам; напр., А. нечеткие относятся ко всем трем группам. Наряду с этим большую роль играют специальные подклассы конечных А. ; например, А. без памяти, автономные, обратимые А. и т. д. Кроме того, использование понятий и методов из других разделов математики также приводит к появлению специфич. классов А. и связанных с ними задач. Напр., при применении алгебраич. средств возникают понятия А. над термами, линейного, группового, свободного и других А. (см. Автоматов алгебраическая теория); вопросы теории кодирования порождают понятия самонастраивающихся, обратимых А. и др. (см. также Автомат вероятностный). Для структурных А. также имеется целый ряд обобщений, сводящихся в основном к допущению бесконечных сетей и возможности изменения связей между элементами в процессе функционирования. Таким образом возникает понятие растущего А. Ниже описываются основные модификации и подклассы конечных А., а также их важнейшие свойства.
Макроподход. 1. А. бесконечные (первая группа) отличаются от А. конечных только тем, что их алфавиты А, В или S (входной, выходной и множество состояний) могут быть бесконечными. Большинство понятий и задач, связанных с конечными А., естественно распространяются на бесконечные А. Увеличение мощности алфавитов расширяет вычислительные возможности А. Так, напр., если конечные А. реализуют ограниченно-детерминированные функции, то с помощью бесконечных А. можно реализовать любую детерминированную функцию. Более того, с помощью бесконечных А. может быть описано функционирование любых А* и машин. Вместе с тем большая общность понятия бесконечного А. снижает его содержательное значение, так что в основном изучаются лишь специальные подклассы бесконечных А., связанные с конкретными моделями управляющих систем.
2. Недетерминированные А. и асинхронные А. (вторая группа). Формально недетерминированный А. определяется как система (A, S, В, χ), где A, S, В - алфавиты, имеющие прежний смысл, a χ ⊆ S × A × S × B-отношение переходов - выходов. В том случае, когда отношение χ является функцией, отображающей S × A в S × B, недетерминированный А. наз. детерминированным А. и фактически совпадает с конечным А., поскольку в этом случае функцию χ можно рассматривать как пару функций φ, ψ, отображающих S × A в S и В, соответственно. В отличие от конечного А., инициальный недетерминированный A. 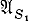 имеет несколько начальных состояний, образующих подмножество S1 множества S. Под поведением этого А.
имеет несколько начальных состояний, образующих подмножество S1 множества S. Под поведением этого А. 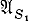 обычно понимают одно из следующих обобщений поведения конечного А.
обычно понимают одно из следующих обобщений поведения конечного А.
1) Вместо функции f автомат 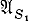 реализует отношение f', состоящее из всех пар слов (а1 ...аn, b1 ...bn) ∈ A* × B* таких, что найдутся состояния s1, s2, ..., sn + 1, для к-рых s1 ∈ S1 и для любого i = 1, 2, ..., n имеет место (si ai si + 1 bi)) ∈ χ. Класс отношений, реализуемых инициальным недетерминированным А., совпадает с классом ограниченно-детерминированных отношений (см. Ограниченно-детерминированная функция).
реализует отношение f', состоящее из всех пар слов (а1 ...аn, b1 ...bn) ∈ A* × B* таких, что найдутся состояния s1, s2, ..., sn + 1, для к-рых s1 ∈ S1 и для любого i = 1, 2, ..., n имеет место (si ai si + 1 bi)) ∈ χ. Класс отношений, реализуемых инициальным недетерминированным А., совпадает с классом ограниченно-детерминированных отношений (см. Ограниченно-детерминированная функция).
2) Инициальный недетерминированный A. 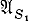 , у к-рого выделено множество S' заключительных состояний, а алфавит В пуст (т. е. χ ⊆ S × A × S), представляет событие LS', состоящее из всех слов а1 ...аn ∈ А* таких, что найдутся состояния s1, s2, ..., sn + 1, для к-рых s1 ∈ S1, sn + 1 ∈ S' и для любого i = l, 2, n имеет место (si ai si + 1) ∈ χ. Класс событий, представимых A.
, у к-рого выделено множество S' заключительных состояний, а алфавит В пуст (т. е. χ ⊆ S × A × S), представляет событие LS', состоящее из всех слов а1 ...аn ∈ А* таких, что найдутся состояния s1, s2, ..., sn + 1, для к-рых s1 ∈ S1, sn + 1 ∈ S' и для любого i = l, 2, n имеет место (si ai si + 1) ∈ χ. Класс событий, представимых A. 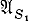 , совпадает с классом регулярных событий, т. е. относительно такого поведения недетерминированные А. эквивалентны конечным А. В то же время большая общность понятия недетерминированного А. проявляется в том, что для представления одного и того же события с помощью недетерминированного А. и конечного А. требуется различное число состояний. Существуют события, представимые недетерминированными А. с m состояниями и представимые конечными А. с 2m состояниями, причем никакие конечные А. с меньшим числом состояний не представляют эти события.
, совпадает с классом регулярных событий, т. е. относительно такого поведения недетерминированные А. эквивалентны конечным А. В то же время большая общность понятия недетерминированного А. проявляется в том, что для представления одного и того же события с помощью недетерминированного А. и конечного А. требуется различное число состояний. Существуют события, представимые недетерминированными А. с m состояниями и представимые конечными А. с 2m состояниями, причем никакие конечные А. с меньшим числом состояний не представляют эти события.
Специальный подкласс недетерминированных А. образуют так наз. частичные А., у к-рых отношение χ является частичной функцией, отображающей множество S × A в S × B, и к-рые реализуют частичные ограниченно-детерминированные функции.
Термином «асинхронный А. » обычно обозначают один из двух следующих видов А. К первому относятся А. вида (A, S, В, φ, ψ), где функция выходов ψ отображает множество S × B в В* (у конечного А. ψ отображает S × B в В). Эти А. используются главным образом в теории кодирования. Ко второму виду относятся конечные А., функция переходов у к-рых обладает следующим свойством: φ (s, aa) = φ (s, а) для любых s и а. Эти А. также используются в теории кодирования и, кроме того, для моделирования нек-рых систем в технике и биологии.
3. А. с переменной структурой (третья группа) - это конечные А. 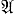 = (А × А, S, В, φ, ψ) с двумя входами, у к-рых зафиксирована нек-рая бесконечная последовательность α (сверхслово) в алфавите А. На первый вход такого А. подаются произвольные слова в алфавите А, а на второй - начала последовательности α той же длины. Тем самым накладывается ограничение на множество пар входных слов. Если А. с переменной структурой рассматривать как А. с одним первым входом (на к-рый могут подаваться любые слова в алфавите A), то его функции переходов и выходов будут зависеть от длины поданной части входного слова. Относительно поведения А. с переменной структурой эквивалентны бесконечным А. с конечными входным и выходным алфавитами и счетным множеством состояний.
= (А × А, S, В, φ, ψ) с двумя входами, у к-рых зафиксирована нек-рая бесконечная последовательность α (сверхслово) в алфавите А. На первый вход такого А. подаются произвольные слова в алфавите А, а на второй - начала последовательности α той же длины. Тем самым накладывается ограничение на множество пар входных слов. Если А. с переменной структурой рассматривать как А. с одним первым входом (на к-рый могут подаваться любые слова в алфавите A), то его функции переходов и выходов будут зависеть от длины поданной части входного слова. Относительно поведения А. с переменной структурой эквивалентны бесконечным А. с конечными входным и выходным алфавитами и счетным множеством состояний.
4. Нечеткие А. получаются как обобщение понятия конечного А. путем замены функций переходов и выходов нечеткими отношениями. Нечеткое подмножество множества М задается функцией, отображающей М в отрезок [0, 1]. Таким образом, роль функций переходов и выходов в нечетком А. играют функции, отображающие множества S × A × S и S × A × В в отрезок [0, 1], где S - множество состояний, А - входной алфавит, В - выходной алфавит. Для нечетких А. естественно обобщаются основные понятия и задачи, характерные для конечных А., в частности задачи представления нечетких событий и реализации нечетких отношений. Нечеткие А. являются математич. моделями нек-рых распознающих устройств и используются в задачах распознавания образов.
5. Специальные классы конечных А.
А. без памяти - это конечные А. с одним состоянием или А., эквивалентные им. Для таких А. каждая выходная буква полностью определяется входной буквой, поступившей в тот же момент. Эти А. часто наз. функциональными элементами и широко применяются в задачах синтеза А.
А. с конечным запоминанием, наз. иногда А. с конечной памятью, - это конечные А., любая выходная буква к-рых при любом исходном состоянии полностью определяется ограниченным отрезком входного слова, поступившим в предшествующие моменты. Минимальная длина таких отрезков для А. с конечным запоминанием с n состояниями не превосходит ½ n(n - 1), причем для нек-рых А. эта оценка достигается. А. с конечным запоминанием наз. самонастраивающимся, если для нек-рого t выходная буква в любой момент τ ≥ t не зависит от исходного состояния. Эти А. используются в теории кодирования (см. Кодирование и декодирование), где обычно рассматривается модификация таких А., к-рая удовлетворяет указанному условию не для всех входных слов, а только для нек-рого подмножества их. А. с конечным запоминанием реализуются логич. сетями без обратных связей.
А. обратимые, или А. без потери информации, - это конечные А., реализующие взаимно однозначные функции. Эти А. также используются в теории кодирования.
Микроподход. Существует три вида обобщений структурных А., к-рые можно рассматривать как обобщенные логич. сети: 1) обобщенные логич. сети с неизменной структурой, у к-рых элементы и связи между ними не меняются в процессе функционирования; 2) обобщенные логич. сети с изменяющейся структурой; 3) обобщенные логич. сети из объемных элементов и связей. Ниже приведены основные классы таких А.
1. Обобщенные логич. сети с неизменной структурой. К ним относятся мозаичные структуры и итеративные сети, являющиеся конечными фрагментами мозаичных структур с аналогичным кругом задач.
Мозаичные структуры представляют собой бесконечные соединения переходных систем (А, S, φ) (т. е. конечных А. вида (A, S, S, φ, φ), где функция выходов совпадает с функцией переходов, а выходной алфавит - с множеством состояний). Такие системы помещаются в целочисленные точки n-мерного пространства, причем для каждой точки определено конечное множество целочисленных точек, называемое ее окрестностью. Входной алфавит переходной системы, помещенной в данную точку, представляет собой декартово произведение множеств состояний переходных систем, помещенных в точки ее окрестности.
Мозаичную структуру можно рассматривать как бесконечный А., входной и выходной алфавиты, а также множество состояний к-рого равны и являются бесконечным декартовым произведением множеств состояний всех переходных систем, содержащихся в ней. Это позволяет сводить многие задачи для мозаичных структур к задачам для бесконечных А. К числу специфич. задач для мозаичных структур относится моделирование эффективных процедур и, в частности, вычислительных процессов. Иногда рассматривают мозаичные структуры, в к-рых вместо переходных систем используются произвольные А.
Важный класс мозаичных структур образуют однородные структуры. В случае, когда все переходные системы одинаковы и окрестность любой точки получается параллельным переносом нек-рой окрестности, мозаичная структура наз. однородной структурой. При этом обычно предполагается, что имеется нек-рое «устойчивое» состояние переходной системы, к-рое сохраняется, когда входной буквой является кортеж, каждый член к-рого совпадает с этим состоянием. Характерными задачами для однородных структур являются задачи о самовоспроизведении и «райских садах».
В каждый момент состояния переходных систем, помещенных в точках целочисленной решетки, образуют как бы пространственную мозаичную картину, наз. обычно конфигурацией. Конфигурация, содержащая только конечное множество переходных систем, находящихся в состояниях, отличных от устойчивого (возбужденная часть), наз. конечной. Задача о самовоспроизведении состоит в выяснении существования конечных конфигураций, к-рые в процессе функционирования однородной системы переходят в конфигурации, возбужденная часть к-рых представляет собой многократно повторенную возбужденную часть исходной конфигурации. «Райским садом» наз. конфигурация, к-рая не может возникнуть из конфигураций, отличных от нее. Задача о «райских садах» состоит в выяснении существования «райских садов» для заданной однородной структуры.
2. Обобщенные логич. сети с изменяющейся структурой. Существуют разные виды таких логич. сетей. К числу наиболее общих из них относятся мозаичные структуры, у к-рых в процессе функционирования меняются как окрестности элементов, так и сами элементы. Примером такой обобщенной логич. сети может служить одномерная структура, имитирующая работу Тьюринга машины со входом. Одному из узлов одномерной решетки в этом случае соответствует управляющее устройство, а остальным - ячейки ленты, рассматриваемые как переходные системы, входными буквами и состояниями к-рых являются буквы рабочего алфавита машины Тьюринга. Коммутация определяется положением головки.
Другим видом обобщенных логич. сетей с изменяющейся структурой являются так наз. растущие А. Они представляют собой однородные структуры, в к-рых возбужденная часть растет в процессе функционирования. Существует несколько моделей таких А., отражающих различные особенности реальных устройств.
3. Обобщенные логич. сети из объемных элементов отличаются тем, что элементарным А. и связям между ними приписывается определенный объем, в связи с чем возникает задача синтеза А., имеющих минимальный объем.
Термин «А. » употребляется также в таких понятиях, как двусторонний, многоленточный, многоголовочный, линейно ограниченный и т. п. А., к-рые фактически являются модификациями машин Тьюринга. Более того, иногда в понятие А. включают все абстрактные машины.
Лит. : [1] Мак-Каллок У., Питтс В., в сб. : Автоматы, М., 1956, с. 362-84; [2] Клини С, там же, с. 15-67; 13] Бёркс А., Райт Д., в кн. : Кибернетический сборник, в. 4, М., 1962, с. 33-57; [4] Глушков В. М., «Успехи матем. наук», 1961, т. 16, № 5, с. 3-62; 1962, т. 17, № 2; [5] Рабин М. О., Скотт Д., в кн. : Кибернетический сборник, в. 4, М., 1962, с. 58-91: [6] Zadеh L. A., «J. Math. Anal. and Appl. », 1968, v. 23, № 2, p. 421-427; [7] Аладьeв В. З., К теории однородных структур, Тал., 1972.
В. Б. Кудрявцев, Ю. И. Янов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'