АБСОЛЮТНОЕ ЗНАЧЕНИЕ

Расстановка ударений: АБСОЛЮ`ТНОЕ ЗНАЧЕ`НИЕ

АБСОЛЮТНОЕ ЗНАЧЕНИЕ на теле - отображение φ тела K в множество ℝ действительных чисел, удовлетворяющее условиям:

1) φ (х) ≥ 0 и φ (х) = 0 тогда и только тогда, когда х = 0;

2) φ (x ⋅ y) = φ (х) ⋅ φ (у);

3) φ (x + y) ≤ φ (x) + φ (у).

Отсюда φ (1) = φ (- 1) = 1, φ (х^{- 1}) = φ^{- 1} (x).

А. з. часто обозначается |х| вместо φ (х). А. з. наз. также нормой, мультипликативным нормированием. А. з. могут рассматриваться на любом кольце со значениями в линейно-упорядоченном кольце [4] (см. также Нормирование).

Примеры А. з. Если K = ℝ - поле действительных чисел, то |x| = mах {х, - х} является абсолютной величиной, или модулем, числа х ∈ ℝ. Аналогично, если К-поле ℂ комплексных чисел или тело |Н| кватернионов, то 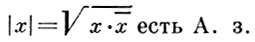Подполя этих полей также снабжаются индуцированным А. з. Любое тело имеет тривиальное А. з. :

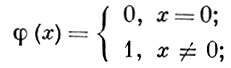
конечные поля и их алгебраич. расширения имеют только такие А. з.

Примеры А. з. другого типа доставляют логарифмич. нормирования тела К: если v-нормирование K со значениями в группе ℝ и а - действительное число, 0 < а < 1, то φ (х) = а^v(x) является А. з. Например, если K = ℚ, a v_p есть р-адическое нормирование поля О, то |x|_p = (1/p)^{v_p (x)} называется р-адическим А. з., или р-адической нормой. Эти А. з. удовлетворяют более сильному, чем 3), условию 4) φ (x + y) ≤ max{φ (х), φ (y)}.

А. з., удовлетворяющие условию 4), наз. ультраметрическими А. з., или неархимедовыми А. з. (в отличие от архимедовых А. з., не удовлетворяющих этому условию). Они характеризуются тем, что φ (n ⋅ 1) ≤ 1 для всех целых n. Все А. з. тела характеристики р > 0 являются ультраметрич. А. з. Все ультраметрич. А. з. получаются из нормирований указанным выше способом: φ = а^v(x) (и обратно, за нормирование всегда можно взять - logφ).

А. з. φ определяет метрику на K, если за расстояние между х и у принять φ (х - у), и тем самым определяет топологию на К. Так, топология любого локально компактного тела определяется нек-рым абсолютным значением. А. з. φ₁ и φ₂ наз. эквивалентными, если они определяют одну топологию; в этом случае существует такое λ > 0, что φ₁ (х) = φ₁ (х)^λ для всех х ∈ К.

Структура всех архимедовых А. з. дается теоремой Островского: если φ - архимедово А. з. на теле К, то существует такой изоморфизм К на нек-рое всюду плотное подтело тела ℝ, ℂ или |Н|, что φ эквивалентно А. з., индуцированному с ℝ, ℂ или |Н|.

Любое нетривиальное А. з. поля ℚ рациональных чисел эквивалентно либо р-адическому А. з. |  |р (где р-простое число), либо обычной абсолютной величине. При этом для любого рационального числа r ∈ ℚ

|r|∏_p |r|_p = 1.

Аналогичная формула имеет место и для полей алгебраич. чисел (см. [2], [3]).

Если φ - нек-рое А. з. тела K, то К может быть вложено, при помощи классич. процесса пополнения, в тело K_φ, полное относительно А. з., продолжающего φ (см. Полное топологическое пространство). Одним из основных современных методов изучения полей является вложение поля К в прямое произведение П_φ K_φ ; пополнений K_φ поля К по всем А. з. (см. Адель); поле К плотно лежит в П_φ K_φ : именно, если φ₁, φ₂, ..., φ_n - нетривиальные неэквивалентные А. з. на поле К, а₁, ..., а_n - элементы из K и ε > 0, то существует такое а ∈ К, что φ_i (а - а_i) < ε для всех i (теорема аппроксимации для А. з.).

А. з. поля К может быть продолжено (вообще говоря неоднозначно) на любое алгебраич. расширение поля К. Если К полно относительно А. з. φ, a L есть расширение К степени n, то продолжение φ на L единственно и задается формулой 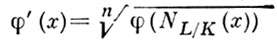для х ∈ L.

Лит. : [1] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971; [2] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [3] Ленг С., Алгебра, пер. с англ., М., 1968; [4] Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973; [5] Алгебраическая теория чисел, пер. с англ., М., 1969.

В. И. Данилов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.