АБСОЛЮТНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ

Расстановка ударений: АБСОЛЮ`ТНО ИНТЕГРИ`РУЕМАЯ ФУ`НКЦИЯ

АБСОЛЮТНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ - функция, у к-рой интегрируема ее абсолютная величина. Если функция f(x) интегрируема по Риману на отрезке [a, b], а < b, то ее абсолютная величина интегрируема по Риману на этом отрезке и

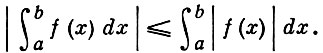
Аналогичное утверждение справедливо для функции n переменных, интегрируемой по Риману на кубируемой области n-мерного евклидова пространства. Обратное утверждение для функции, интегрируемых по Риману, не справедливо: функция f(x), равная 1 для рациональных x и -1 для иррациональных, не интегрируема по Риману, а ее абсолютная величина интегрируема. Для функций, интегрируемых по Лебегу, дело обстоит иначе: функция f(x) интегрируема по Лебегу (суммируема) на измеримом множестве Е n-мерного пространства тогда и только тогда, когда на этом множестве интегрируема по Лебегу ее абсолютная величина, при этом справедливо неравенство:

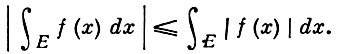
В случае несобственных одномерных интегралов в смысле Римана или Лебега по промежутку [а, b), a < b ≤ + ∞ (при условии, что функция f(x) интегрируема по Риману или, соответственно, по Лебегу на любом отрезке [а, η], а < η < b) из существования несобственного интеграла от абсолютной величины функции

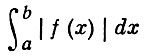
следует и существование интеграла

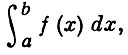
но не наоборот (см. Абсолютно сходящийся несобственный интеграл). При этом, если существует несобственный интеграл

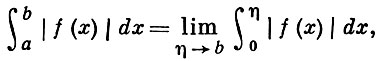
то функция f(x) интегрируема по Лебегу на промежутке [a, b) и несобственный интеграл от нее равен интегралу Лебега.

В случае функций многих переменных (число к-рых n > 1) несобственные интегралы обычно определяются таким образом, что существование несобственного интеграла от абсолютной величины функции равносильно существованию несобственного интеграла от самой функции.

Пусть значения функции f(x) принадлежат нек-рому банахову пространству с нормой || ⋅ ||. Тогда функция f(х) наз. абсолютно интегрируемой на измеримом множестве Е, если существует интеграл

||∫_E f(x)dx; || ≤ ∫_E ||f(x)||dx;

при этом, если функция f(х) интегрируема на Е, то

∫_E ||f(x)||dx;

Лит. : [1] Ильин В. А., Позняк Э. Г., Основы математического анализа, ч. 1, 3 изд., М., 1971; [2] Кудрявцев Л. Д., Математический анализ, т. 1, 2 изд., М., 1973; [3] Никольский С. М., Курс математического анализа, 2 изд., т. 1, М., 1975; [4] Шварц Л., Анализ, пер. с франц, т. 1, М., 1972.

Л. Д. Кудрявцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.