
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ
Расстановка ударений: АБСОЛЮ`ТНАЯ НЕПРЕРЫ`ВНОСТЬ
АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ - 1) А. н. интеграла - свойство неопределенного интеграла (Лебега). Пусть функция f μ - интегрируема на множестве Е. Интеграл от f на μ-измеримых подмножествах e ⊂ E является абсолютно непрерывной функцией (см. ниже - п. 3) множества относительно меры μ, т. е. для всякого ε > 0 найдется такое δ > 0, что интеграл |∫e fdμ | < ε для любого множества е с μ (е) < δ. В общем случае интеграл по конечно аддитивной функции множества μ как со скалярными, так и с векторными f или μ, есть абсолютно непрерывная функция.
А. П. Терехин, В. Ф. Емельянов.
2) А. н. меры - понятие теории меры. Мера ν наз. абсолютно непрерывной относительно меры μ, если ν - абсолютно непрерывная функция множества относительно μ. Так, пусть ν - конечная мера, заданная с μ на нек-рой фиксированной σ-алгебре G; тогда ν абсолютно непрерывна относительно μ, если из μ (A) = 0, A ∈ G, следует ν (A) = 0. Обобщенная конечная мера ν абсолютно непрерывна относительно обобщенной меры μ, если ν (A) = 0 как только |μ |(A) = 0, где |μ | - полная вариация μ.
А. П. Терехин.
3) А. н. функции - усиление понятия непрерывности. Функция f(x), определенная на отрезке [а, b], наз. абсолютно непрерывной, если для любого ε > 0, существует такое δ > 0, что для любой конечной системы попарно непересекающихся интервалов (ak, bk) ⊂ (a, b), k = 1, 2, ..., n, для которой
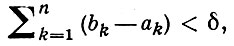
справедливо неравенство
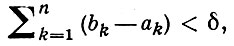
Всякая абсолютно непрерывная на отрезке функция непрерывна на этом отрезке; обратное неверно, напр. функция 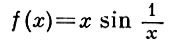 при 0 < х ≤ 1 и f(0) = 0, будучи непрерывной на отрезке [0, 1], не является на нем абсолютно непрерывной. Если в определении абсолютно непрерывной функции, отбросить требование пустоты попарных пересечений интервалов (ak, bk), то функция будет удовлетворять более сильному условию - Липшица условию с нек-рой постоянной.
при 0 < х ≤ 1 и f(0) = 0, будучи непрерывной на отрезке [0, 1], не является на нем абсолютно непрерывной. Если в определении абсолютно непрерывной функции, отбросить требование пустоты попарных пересечений интервалов (ak, bk), то функция будет удовлетворять более сильному условию - Липшица условию с нек-рой постоянной.
Если функции f(x) и g(x) абсолютно непрерывны, то абсолютно непрерывны и их сумма, разность и произведение, а если g(x) не обращается в нуль, то и частное f(x)/g(x). Суперпозиция двух абсолютно непрерывных функций может и не быть абсолютно непрерывной. Однако, если функция f(x) абсолютно непрерывна на отрезке [а, b] и А ≤ f(х) ≤ B, х ∈ [а, b], а функция F(у) удовлетворяет условию Липшица на отрезке [А, В], то сложная функция F[f(x)] абсолютно непрерывна на отрезке [а, b). Если абсолютно непрерывная на [а, b] функция f(x) монотонно возрастает, а функция F(y) абсолютно непрерывна на отрезке [f(a), f(b)], то функция F[f(x)] также абсолютно непрерывна на [а, b].
Абсолютно непрерывная функция отображает множество меры нуль в множество меры нуль, а измеримое множество в измеримое. Всякая непрерывная функция с конечной вариацией, отображающая каждое множество меры нуль в множество меры нуль, является абсолютно непрерывной функцией. Всякая абсолютно непрерывная функция может быть представлена как разность двух абсолютно непрерывных неубывающих функций.
Абсолютно непрерывная на отрезке [а, b] функция f(х) имеет на нем конечную вариацию и почти в каждой его точке - конечную производную f'(х), суммируемую на этом отрезке, причем
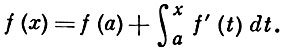
Если производная абсолютно непрерывной функции почти всюду равна нулю, то сама функция постоянна. С другой стороны, для любой суммируемой на отрезке [а, b] функции φ (х) функция 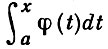 абсолютно непрерывна на этом отрезке. Поэтому класс абсолютно непрерывных на данном отрезке функций совпадает с классом функций, представимых в виде неопределенного интеграла Лебега: интеграла Лебега с переменным верхним пределом от нек-рой суммируемой функции плюс постоянная.
абсолютно непрерывна на этом отрезке. Поэтому класс абсолютно непрерывных на данном отрезке функций совпадает с классом функций, представимых в виде неопределенного интеграла Лебега: интеграла Лебега с переменным верхним пределом от нек-рой суммируемой функции плюс постоянная.
Если f(x) абсолютно непрерывна на [а, b], то ее полная вариация равна:
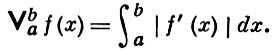
Понятие А. н. обобщается как на случай функций многих переменных, так и на случай функций множеств (см. ниже - п. 4).
Лит. : [1] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976; [2] Смирнов В. И., Курс высшей математики, т. 5, М., 1959.
Л. Д. Кудрявцев.
4) А. н. функции множества - понятие, употребляемое обычно применительно к счетно аддитивным функциям, определенным на σ-кольце S подмножеств множества X. Так, если μ, ν - две определенные на S счетно аддитивные функции со значениями из расширенной числовой прямой [- ∞, ∞], то ν абсолютно непрерывна относительно μ. (символически это записывается в виде ν ≤ μ), если |μ |(Е) = 0 влечет ν (E) = 0 (здесь |μ | - полная вариация μ :
|μ | = μ+ + μ-, μ+ = sup {μ (F): E ⊃ F ∈ S}, μ- = - inf {μ (F): E ⊃ F ∈ S},
μ+ и μ- - меры, наз. положительной и отрицательной вариациями μ ; по теореме Жордана-Хана μ = μ+ - μ- . Оказывается, что соотношения 1) ν ≤ μ, 2) ν+ ≤ μ, ν- ≤ μ, 3) |ν | ≤ |μ | равносильны. Если мера ν конечна, то ν ≤ μ, тогда и только тогда, когда для любого ε > 0 существует δ > 0 такое, что |μ | < δ влечет |ν | < ε. В силу Радона-Никодима теоремы, если μ, ν - вполне σ-конечны (т. е, X ∈ S и существует последовательность {Еn}, n = 1, 2, ..., такая, что
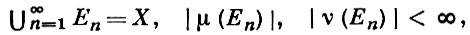
и ν ≤ μ), то на X существует конечная измеримая функция f такая, что
ν (E) = ∫E fdμ, E ∈ S.
Обратно, если μ вполне σ-конечна и интеграл ∫ fdμ имеет смысл, то ∫E fdμ как функция множества Е абсолютно непрерывна по μ. Если μ и ν вполне σ-конечные меры на (X, S), то существуют однозначно определенные вполне σ-конечные меры ν1 и ν2 такие, что ν = ν1 + ν2, ν1≪ν, и ν2 сингулярна относительно μ, (т. е. существует множество Е∈S такое, что |ν2 |(А) = 0, |μ |(Х\А) = 0) (теорема Лебега). Мера, определенная на борелевских множествах конечномерного евклидова пространства (или, более общим образом, локально компактной группы), называется абсолютно непрерывной, если она абсолютно непрерывна относительно меры Лебега (меры Хаара). Неотрицательная мера μ на борелевских множествах действительной прямой абсолютно непрерывна тогда и только тогда, когда отвечающая ей функция распределения F(х) = μ {(- ∞, х)} абсолютно непрерывна (как функция действительного переменного). Понятие А. н. функций множества может быть определено и для конечно аддитивных функций, и для функций с векторными значениями.
Лит. : [1] Xалмош П., Теория меры, пер. с англ., М., 1953; [2] Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969.
В. В. Сазонов.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'