АБЕЛЯ-ПУАССОНА МЕТОД СУММИРОВАНИЯ

Расстановка ударений: А`БЕЛЯ-ПУАССО`НА МЕ`ТОД СУММИ`РОВАНИЯ

АБЕЛЯ-ПУАССОНА МЕТОД СУММИРОВАНИЯ - один из методов суммирования рядов Фурье. Ряд Фурье функции f(x) ∈ L [0, 2π] суммируется методом Абеля-Пуассона в точке φ к числу S, если

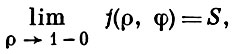
где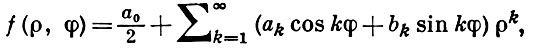

(*)

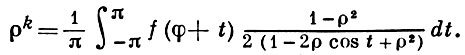
Если f(x) ∈ L (0, 2π), то интеграл в правой части есть гармонич. функция для |z| = |ρ e^iφ | < 1 и, как показал С. Пуассон (S. Poisson), является решением задачи Дирихле для круга. В связи с этим Абеля метод суммирования в применении к рядам Фурье наз. А.-П. м. с, а интеграл (*) - Пуассона интегралом.

Если (ρ, φ) - полярные координаты точки внутри круга радиуса 1, то можно рассматривать предел функции f(ρ, φ), когда точка (ρ, φ) стремится к точке на окружности не по радиальному, но и не по касательному и даже произвольному пути. Так, имеет место теорема Фату: если функция f(x) принадлежит L [0, 2π] и непрерывна в точке φ₀, то

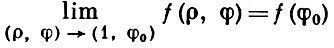
независимо от способа стремления точки М(ρ, φ) к точке Р(1, φ₀) при условии, что она остается внутри круга радиуса 1.

Лит. : [1] Бари Н. К., Тригонометрические ряды, М., 1961.

А. А. Захаров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.