АБЕЛЯ ТЕОРЕМА

Расстановка ударений: А`БЕЛЯ ТЕОРЕ`МА

АБЕЛЯ ТЕОРЕМА - 1) А. т. об алгебраических уравнениях: ни для какого n, большего или равного пяти, нельзя указать формулу, к-рая выражала бы корни любого уравнения n-й степени через его коэффициенты при помощи радикалов. Найдена Н. Абелем в 1824 (см. [1]). А. т. может быть получена также как следствие Галуа теории, из к-рой вытекает и более общее утверждение: для любого n ≥ 5 существуют алгебраич. уравнения с целыми коэффициентами, корни к-рых не выражаются через радикалы из рациональных чисел. Современную формулировку А. т. для уравнений над произвольным полем см. Алгебраическое уравнение.

2) А. т. для степенных рядов: если степенной ряд

(*)

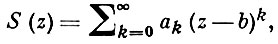
где a_k, b, z - комплексные числа, сходится при z = z₀, то он абсолютно и равномерно сходится в любом круге |z - b| ≤ ρ радиуса ρ < |z₀ - b| с центром в точке b. Установлена Н. Абелем [2]. Из этой теоремы вытекает, что существует число R ∈ [0, ∞], обладающее тем свойством, что при |z - b| < R ряд сходится, а при |z - b| > R расходится. Это число R наз. радиусом сходимости ряда (*), а круг |z - b| < R наз. кругом сходимости ряда (*).

3) А. т. о непрерывности: если степенной ряд (*) сходится в точке z₀ границы круга сходимости, то он представляет собой непрерывную функцию в любом замкнутом треугольнике Т с вершинами z₀, z₁, z₂, где z₁, z₂ лежат внутри круга сходимости. В частности,

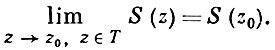
Этот предельный переход всегда можно осуществить по радиусу: на всем радиусе круга сходимости, соединяющем точки b и z₀, ряд (*) будет сходиться равномерно. Эта теорема используется, в частности, для вычисления суммы степенного ряда, сходящегося в точках на границе круга сходимости.

4) А. т. для рядов Дирихле: если Дирихле ряд

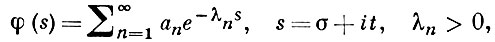
сходится в точке s₀ = σ₀ + it₀, то он сходится в полуплоскости σ > σ₀ и сходится равномерно внутри любого угла |arg(s - s₀)| ≤ θ < π /2. Является обобщением А. т. для степенных рядов (достаточно взять λ_n = n и обозначить e^{- S} = z). Из теоремы следует, что область сходимости ряда Дирихле - нек-рая полуплоскость σ > с, где с - абсцисса сходимости ряда.

Для обыкновенного ряда Дирихле (когда λ_n = ln n) с известной асимптотикой для сумматорной функции A_n = a₁ + a₂ + ... + a_n коэффициентов ряда справедлива следующая теорема: если

А_n = Вn^S1 (ln n)^α + O(n^β),

где В, s₁, α - комплексные числа, β - действительное число, σ₁ - 1 < β < σ₁, то ряд Дирихле сходится при σ₁ < σ, функция φ (s) регулярно продолжается на полуплоскость β < σ, исключая точку s = s₁, причем

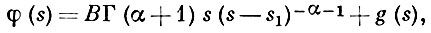
если α ≠ - 1, - 2, ...,

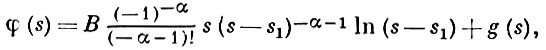
если α = - 1, - 2,... Здесь g(s) - регулярная при σ > β функция.

Напр., дзета: функция Римана ζ (s) (А_n = n, В = 1, s₁ = 1, α = 0, β > 0) регулярна по крайней мере в полуплоскости σ > 0, исключая точку s = 1, в к-рой она имеет полюс 1-го порядка с вычетом, равным 1. Эта теорема допускает различные обобщения. Так, если

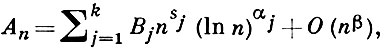
где B_j, s_j, α_j (1 ≤ j ≤ k) - любые комплексные числа, и σ_k - 1 < β < σ_k <... < σ₁, то ряд Дирихле сходится при σ > σ₁, φ (s) регулярен в области σ > β, исключая точки s₁, s₂, ..., s_k, в к-рых он имеет алгебраич. или логарифмич. особенности. Теоремы такого типа позволяют на основании асимптотики А_n получать определенные сведения о поведении ряда Дирихле в нек-рой полуплоскости.

Лит. : [1] Abel N., Oeuvres complètes, t. 1, Christiania, 1881; [2] eго же, «J. reine und angew. Math. », 1826, Bd 1, S. 311-99; [3] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.