АБЕЛЯ ПРИЗНАК

Расстановка ударений: А`БЕЛЯ ПРИ`ЗНАК

АБЕЛЯ ПРИЗНАК - 1) А. п. для числовых рядов: если сходится ряд

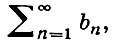
а числа а_n образуют монотонную ограниченную последовательность, то ряд

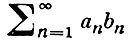
сходится.

2) А. п. для функциональных рядов: ряд

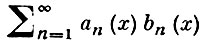
равномерно сходится на множестве X, если ряд

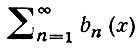
равномерно сходится на X, а функции а_n (х), n = 1, 2, ..., при каждом х ∈ X образуют монотонную последовательность, равномерно ограниченную на множестве X. Аналогично формулируется А. п. равномерной сходимости интегралов

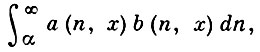
зависящих от параметра х ∈ X.

А. п. могут быть усилены (см., напр., Дедекинда признак). См. также Дирихле признак, Абеля преобразование.

Лит. : [1] Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, т. 1, 7 изд., М., 1969; [2] Кудрявцев Л. Д., Математический анализ, т. 1, 2 изд., М., 1973; [3] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., ч. 1, 2 изд., М., 1963.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.