АБЕЛЕВО МНОГООБРАЗИЕ

Расстановка ударений: А`БЕЛЕВО МНОГООБРА`ЗИЕ

АБЕЛЕВО МНОГООБРАЗИЕ - алгебраическая группа, являющаяся полным алгебраическим многообразием. Условие полноты накладывает сильные ограничения на А. м. Так, А. м. можно вложить в качестве замкнутого подмногообразия в проективное пространство, каждое рациональное отображение неособого многообразия в А. м. регулярно, групповой закон на A. м. всегда коммутативен.

Теория А. м. над полем комплексных чисел ℂ эквивалентна, по существу, теории абелевых функций, основы к-рой были заложены в работах К. Якоби (С. Jacobi), Н. Абеля (N. Abel) и Б. Римана (В. Riemann). Если ℂⁿ есть n-мерное векторное пространство, Г ⊂ ℂ_n - решетка (см. Дискретная подгруппа) ранга 2n, то факторгруппа Х = ℂⁿ /Г будет комплексным тором. Мероморфные функции на X отождествляются с мероморфными функциями на ℂ_n, инвариантными относительно решетки периодов Г. Если степень трансцендентности поля К мероморфных функций на X равна n, то X можно наделить структурой алгебраич. группы, единственной в силу компактности X и такой, что поле рациональных функций этой структуры совпадает с К. Получающиеся таким образом алгебраич. группы являются А. м. и всякое А. м. над полем ℂ имеет такой вид. Матрицу, задающую базис решетки Г, можно привести к виду (E|Z), где Е - единичная матрица, а Z - матрица порядка n×n. Комплексный тор Х = ℂⁿ /Г есть А. м. в том и только том случае, когда матрица Z симметрична и ее мнимая часть положительно определена. Необходимо отметить, что как вещественные группы Ли все многообразия X изоморфны, но это неверно для их аналитич. или алгебраич. структур, к-рые сильно меняются при деформации решетки Г. Рассмотрение матрицы периодов Z показывает, что это изменение носит аналитич. характер и это приводит к конструкции многообразия модулей всех абелевых многообразий данной размерности n. Его размерность равна ½ n(n + l) (см. Модулей проблема).

Теория А. м. над произвольным полем к принадлежит А. Вейлю (см. [1], [2]). Она имеет большое количество приложений как в самой алгебраич. геометрии, так и в других областях математики, особенно в теории чисел и теории автоморфных функций. Каждому полному алгебраич. многообразию можно сопоставить функториальным образом А. м. (см. Альбанезе многообразие, Пикара многообразие, Промежуточный якобиан). Эти конструкции представляют собой мощный метод изучения геометрич. структуры алгебраич. многообразий. Так, с их помощью было получено одно из решений Люрота проблемы. Другим приложением является доказательство гипотезы Римана для алгебраич. кривых над конечным полем. Именно для решения этой проблемы и была создана абстрактная теория А. м. Она послужила также одним из источников теории l-адических когомологий. Простейшим примером таких когомологий служит Тейта модуль А. м. Он является проективным пределом групп Х_lⁿ точек lⁿ-гo порядка при n → ∞. Определение структуры последних было одним из главных достижений теории А. Вейля. Именно, если m взаимно просто с характеристикой р поля k и k алгебраически замкнуто, то группа Х_m изоморфна 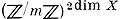. Ситуация в случае m = р гораздо сложнее и она привела к появлению таких понятий, как конечные групповые схемы, формальные группы и p-делимые группы. Изучение действия эндоморфизмов А. м., в частности Фробениуса эндоморфизма на его модуль Тейта, дает возможность доказать гипотезу Римана, а также является основным инструментом в теории комплексного умножения А. м. Другой круг вопросов, связанный с модулем Тейта, состоит в исследовании действия на нем группы Галуа замыкания основного поля. Отсюда возникли гипотезы Тейта и теория Тейта-Хонды, дающая для А. м. над конечными полями их описание в терминах модуля Тейта [5].

Интенсивно развивается изучение А. м. над локальными, в том числе р-адическими нолями. Аналог упомянутого выше представления А. м. в виде факторпространства ℂⁿ /Г (которое обычно наз. униформизацией) был построен над такими полями Д. Мамфордом (D. Mumford) и М. Рейно (М. Raynaud). В отличие от комплексного случая униформизуются не все А. м., а только имеющие редукцией по mod р мультипликативную группу [6]. Теория А. м. над глобальными (числовыми и функциональными) полями играет важную роль в диофантовой геометрии. Основной результат здесь - теорема Морделла-Вейля: группа рациональных точек А. м., определенного над конечным расширением поля рациональных чисел, конечно порождена.

Лит. : [1] Wеil A., Varietes abeliennes et courbes algebriques, P., 1948; [2] eго же, Sur les courbes algebriques et les varietes qui s'en deduisent, P., 1948; [3] Вейль А., Введение в теорию келеровых многообразий, пер. с франц., М., 1961; [4] Lang S., Abelian varietes, N. Y. - L., 1959; [5] Mамфоpд Д., Абелевы многообразия, пер. с англ., М., 1971; [6] Манин Ю. И., в сб. : Итоги науки и техники. Сер. Современные проблемы математики, т. 3, М., 1974, с. 5-93; [7] Серр Ж. П., Алгебраические группы и поля классов, пер. с франц., М., 1968; [8] 3игель К., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954.

Б. Б. Венков, А. Н. Паршин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.