АБЕЛЕВА ФУНКЦИЯ

Расстановка ударений: А`БЕЛЕВА ФУ`НКЦИЯ

АБЕЛЕВА ФУНКЦИЯ - обобщение эллиптической функции одного комплексного переменного на случай многих комплексных переменных. Мероморфная в комплексном пространстве ℂ^p, p ≥ 1 функция f(z) от р комплексных переменных z₁, z₂, ..., z_p z = (z₁, z₂, ..., z_p), наз. А. ф., если существуют 2р векторов - строк из ℂ^p

w_ν = (w_1ν, w_2ν, ..., w_pν), ν = 1, 2, ..., 2p,

линейно независимых над полем действительных чисел и таких, что f(z + w_ν) = f(z) для всех z ∈ ℂ^p, ν = l, 2, ..., 2р. Векторы w_ν наз. периодами, или системами периодов, А. ф. f(z). Все периоды А. ф. f(z) образуют абелеву группу Г по сложению, наз. группой периодов (или модулем периодов). Базис этой группы наз. базисом периодов А. ф., а также системой основных (или примитивных) периодов. А. ф. наз. вырожденной, если существует такое линейное преобразование переменных z₁, z₂, ..., z_p, к-рое переводит f(z) в функцию меньшего числа переменных; в противном случае f(z) наз. невырожденной А. ф. Вырожденные А. ф. характеризуются также тем, что они имеют бесконечно малые периоды, т. е. для любого числа ε > 0 можно найти период w_ν, для к-рого

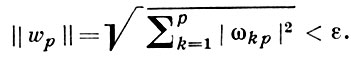
Если р = 1, то невырожденные А. ф. суть эллиптич. функции одного комплексного переменного. Каждая А. ф. с группой периодов Г естественным образом отождествляется с мероморфной функцией на комплексном торе ℂ^p /Г, т. е. на факторпространстве ℂ^p /Г (см. также Квазиабелева функция).

Исследование А. ф. началось в 19 в. в связи с проблемой обращения абелевых интегралов I рода (см. Якоби проблема обращения, [1], [2]). Возникающие при решении этой проблемы А. ф. наз. специальными А. ф., а иногда в старых работах под А. ф. только они и подразумевались. Пусть u₁, u₂, ..., u_p - линейно независимые нормальные абелевы интегралы I рода, построенные на римановой поверхности F:

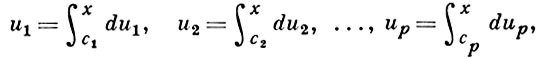
а

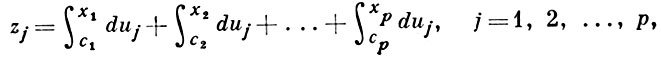
- заданная система сумм, в к-рой нижние пределы интегрирования c₁, с₂, ..., с_p считаются фиксированными на поверхности F. Тогда специальные А. ф. можно определить как все рациональные функции координат р верхних пределов x₁, x₂, ..., x_p, рассматриваемых в свою очередь как функции от р точек z₁, z₂, ..., z_p поверхности F. В символической записи, ведущей свое начало от К. Вейерштрасса (К. Weierstrass), любую специальную А. ф. Al(z) можно изобразить в виде

Al(z) = Al(z₁, z₂, ..., z_p) = R[x₁ (z₁, z₂, ..., z_p), x₂ (z₁, z₂, ..., z_p), x_p (z₁, z₂, ..., z_p)].

Соответствующие специальным А. ф. комплексные торы ℂ_p /Г являются Якоби многообразиями алгебраич. кривых.

Матрица W, столбцы к-рой образуют базис периодов А. ф. f(z), имеет размер р×2р и наз. матрицей периодов А. ф. f(z). Для того чтобы данная матрица W размера р×2р была матрицей периодов нек-рой невырожденной А. ф. f(z), необходимо и достаточно, чтобы она удовлетворяла определенным условиям (условия Римана-Фробениуса). Она должна являться римановой матрицей, т. е. для W должна существовать такая антисимметрическая неособенная целочисленная квадратная матрица М порядка 2р, что: 1) WMW^T = 0, где W^T - транспонированная матрица W; 2) матрица iWM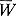^T определяет положительно определенную эрмитову форму (см. [3]). Если выразить условия 1) и 2) в виде соответственно уравнений и неравенств, то получится система р(р - 1)/2 римановых уравнений и р(р - 1)/2 римановых неравенств. Число р наз. родом матрицы W и соответствующей А. ф. f(z). Столбцы w_v = Rew_v + iImw_v матрицы W, рассматриваемые как векторы в действительном евклидовом пространстве R^2p, определяют параллелотоп периодов А. ф. f(z).

Все А. ф., соответствующие одной и той же матрице периодов W, образуют абелево функциональное поле K_W . В случае, когда поле K_W содержит невырожденную А. ф., степень его трансцендентности над полем ℂ равна р; тор ℂ^p /Г при этом является абелевым многообразием, a K_W совпадает с его полем рациональных функций. Если же все А. ф. из К_W вырожденные, то К_W изоморфно полю рациональных функций на абелевом многообразии, размерность к-рого меньше р. См. также Квазиабелева функция.

Подобно эллиптич. функциям, каждая А. ф. может быть представлена в виде отношения двух целых трансцендентных тeтa-функций, представимых в свою очередь в виде тeтa-рядов. Задание римановой матрицы W определяет класс тета-рядов, позволяющий построить все А. ф. поля К_W .

Для специальных А. ф. матрица W посредством линейного преобразования независимых переменных z₁, z₂, ..., z_p всегда может быть приведена к виду

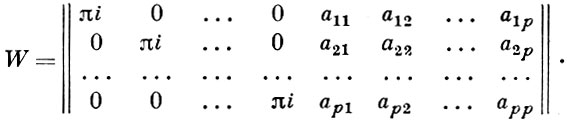
При этом римановы соотношения между элементами матрицы ||a_jk ||, j, k = 1, 2, ..., р, должны обеспечивать симметрию этой матрицы, a_jk = a_kj, и положительную определенность матрицы действительных частей ||Rea_jk ||, j, k = 1, 2, ..., р. Однако при р > 3 независимых среди элементов a_jk матрицы ||a_jk || будет только 3(р - 1), т. е. столько, сколько конформных модулей имеет риманова поверхность F, на к-рой решается проблема обращения (см. Модули римановой поверхности). Помимо римановых соотношений, в этом случае между a_jk существует (р - 2)(р - 3)/2 соотношений трансцендентной природы, явный вид которых для случая р = 4 впервые нашел в 1886 Ф. Шотки (F. Schottky; обзор последующих достижений по этой проблеме см. в [5]).

Специальные А. ф. представимы в виде отношения двух целых тета-функций с полуцелыми характеристиками специального вида. Из этого представления вытекает ряд свойств специальных А. ф., обобщающих многие свойства эллиптич. функций; так: производные А. ф. f(z) по любому аргументу z_j - суть А. ф. ; любые р + 1 А. ф. связаны алгебраич. уравнением; любую А. ф. можно выразить рационально через р + 1 нек-рых А. ф., напр. через произвольную А. ф. и ее р частных производных 1-го порядка; для А. ф. справедлива теорема сложения, т. е. значение А. ф. в точке a + b ∈ ℂ_p можно выразить рационально через значения нек-рых р + 1 А. ф. в точках а, b ∈ ℂ_p .

А. ф. имеют большое значение в алгебраич. геометрии как средство униформизации алгебраич. многообразий определенных классов.

Лит. : [1] Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960, гл. 10; [2] Чеботарев Н. Г., Теория алгебраических функций, М. - Л., 1948, гл. 8, 9; [3] 3игель К., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954; [4] Вейль А., Введение в теорию кэлеровых многообразий, пер. с франц., М., 1961; [5] Мамфорд Д., «Математика», 1973, т. 17, № 4, с. 34-49; [6] Stаhl Н., Theorie der Abelschen Funktionen, Lpz., 1896; [7] Сlebsсh A., Gоrdаn P., Theorie der Abelschen Funktionen, Lpz., 1866; Neudruck, Würzburg, 1967; [8] Conforto F., Abelsche Funktionen und algebraische Geometrie, B. - [u. a.], 1956.

E. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.