АБЕЛЕВА КАТЕГОРИЯ

Расстановка ударений: А`БЕЛЕВА КАТЕГО`РИЯ

АБЕЛЕВА КАТЕГОРИЯ - категория, обладающая рядом характерных свойств категории всех абелевых групп. А. к. были введены как основа абстрактного построения гомологич. алгебры (см. [4]). Категория наз. абелевой (см. [2]), если она удовлетворяет следующим аксиомам:

А0. Существует нулевой объект.

А1. Каждый морфизм обладает ядром и коядром.

А2. Каждый мономорфизм является нормальным мономорфизмом; каждый эпиморфизм является нормальным эпиморфизмом.

A3. Для каждой пары объектов существуют произведение и копроизведение.

Часто в определении А. к. дополнительно предполагается, что локально малая слева категория (см. Малая категория). Для А. к. это предположение равносильно локальной малости справа и, следовательно, локальной малости. Копроизведение объектов А и В А. к. наз. также прямой суммой этих объектов и обозначают А⊕ В или А + В.

Примеры А. к.

1) Категория, двойственная А. к., также является А. к.

2) Категория 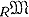всех левых унитарных модулей над произвольным ассоциативным кольцом R с единицей и всех R-модульных гомоморфизмов является А. к. (напр., категория всех абелевых групп).

3) Всякая полная подкатегория А. к., содержащая вместе с каждым морфизмом его ядро и коядро и вместе с каждой парой объектов А, В - их произведение и копроизведение, есть А. к.

Все малые А. к. исчерпываются подкатегориями указанного типа категорий 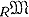левых унитарных модулей, а именно, справедлива следующая теорема Митчелла: для всякой малой А. к. существует полное точное вложение в нек-рую категорию .

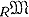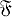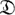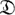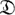4) Всякая категория диаграмм (, ) со схемой над А. к. является А. к. В схеме можно выделить множество С соотношений коммутативности, т. е. множество пар (φ, ψ) путей φ = (φ₁, ..., φ_n), φ = (ψ₁, ..., ψ_m) в 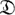с общими началом и концом. Тогда полная подкатегория категории 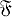(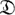, ), порожденная всеми такими диаграммами D: 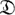→ , что

D(φ) = D(φ₁)...D(φ_n) = D(ψ₁)...D(ψ_m) = D(ψ)

является А. к. В частности, если 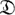- малая категория, а множество С состоит из всех пар вида (αβ, γ), где γ = αβ, то соответствующая подкатегория является А. к. одноместных ковариантных функторов из 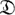в .

Пусть в малой категории 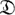есть нулевой объект; функтор F : 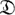→ наз. нормализованным, если он переводит нулевой объект в нулевой объект. Полная подкатегория категории функторов, порожденная нормализованными функторами, является А. к. В частности, если 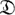- категория, объектами к-рой служат все целые числа и нулевой объект N, а ненулевые неединичные морфизмы образуют последовательность

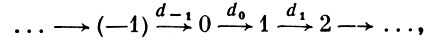
в к-рой d_n d_{n + 1} = 0, n = 0, ±1, ±2, ..., то соответствующая подкатегория, порождаемая нормализованными функторами, наз. категорией комплексов над . В категории комплексов определяются аддитивные функторы Zⁿ, Вⁿ, Нⁿ соответственно n-мерных циклов, n-мерных граней и n-мерной гомологии со значениями в и на их основе развивается аппарат гомологич. алгебры.

5) Полная подкатегория ' А. к. наз. плотной, если она содержит подобъекты и факторобъекты своих объектов и если в точной последовательности

0 → A → B → C → 0

B ∈ Ob' тогда и только тогда, когда A, C ∈ Ob'. Факторкатегория /' строится следующим образом. Пусть (R, μ] - подобъект прямой суммы А⊕ В с проекциями π₁, π₂ и пусть квадрат

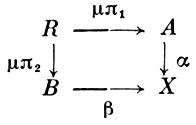
коуниверсален (т. е. является корасслоенным произведением). Подобъект (R, μ] наз. ' - подобъектом, если Coker μπ₁, Кеrβ ∈ '. Два ' - подобъекта эквивалентны, если они содержат нек-рый ' - подобъект. Множество H_/' (A, В) состоит по определению из классов эквивалентных ' - подобъектов. Обычное умножение бинарных отношений согласовано с введенной эквивалентностью, что позволяет построить факторкатегорию /', являющуюся А. к. Точный функтор Т : → /' определяется сопоставлением каждому морфизму α: А → В его графика в А⊕ В. Подкатегория наз. подкатегорией локализации, если функтор Т обладает полным унивалентным сопряжением справа функтором Q : /' → .

6) Для всякого топологич. пространства X категория левых G-модулей над X, где G-пучок колец с единицей над X, является А. к.

Во всякой А. к. можно ввести частичное суммирование морфизмов таким образом, что станет аддитивной категорией. Поэтому в А. к. произведение и копроизведение любой пары объектов совпадают. Более того, в определении А. к. можно предполагать существование либо произведений, либо копроизведений. Всякая А. к. есть бикатегория с единственной бикатегорной структурой. Перечисленные свойства характеризуют А. к. : категория с конечными произведениями является абелевой тогда и только тогда, когда она аддитивна и когда всякий морфизм α имеет ядро и коядро и разлагается в произведение

α = Coker (ker α) θ ker (Coker α),

в к-ром θ - изоморфизм.

Приведенная выше теорема Митчелла обосновывает метод «диаграммного поиска» в А. к. : всякое утверждение о коммутативных диаграммах, справедливое во всех категориях левых модулей 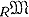и вытекающее из точности нек-рых последовательностей морфизмов, справедливо во всех А. к.

В локально малой А. к. - подобъекты любого объекта образуют дедекиндову решетку. Если в существуют произведения (или копроизведения) любого семейства объектов, то эта решетка и оказывается полной. Перечисленные условия заведомо выполняются, если в имеется образующий объект U и существуют копроизведения

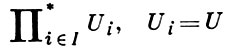
для любого множества I. Таковы, напр., Гротендика категории, эквивалентные факторкатегориям категорий модулей по подкатегориям локализации (теорема Габриеля-Попеску).

Лит. : [1] Букур И., Деляну А., Введение в теорию категорий и функторов, пер. с англ., М., 1972; [2] Freyd Р., Abelian categories, N. Y., 1964; [3] Gabriеl P., « Bull. Soc. math. France », 1962, t. 90, № 3, p. 323-448; [4] Гpотeндик А., О некоторых вопросах гомологической алгебры, пер. с франц., М., 1961.

М. Ш. Цаленко.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.