АБЕЛЕВ ИНТЕГРАЛ

Расстановка ударений: А`БЕЛЕВ ИНТЕГРА`Л

АБЕЛЕВ ИНТЕГРАЛ, алгебраический интеграл, - интеграл от алгебраической функции, т. е. интеграл вида:

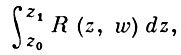
(1)

где R (z, w) - любая рациональная функция от переменных z и w, связанных алгебраич. уравнением

F(z, w) = a₀ (z)wⁿ + a₁ (z)w^n-1 + ... + a_n (z) = 0 (2)

с целыми рациональными по z коэффициентами a_j (z), j = 0, 1, ..., n. Уравнению (2) соответствует компактная риманова поверхность F, n-листно накрывающая сферу Римана, на к-рой z, w, а следовательно, и R (z, w), рассматриваемые как функции точки поверхности F, однозначны.

Интеграл (1) задается как интеграл ∫_L ω от абелева дифференциала ω = R (z, w) dz на F, взятый вдоль некоторого спрямляемого пути L. Вообще говоря, задание только начальной и конечной точек z₀ и z₁ этого пути L не вполне определяет значение А. и. (1), или, что то же, интеграл (1) является, вообще говоря, многозначной функцией от начальной и конечной точек пути L.

Поведение А. и. на F зависит прежде всего от топологич. структуры, в частности от топологич. инварианта - рода g поверхности F (см. Род поверхности). Род g связан с числом листов п и числом точек ветвления ν (взятых с надлежащей кратностью) соотношением g = ν/2 - n + 1. При g = 0 переменные z и w выражаются рационально через нек-рый параметр t, и А. и. сводится к интегралу от рациональной функции от t. Так обстоит дело, напр., в элементарных случаях w² = az + a₁ и w² = a₀ z² + a₁ z + a₂ .

При g ≥ 1 любой А. и. можно выразить в виде линейной комбинации элементарных функций и канонических А. и. трех родов. Интеграл ∫_L ω наз. А. и. I рода, если ω - абелев дифференциал I рода. Иначе, А. и. I рода характеризуется тем, что при z₀ пути L он является всюду конечной на F функцией верхнего предела z₁, вообще говоря, многозначной. Эта характеристика используется, напр., при построении аналогов А. и. I рода на некомпактных римановых поверхностях. Любой А. и. I рода может быть представлен в виде линейной комбинации g линейно независимых нормальных А. и. I рода

u₁ = ∫_L φ₁, u₂ = ∫_L φ₂, ..., u_g = ∫_L φ_g

от дифференциалов φ₁, φ₂, ..., φ_g, составляющих канонич. базис абелевых дифференциалов I рода. Если разрезать поверхность F вдоль циклов а₁ b₁ а₂ b₂ ...a_g b_g канонич. базиса гомологии, то получается односвязная область F^* . Для всех путей L^* ⊂ F^* с фиксированным началом z₀ и концом z₁ интегралы ∫_L* φ_i являются однозначными функциями верхнего предела z₁ . Многозначность интегралов u_i на F теперь полностью характеризуется тем, что интеграл u_i = ∫_L φ_i вдоль произвольного пути L ⊂ F, соединяющего те же точки z₀ и z₁, отличается от интеграла ∫_L* φ_i лишь прибавлением целочисленной линейной комбинации А-периодов A_ij и B-периодов B_ij базисных дифференциалов I рода, составляющих матрицу периодов размера g×2g, к-рая удовлетворяет билинейным соотношениям Римана (см. Абелев дифференциал).

Интеграл ∫_L ω где ω - абелев дифференциал II рода, наз. А. и. II рода. Рассматриваемый как функция от верхнего предела, он всюду на F не имеет иных особенностей, кроме полюсов. А. и. от нормированного абелева дифференциала II рода наз. нормальным А. и. II рода.

А. и. III рода - это А. и. произвольного вида. На F они допускают, вообще говоря, и логарифмич. особенности. При этом логарифмич. особенности могут встречаться только попарно. А. и. от нормального абелева дифференциала III рода наз. нормальным А. и. III рода. Любой А. и. можно представить в виде линейной комбинации нормальных А. и. I, II и III рода. В отличие от А. и. I и II рода, А. и. III рода, кроме А- и B-периодов, наз. циклическими периодами, имеет еще, вообще говоря, полярные периоды вдоль циклов, гомологичных нулю, но охватывающих логарифмич. особенности этого А. и., порождаемые полюсами абелева дифференциала ω с отличными от нуля вычетами.

Для произвольно взятых А. и. на одной и той же римановой поверхности F существуют определенные соотношения, обусловленные топологической и конформной структурой F. Напр., если ω_{Pi Pj} - нормальный абелев дифференциал III рода с простыми полюсами в точках P_i, P_j, то справедлива теорема о перестановке параметров и пределов для А. и. III рода: для любых точек Р₁, Р₂, Р₃, P₄

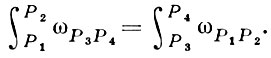
Соотношения, связывающие А. и. с рациональными функциями на F, носят назв. теоремы Абеля. Напр., в терминах дивизоров теорема Абеля для А. и. I рода имеет вид: дивизор 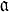на F является дивизором мероморфной функции тогда и только тогда, когда существует такая цепь L, что ∂L = 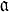и ∫_L ω = 0 Для всех абелевых дифференциалов I рода на F. Существуют варианты теоремы Абеля для А. и. II и III рода (см. [4]). А. и., и в частности теорема Абеля, служат основой для трансцендентного построения Якоби многообразия римановой поверхности. Вопрос обращения А. и. как функции верхнего предела ведет также к понятиям абелевых функций, эллиптических функций и тета-функций (см. Якоби проблема обращения).

Исторически начало теории А. и. было положено рассмотрением поверхности рода g = l. Записав соответствующее уравнение в виде:

F(z, w) = w² - f(z) = 0,

где f(z) - многочлен от z 3-й или 4-й степени, получают в качестве соответствующих А. и. эллиптические интегралы. Впервые они появились при спрямлении дуг кривых 2-го порядка в работах Я. и И. Бернулли (Jacob Bernoulli, Johann Bernoulli), Дж. Фаньяно (G. Faniano) конца 17 и начала 18 вв. Л. Эйлер (L. Euler) подошел к теореме сложения для эллиптич. интегралов - частному случаю теоремы Абеля (1752). В 1827 в работах Н. Абеля (N. Abel) и К. Якоби (С. Jacobi) была поставлена и решена проблема обращения эллиптич. интегралов. Тем самым было положено начало теории эллиптич. функций. Однако нек-рыми фактами этой теории владел уже к началу 18 в. К. Гаусс (С. Gauss). Проблема обращения А. и. в гораздо более сложном случае g > l возникла в работах Н. Абеля и К. Якоби. В самом начале развития теории большое внимание привлек случай гиперэллиптических интегралов, когда F (z, w) = w² - f(z), где f(z) - многочлен 5-й или 6-й степени без кратных корней. Здесь g = 2 и трудности проблемы обращения уже достаточно ощутимы. Существенное продвижение в теории А. и. связано с именем Б. Римана (В. Biemann), к-рый ввел понятие римановой поверхности (1851), сформулировал и доказал ряд важных результатов.

Многомерные обобщения теории А. и. изучаются в алгебраич. геометрии и теории комплексных многообразий.

Лит. : [1] Чеботарев Н. Г., Теория алгебраических функций, М. - Л., 1948, гл. 8, 9; [2] Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960, гл. 10; [3] Неванлинна Р., Униформизация, пер. с нем., М., 1955, гл. 5; [4] Вliss G. A., Algebraic functions, N. Y., 1966; [5] Stahl H., Theorie der Abelschen Funktionen, Lpz., 1896; [6] Шафapeвич И. P., Основы алгебраической геометрии, М., 1972.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.