
АБЕЛЕВ ДИФФЕРЕНЦИАЛ
Расстановка ударений: А`БЕЛЕВ ДИФФЕРЕНЦИА`Л
АБЕЛЕВ ДИФФЕРЕНЦИАЛ - голоморфный или мероморфный дифференциал на компактной, или замкнутой, римановой поверхности S (см. Дифференциал на римановой поверхности).
Пусть g - род поверхности S; a1 b1 a2 b2 ... ag bg - циклы канонич. базиса гомологии S. В зависимости от характера особенностей различают А. д. трех родов: I, II и III, причем имеют место строгие включения: I ⊂ II ⊂ III. А. д. I рода - это голоморфные всюду на S дифференциалы 1-го порядка, к-рые в окрестности U каждой точки P0 ∈ S имеют вид (ω = pdz = p(z)dz, где z = x + iy - локальная униформизирующая переменная в U, dz = dx + idy, а р(z) - голоморфная, или регулярная, аналитич. функция от z в U. Сложение А. д. и умножение на голоморфную функцию определяются естественными правилами: если
ω = pdz, π = qdz, a = a(z),
то
ω + π = (p + q)dz, aω = (ap)dz.
А. д. I рода образуют векторное пространство 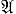 размерности g. После введения скалярного произведения
размерности g. После введения скалярного произведения
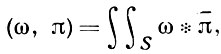
где ω *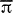 - внешнее произведение со на звездно сопряженный дифференциал
- внешнее произведение со на звездно сопряженный дифференциал 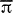 , пространство
, пространство 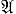 превращается в гильбертово пространство.
превращается в гильбертово пространство.
Пусть А1, В1, А2, В2, ..., Ag, Bg суть А- и В-периоды А. д. I рода ω, т. е. интегралы
Aj = ∫aj ω, Bj = ∫bj ω, j = 1, 2, ..., g.
Тогда имеет место соотношение:
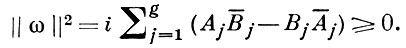
(1)
Если А1', В1', А2', В2', ..., Ag', Bg' - периоды другого А. д. I рода π, то
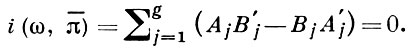
(2)
Соотношения (1) и (2) наз. билинейными соотношениями Римана для А. д. I рода. Канонич. базис А. д. I рода, т. е. канонич. базис φ1, φ2, ..., φg пространства 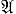 , выбирается таким образом, что
, выбирается таким образом, что
Aij = ∫ai φi = δij,
где δii = 1 и δij = 0 при i ≠ j. При этом матрица (Вij), i, j = 1, 2, ..., g, B-периодов
Bij = ∫bj φi
симметрическая, а матрица мнимых частей (Im Вij) положительно определенная. А. д. I рода, у к-рого все A-периоды или все B-периоды равны нулю, тождественно равен нулю. Если все периоды А. д. I рода ω действительны, то ω = 0.
А. д. II и III рода относятся, вообще говоря, к мероморфным дифференциалам, т. е. к таким аналитич. дифференциалам, к-рые имеют на S не более чем конечное множество особенностей типа полюсов с локальным представлением
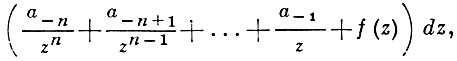
(3)
где f(z) - регулярная функция, n - порядок полюса (если а-n ≠ 0), а-1 - вычет в данном полюсе. При n = 1 полюс наз. простым. А. д. II рода - это мероморфные дифференциалы, у к-рых все вычеты равны нулю, т. е. мероморфные дифференциалы с локальным представлением
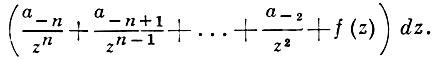
А. д. III рода - это А. д. произвольного вида.
Если ω - произвольный А. д. с А-периодами А1, А2, ..., Ag, то А. д. ω' = ω - А1 φ1 - А2 φ2 -... - Ag φg имеет нулевые A-периоды и наз. нормированным А. д. В частности, если Р1 и Р2 - любые различные точки S, то можно построить нормированный А. д. ω1, 2 с особенностями (1/z)dz в Р1 и (- 1/z)dz в Р2, к-рый наз. нормальным А. д. III рода. Пусть ω - произвольный А. д. с вычетами с1, с2, ..., сn в точках Р1, Р2, ..., Рn соответственно, при этом всегда с1 + с2 + ... + сn = 0. Если Р0 - произвольная точка на S такая, что Р0 ≠ Рj, j = 1, 2, ..., n, то ω можно представить в виде линейной комбинации нормированного А. д. II рода ω2, конечного числа нормальных А. д. III рода ωi, 0 и базисных А. д. I рода φk :
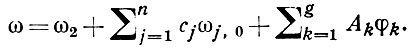
Пусть ω3 - А. д. III рода, имеющий только простые полюсы с вычетами сj в точках Pj, j j = 1, 2, ..., n, a ω1 - произвольный А. д. I рода;
Ak = ∫ak ω1, Bk = ∫bk ω1,
причем циклы ak, bk не проходят через полюсы ω3 . Пусть точка P0 ∈ S не лежит на циклах аk, bk и Lj есть путь от Р0 к Pj . Тогда имеем билинейные соотношения для А. д. I и III рода:
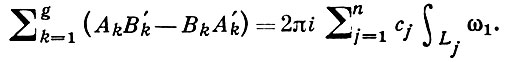
Между А. д. I и II рода также имеются билинейные соотношения аналогичного вида.
Произвольный А. д. III рода, кроме А- и B-периодов Ak, Bk, k = = l, 2, ..., g, наз. циклическими периодами, имеет еще полярные периоды вида 2 π icj вдоль циклов, гомологичных нулю, но охватывающих полюсы Pj . Таким образом, для произвольного цикла у имеем:
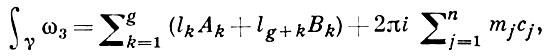
где lk, lg + k, mj - целые числа.
Важные свойства А. д. описываются в терминах дивизоров. Пусть (ω) - дивизор А. д. ω, т. е. выражение вида (ω) = Р1α 1 Р2α 2 ...Р3α 3, где Pj - все нули и полюсы ω, а αj - их кратности, или порядки. Степень дивизора d[(ω)] = α1 + α2 + ... + αn для А. д. ω зависит только от рода S, а именно всегда d[(ω)] = 2g - 2. Пусть 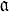 - нек-рый произвольно заданный дивизор. Обозначим через Ω (
- нек-рый произвольно заданный дивизор. Обозначим через Ω (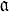 ) комплексное векторное пространство А. д. ω, дивизоры к-рых (ω) кратны
) комплексное векторное пространство А. д. ω, дивизоры к-рых (ω) кратны 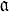 ; L (
; L (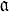 ) - векторное пространство мероморфных функций f на S, дивизоры к-рых (f) кратны
) - векторное пространство мероморфных функций f на S, дивизоры к-рых (f) кратны 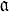 . Тогда размерность dim Ω (
. Тогда размерность dim Ω (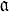 ) = dim L (
) = dim L (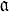 /(ω)). Другая важная информация о размерности этих пространств содержится в теореме Римана-Роха: для любого дивизора
/(ω)). Другая важная информация о размерности этих пространств содержится в теореме Римана-Роха: для любого дивизора 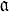 имеем равенство:
имеем равенство:
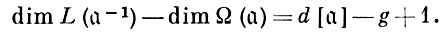
Отсюда следует, напр., что при g = 1, т. е. на поверхности тора, мероморфная функция не может иметь единственный простой полюс.
Пусть S - произвольная компактная риманова поверхность, на к-рой z и w - мероморфные функции, удовлетворяющие неприводимому алгебраич. уравнению F(z, w) = 0. Произвольный А. д. ω на S можно выразить тогда в виде ω = R(z, w)dz, где R (z, w) - нек-рая рациональная функция от z и w, и обратно: выражение ω = R(z, w)dz есть А. д. Таким образом, произвольный абелев интеграл
∫ R (z, w) dz = ∫ ω
является интегралом от нек-рого А. д. на компактной римановой поверхности S.
См. также Алгебраическая функция.
Лит. : [1]Спрингер Дж., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [2] Неванлинна Р., Униформизация, пер. с нем., М., 1955; [3] Чеботарев Н. Г., Теория алгебраических функций, М. - Л., 1948.
Е. Д. Соломенцев.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'