Интуитивный математик

На правом берегу Сены, поблизости от дворца Альма вознеслось квадратное, тяжелое здание с широкими окнами, отделанными массивными украшениями. Крышей ему служит просторная терраса, на которой укреплены позолоченные мачты с развевающимися на них флагами. Это Дворец конгрессов при Всемирной парижской выставке 1900 года, самой грандиозной и великолепной из всех всемирных выставок. Здесь обычно происходят торжественные открытия многочисленных (свыше ста) международных конгрессов по самым различным вопросам, которые собираются в Париже с начала лета поочередно и по нескольку одновременно. Уже на следующий день после окончания работы философского конгресса состоялось открытие математического конгресса.

На фоне проходившего в это же время многолюдного и шумного конгресса студентов всеобщий съезд математиков выглядел весьма скромно и не привлек внимания широкой прессы. Это был уже второй Международный математический конгресс. Первый состоялся еще в 1897 году в Цюрихе (Швейцария) и собрал около 240 участников из 16 стран. Пуанкаре выступил на нем с докладом "О соотношении между чистым анализом и математической физикой", который произвел тогда большое впечатление. Конгресс показался многим настолько удачным, что участники его поручили Французскому математическому обществу организовать через некоторое время второй конгресс математиков в Париже. Организационный комитет возглавили два авторитетнейших представителя французских математических кругов: Г. Дарбу и А. Пуанкаре. Второму Международному математическому конгрессу предстояло на деле показать, возможны ли периодические съезды математиков разных стран или же цюрихский эксперимент оказался лишь счастливым исключением и в математическом мире действуют неодолимые центробежные силы.

Далеко не все верили в успех этого предприятия, в солидарность разделенных государственными границами математиков, "по характеру своей науки, казалось бы, наиболее подготовленных к международной организации, но на практике оказывающихся зачастую крайними националистами", как писал в то время русский математик Д. Синцов. Особенно сомнительным представлялось прибытие в Париж сколько-нибудь представительной делегации немецких математиков.

В конце XIX века на первом месте по числу активно работающих ученых, по количеству печатных изданий, по организованности и по значению в культурной и общественной жизни своих стран стояли математики Франции и Германии. На подъеме была итальянская математика. В России в самом расцвете была "могучая кучка" математиков чебышевской школы. В Англии после смерти Сильвестра и Кэли репутация математических наук уже не была столь высокой, и математические исследования стимулировались в основном решением тех или иных теоретических проблем механики. Поэтому отсутствие немецких математиков, несомненно, сказалось бы па работе конгресса и на его международном престиже. Но, к счастью, опасения эти не оправдались. Около 250 ученых из многих стран Европы, из Северной и Южной Америки и из Японии съехались в Париж на этот конгресс. Из Германии прибыли 25 человек, в числе которых были такие ведущие математики, как Ф. Клейн, Г. Кантор, Д. Гильберт. "...Казавшийся почти невозможным съезд в Париже при участии немецких математиков состоялся. Минуты, проведенные вместе за общим мирным делом, не пройдут без следа, и, как другие международные съезды, математический съезд внес свое в дело устранения вражды между народами",- отмечает участник конгресса Д. Синцов. Немногочисленной оказалась лишь английская делегация, что опять-таки объяснялось чисто политическими причинами: симпатией французов к бурам, ведущим войну с Англией.

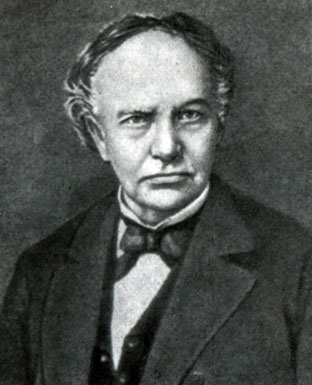
Шарль Эрмит

Торжественное открытие конгресса состоялось 6 августа во Дворце конгрессов. Председателем был избран Анри Пуанкаре, почетным председателем - отсутствовавший (видимо, по болезни) Шарль Эрмит. В числе вице-председателей были Г. Миттаг-Леффлер и В. Вольтерра, известный математик из Турина. На следующий день участники конгресса покинули территорию выставки и перебрались в Латинский квартал, где в здании Сорбонны проходила работа всех шести секций. На секционных заседаниях наиболее интересным оказался доклад геттингенского профессора Д. Гильберта, уже хорошо известного своими работами по теории инвариантов и теории алгебраических чисел. Его знаменитые "Основания геометрии", вышедшие в свет за год до этого, заслужили высокую, оценку Пуанкаре и многих других его коллег. Этот тридцативосьмилетний математик с трибуны конгресса дал весьма необычный прогноз развития математики в грядущем столетии: он перечислил проблемы, на которых будут сконцентрированы творческие усилия ученых в последующие десятилетия^*. Гильберт подчеркивает важность проблем для формирования направлений развития любой науки. Все перечисленные им проблемы действительно явились вехами в развитии математики XX века.

^* (22-я проблема Гильберта формулируется следующим образом: "Обобщить теорему Пуанкаре, утверждающую, что любое алгебраическое соотношение между двумя переменными можно упиформизовать с помощью автоморфных функций от одной переменной". Проблема эта была решена в 1907 году самим Пуанкаре и одновременно Кебе.)

На последнем общем заседании, состоявшемся в субботу 11 августа, выступили только Миттаг-Леффлер, рассказавший о последних годах жизни Вейерштрасса, и Пуанкаре. "О роли интуиции и логики в математике" - такова тема его выступления. Председатель конгресса избрал одну из наиболее дискутируемых в то время общих проблем математики. Деление представителей этой науки на интуитивистов и логиков уже не было новостью. Такой классификации придерживался, например, Ф. Клейн. Пуанкаре по-разному подходит к различению математиков по их творческой манере. В качестве различительного признака он рассматривал, например, обобщающую способность их творчества. "Некоторые среди них любят лишь общие суждения, при наличии результата они стремятся мгновенно его обобщить, стараются сопоставить с ним близкие результаты, как бы делая из них фундамент наиболее высокой пирамиды, откуда они будут видеть дальше,- писал он как-то.- Есть и другие, которые являются противниками этих слишком широких взглядов, поскольку, как бы ни был красив обширный пейзаж, удаленные горизонты всегда несколько неопределенны. Они предпочитают ограничиться, чтобы лучше видеть подробности и приводить их к совершенству; они работают, как чеканщик; они больше художники, чем поэты". Нечего и говорить, что сам Пуанкаре принадлежал к математикам первого типа.

Но сейчас он обращает внимание на несходство математиков-логиков и математиков-интуитивистов. Об этом Пуанкаре писал еще год назад в одной из своих статей, к этому же вопросу он вернется несколько лет спустя в своей книге "Ценность науки": "Одни прежде всего заняты логикой; читая их работы, думаешь, что они продвигались вперед шаг за шагом с методичностью Вобана, который готовит штурм крепости, ничего не оставляя на волю случая. Другие руководствуются интуицией и с первого удара добиваются побед, но иногда ненадежных, так же как отчаянные кавалеристы авангарда". Спорным остается вопрос о соотношении логического и интуитивного в математическом творчестве. Вскоре этот спор перерастет в ожесточенную полемику по обоснованию математики вообще, в которую будут втянуты некоторые ведущие ученые разных стран, в том числе Пуанкаре. Пока же его интересует лишь доля участия логики и интуиции в творческом процессе. Немало сторонников и у того и у другого метода. "Любое человеческое знание начинается с интуиции, затем переходит к понятиям и завершается идеями",- писал в свое время Кант. Великий Гаусс, целиком полагавшийся в своих математических доказательствах на собственную интуицию, признавался: "Мои результаты мне давно известны; я только не знаю, как я к ним приду". По мнению Клейна, исследователь в математике "существенно пользуется своей фантазией и продвигается вперед индуктивно, опираясь на эвристические вспомогательные средства". Сам Клейн послужил для Пуанкаре примером творца, для которого весьма значительную роль играют непосредственные, наглядные представления. Докладчик вспоминает о том, как немецкий математик при доказательстве теорем из теории абелевых интегралов плодотворно использовал картины течения жидкости. Приводит он и другие, прямо противоположные примеры. Математику одинаково необходимы и интуиция и логика, считает Пуанкаре. Преобладание же той или другой обусловлено лишь его индивидуальными особенностями. Но функции этих двух методов, безусловно, различны. Об этом он хорошо напишет позднее в книге "Наука и метод": "Логика говорит нам, что на таком-то и таком-то пути мы, наверное, не встретим препятствий; но она не говорит, каков путь, который ведет к цели. Для этого надо издали видеть цель, а способность, научающая нас видеть, есть интуиция. Без нее геометр был бы похож на того писателя, который безупречен в правописании, но у которого нет мыслей".

По мнению Пуанкаре, разум - слуга двух господ: логика доказывает, а интуиция творит. И та и другая равно необходимы в математических исследованиях. И все же чаша весов заметно склоняется у него в пользу интуиции. Нужно ли этому удивляться! Ведь сколько раз именно интуиция приводила Пуанкаре к новым результатам, позволяла увидеть скрытые возможности. Интуитивный характер его творчества подтверждался многими из его современников. "Он ожидал, что истина разразится над ним, подобно грому",- вспоминает о нем Пьер Бутру. "Его мысль рождалась, так сказать, вне его",- вторит ему Жак Адамар. А. Ф. Массой в своем приветственном докладе по поводу вступления Пуанкаре во Французскую академию скажет: "В отдыхе ваш мозг продолжает механически свою работу, даже когда вы не осознаете этого; плод формируется, растет, зреет, отрывается, и вы выражаете нам свое удивление, весьма кстати находя его под рукой".