
Глава 46. Полиомино и "прочные" прямоугольники
В главе 12 уже говорилось о полиомино и его создателе С. Голомбе. После опубликования статьи о полиомино на страницах журнала Scientific American (1957) игра стала необыкновенно популярным математическим развлечением. Обнаружились сотни новых задач и причудливых конфигураций полиомино. О них и пойдет здесь речь.
Напомним, что пентамино называют фигуры, которыми на шахматной доске можно покрыть пять соседних клеток, образующих связную область. Существует двенадцать таких фигур. Если эти фигуры расположить так, как показано на рис. 236, то становится видно, что каждая фигура по форме напоминает какую-нибудь латинскую букву, поэтому для запоминания формы и названия фигур (каждую фигуру мы будем называть какой-нибудь буквой) достаточно знать конец латинского алфавита (Т, U, V, W, X, Y, Z) и слово FiLiPiNo.
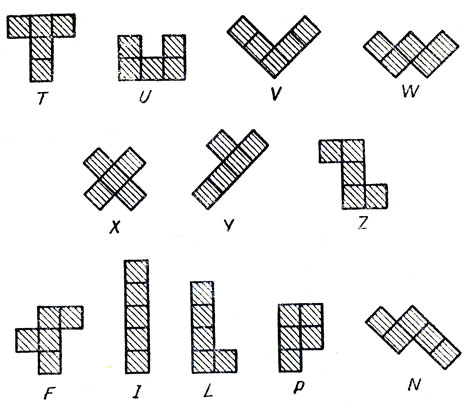
Рис. 236
В главе 12 (рис. 71) было показано, что из двенадцати элементов пентамино общей площадью в 60 квадратиков можно сложить прямоугольники четырех размеров: 3×20, 4×15, 5×12 и 6×10. Те же 12 фигур можно уложить на шахматной доске размером 8×8, причем квадрат из четырех лишних клеток (площадь доски равна 64 квадратикам) может находиться в любом месте доски. Любой элемент пентамино можно утроить с помощью каких-нибудь девяти фигур из числа оставшихся (подразумевается, что из этих девяти пентамино будет сложена фигура, подобная выбранной, но в три раза выше и длиннее). Из двенадцати пентамино можно еще построить два прямоугольника 5×6. Последняя задача носит название задачи на суперпозицию, потому что построенные фигуры можно наложить друг на друга. Голомб сообщил мне пять новых задач на суперпозицию, которые впервые публикуются в этой книге. Если читатель до сих пор не понял всей прелести пентамино, ему необходимо вырезать из картона набор элементов пентамино и поломать голову над некоторыми из приведенных ниже задач. Во всех головоломках элементы пентамино можно класть на плоскость любой стороной.
- Разбейте двенадцать пентамино на три группы по четыре элемента в каждой. Затем найдите фигуру площадью в 20 квадратиков, которую можно сложить из элементов каждой группы. Одно из возможных решений изображено на рис. 237.
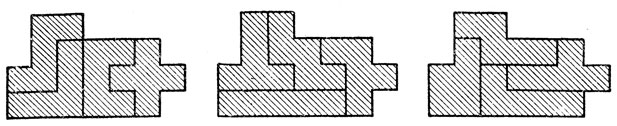
Рис. 237 - Разбейте двенадцать пентамино на три группы но четыре элемента. Каждую группу разделите пополам и найдите такую фигуру (для каждой группы свою), имеющую площадь в 10 квадратиков, которую можно сложить из обеих пар элементов в отдельности. Одно из решений показано на рис. 238. Можете ли вы придумать другие решения, чтобы хотя бы в одном из них фигуры не имели отверстий?
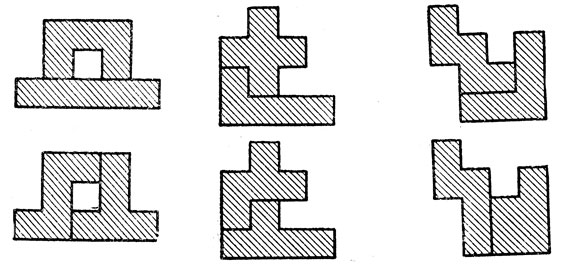
Рис. 238 - Разбейте двенадцать пентамино на три группы по четыре элемента в каждой. К каждой группе добавьте мономино (один квадратик) и постройте прямоугольник размером 3×7. Как это сделать, показано на рис. 239. Решение единственно с одной лишь оговоркой: в первом прямоугольнике мономино и элемент Y пентамино можно переворачивать, не меняя общей формы и площади составленной из них односвязной фигуры.
Доказать единственность решения можно следующим образом. Прежде всего заметим, что на рис. 240 элемент X должен обязательно использоваться в паре с элементом U. Ни элемент F, ни элемент W не годятся для того, чтобы завершить построение прямоугольника. Если элемент X дополнить элементом U, то в том же самом прямоугольнике 3×7 уже нельзя будет использовать элементы F и W. Следовательно, из трех прямоугольников размером 3×7 в одном будут использованы элементы X и U, второй будет содержать элемент W (но не U), а третий - элемент F (но не U). Если теперь перебрать все возможные варианты прямоугольников и сравнить их (это отнимет у вас достаточно много времени), то окажется, что предполагаемое решение (см. рис. 239) единственно.

Рис. 239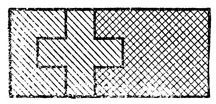
Рис. 240 - Разбейте двенадцать пентамино на четыре группы по три элемента в каждой. Найдите такой многоугольник площадью в 15 квадратов, который можно сложить из трех элементов каждой группы. Решение этой головоломки неизвестно; с другой стороны, никто до сих пор не доказал, что задача неразрешима.
- Найдите на шахматной доске область минимального размера, на которой умещается любой из двенадцати элементов пентамино. Минимальная площадь такой области равна девяти квадратам, и известно всего две ее формы (рис. 241).
Каждая фигура рис. 241 удовлетворяет поставленным условиям; для доказательства достаточно заметить, что на ней умещается любой элемент пентамино. Доказательство того, что число квадратов не может быть меньше девяти, проводится следующим образом. Если бы годилась фигура, содержащая меньше девяти квадратов, то элементами I, X и V можно было бы закрыть не более восьми квадратов. При этом у элементов I и X было бы три общих квадрата. (В противном случае либо потребовалось бы девять квадратов, либо, что было бы излишней роскошью, самая длинная прямая состояла бы из шести квадратов.) Этого можно достичь всего лишь двумя разными способами (рис. 242), но в том и в другом случае нужен еще и девятый квадрат, чтобы уместить элемент U. Таким образом, восьми квадратов не хватает, в то время как из приведенных примеров видно, что девяти квадратов достаточно.
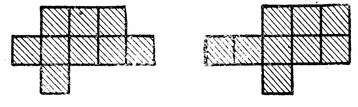
Рис. 241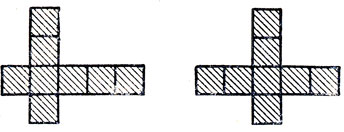
Рис. 242
В последнее время задачи о пентамино начали исследовать на электронно-вычислительных машинах. В главе 12 уже упоминалось о том, как Дана Скотт с помощью электронно-вычислительной машины нашла все способы составления из двенадцати элементов пентамино шахматной доски размером 8×8 с квадратным отверстием в четыре клетки в центре. Было найдено 65 принципиально различных решений (два решения, получающиеся одно из другого поворотом или отражением, считаются одинаковыми). Не так давно К. Б. Хейселгроув, математик из Манчестерского университета, перечислил с помощью машины все возможные варианты прямоугольника размером 6×10, сложенного из двенадцати пентамино. Он нашел 2389 различных решений, не считая тех, которые получаются друг из друга поворотами и отражениями! Кроме того, он проверил программу, составленную Дамой Скотт для шахматной доски 8×8.
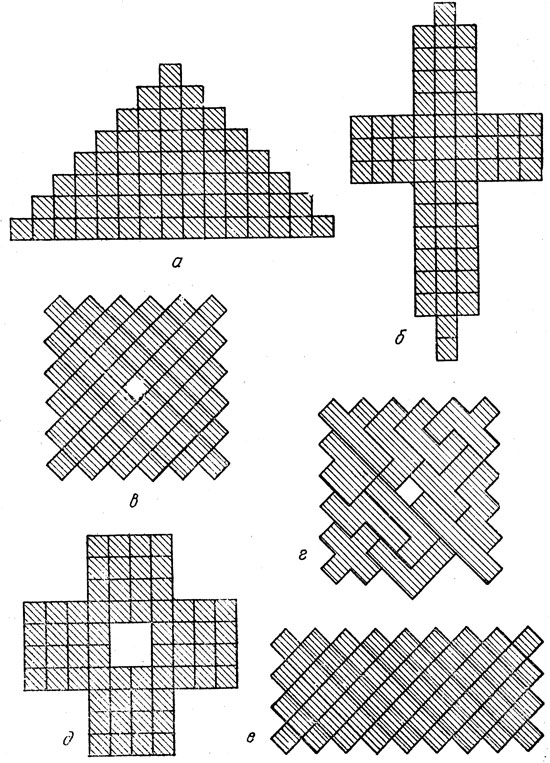
Рис. 243
Из пентамино получаются прекрасные головоломки. На рис. 243, а изображена пирамида из 64 клеток, которую можно сложить из двенадцати элементов пентамино и квадратного тетрамино 2×2. Необыкновенно сложно собрать из двенадцати пентамино крест, показанный на рис. 243, б. Для фигуры, изображенной на рис. 243, в, решения до сих пор не найдено (никто ее не сложил, но и невозможность построения тоже не доказана). Даже для случая, когда отверстие в форме мономино вырезано в другом месте, решения тоже не найдено. Рис. 243, г представляет собой фигуру, наиболее близкую по форме к предыдущей. По-видимому, также неразрешима головоломка Герберта Тейлора, показанная на рис. 243, д; правда, до сих пор никому не удалось доказать, что решения не существует.
К счастью, не все нерешенные задачи окутаны мраком неизвестности. Так, Т. М. Робинсон доказал, что, например, фигуру, которая изображена на рис. 243, е, нельзя сложить из двенадцати пентамино. С краев она ограничена 22 квадратами, а если внимательно изучить элементы пентамино и выписать, сколько квадратов каждого элемента может находиться на краю складываемой фигуры, то в сумме для всех элементов это число окажется равным 21, то есть на единицу меньше, чем надо. Такой способ рассуждений обычно используется в головоломках о складывании зигзагообразных брусочков. (На бумаге или картоне надо нарисовать прямоугольник с пилообразным краем и разрезать его на куски любой формы. Перемешайте куски и попробуйте сложить из них первоначальный прямоугольник.) Обычно различают внутренние и внешние части фигуры и в первую очередь стараются сложить края головоломки.
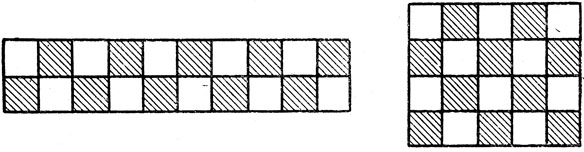
Рис. 244
Полиомино, занимающие четыре квадрата шахматной доски, называются тетрамино. В отличие от пентамино из пяти его различных элементов нельзя сложить прямоугольник. Для доказательства раскрасим в шахматном порядке прямоугольники площадью в 20 квадратов - их всего два: 4×5 и 2×10 (рис. 244). Четырьмя из пяти элементов тетрамино можно накрыть два черных и два белых квадрата (рис. 245), а пятый, Т-образный элемент, всегда покрывает три квадрата одного цвета и один - другого. Поэтому все пять фигур тетрамино вместе занимают область, состоящую из нечетного числа квадратов каждого цвета, а оба прямоугольника, о которых идет речь, содержат по 10 квадратов каждого цвета, то есть состоят из четного числа квадратов.

Рис. 245
С другой стороны, если взять несколько разных элементов пентамино, то любой из них вместе с пятью тетрамино образует набор, из которого можно построить квадрат размером 5×5. Два примера таких построений показаны на рис. 246. Возникает интересный вопрос: сколько разных пентамино можно использовать для этой цели?
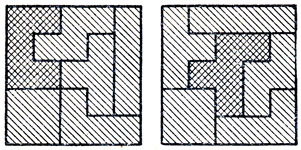
Рис. 246
Аспирант-математик Орегонского университета Р. Джуэтт предложил задачу о домино (полиомино из двух квадратов), совершенно непохожую на те задачи, которыми мы занимались до сих пор. Существует ли такой прямоугольник, сложенный из костей домино, в котором нельзя провести ни вертикальную, ни горизонтальную прямую, соединяющую противоположные стороны? В прямоугольнике, изображенном на рис. 247, для примера такая линия проведена между верхним и нижним основаниями. Если представить себе, что - вместо домино взяты кирпичи, то существование такой линии ("шва") будет свидетельствовать о непрочной кладке. Таким образом, Задача Джуэтта сводится к вопросу о том, как надо класть прямоугольные кирпичи, чтобы постройка не развалилась. Соответствующие прямоугольники мы в дальнейшем будем называть "прочными" прямоугольниками. Очень многие, взявшись за эту задачу, вскоре сдаются, уверенные, что она неразрешима; на самом же деле существует бесконечное множество ее решений.
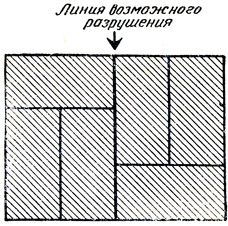
Рис. 247
Я предлагаю читателю вооружиться набором домино (более чем достаточно взять обычный комплект из 28 костей) и попытаться определить размеры самого маленького из "прочных" прямоугольников, который можно из них сложить.
* * *
С тех пор как эта глава появилась в Scientific American, в изучении полиомино и "прочных" прямоугольников произошли большие изменения. В 1965 году вышла книга Голомба "Полиомино", в которой проводится тщательное исследование предмета*.
* (S. W. Golomb, Polyominocs, New York, Scribner, 1965.)
Выяснилось, что головоломка Г. Тейлора (рис. 243, д) и зубчатый квадрат (рис. 243, в) неразрешимы; однако ни для той, ни для другой фигуры до сих пор не найдено краткого и изящного доказательства невозможности их построения.
Можно сложить зубчатый квадрат, в котором мономино (отверстие) находится на краю, рядом с углом или в углу. Найдены шестнадцать разных решений последнего типа. Однако пока не известно, может ли мономино отстоять от угла дальше чем на одну клетку.
Пэттон, много лет занимающийся "прочными" прямоугольниками, составленными из домино, прислал мне новые интересные задачи. Каковы, например, минимальные размеры "прочного" прямоугольника, в котором одинаковое число костей домино расположено по вертикали и горизонтали? Может быть, читателю захочется самому найти решение, поэтому я привожу только ответ: размер прямоугольника 5×8.
Складывая из домино "прочные" квадраты, можно придумать массу игр, которые, насколько мне известно, совсем не изучены. Например, противники кладут по очереди домино на квадратную шахматную доску. Выигрывает тот, кто первым построит вертикальную и горизонтальную линии "потери прочности" или наоборот: тот, кто первым построит такие линии, проигрывает.
Ответы
На рис. 248 и 249 показано, как можно сложить пирамиду и крест. Оба решения не являются единственными.
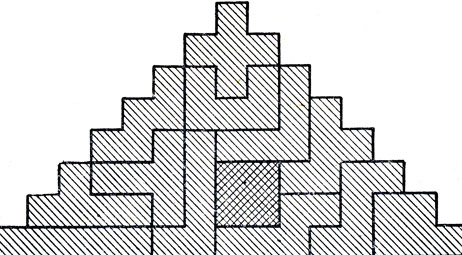
Рис. 248. Как сложить пирамиду
Для определения того, какой элемент пентамино надо добавить к пяти тетрамино, чтобы из всех шести фигур можно было построить квадрат размером 5×5, годятся все элементы пентамино, кроме элементов I, T, X и V.
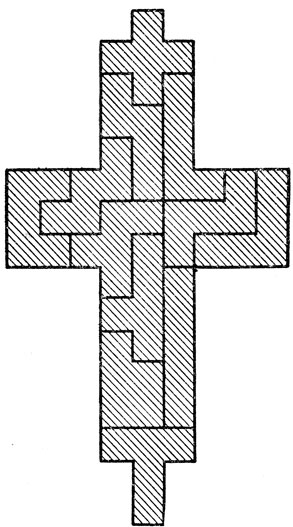
Рис. 249. Как выложить крест
Самый маленький "прочный" прямоугольник, который можно сложить из домино, имеет размер 5×6. Два принципиально различных решения изображены на рис. 250.
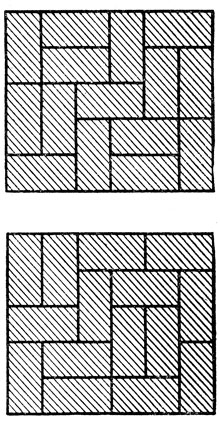
Рис. 250. Ответы к задачам о 'прочных' прямоугольниках
Нетрудно показать, что минимальная ширина "прочного" прямоугольника должна быть больше четырех. (Случаи, когда ширина прямоугольника равна 2, 3 и 4, лучше всего рассматривать по отдельности.) Поскольку квадрат размером 5×5 состоит из нечетного числа квадратов, а площадь области, построенной из домино, всегда четна, то минимальные размеры прямоугольника равны 5×6.
Прямоугольник 5×6 можно увеличить до размеров шахматной доски (8×8), и он все-таки будет "прочным". Пример такого построения изображен на рис.251. Как это ни удивительно, но не существует "прочных" прямоугольников размером 6×6. Этот факт имеет замечательное доказательство.
Представьте себе, что прямоугольник 6×6 целиком покрыт домино. Для этого нужно 18 костей домино (половина площади), а чтобы разделить прямоугольник на клетки, понадобится 10 линий (пять вертикальных и пять горизонтальных). Прямоугольник будет "прочным", если прямая из образующих сетку пересекает по крайней мере одно домино.

Рис. 251. Прочный прямоугольник на шахматной доске размером 8×8 клеток
Приступая к доказательству, прежде всего покажем, что в любом "прочном" прямоугольнике каждая прямая сетки границ пересекает четное число элементов домино. Рассмотрим любую вертикальную прямую сетки. Площадь слева от нее четна (то есть выражается четным числом единичных квадратов): 6, 12, 18, 24 или 30. Те домино, которые целиком находятся слева от этой прямой, должны занимать четную площадь, поскольку каждый элемент домино покрывает два квадрата. Домино, которые разрезаются этой прямой, тоже занимают слева от нее четную площадь, потому что эта площадь равна разности двух четных чисел (всей площади слева от прямой и площади неразрезанных домино, тоже находящихся слева). Но поскольку разрезанное домино занимает всего один квадрат слева от выбранной прямой, то число элементов домино, разрезаемых прямой, должно быть четным. Сетка в квадрате 6×6 состоит из десяти прямых. Чтобы прямоугольник был "прочным", каждая прямая должна пересекать по крайней мере два домино. Ни одно домино нельзя пересечь более чем одной линией сетки, поэтому сетка разрезает по крайней мере двадцать домино. А в квадрате 6×6 всего лишь восемнадцать домино!
Аналогичным образом можно показать, что прямоугольник 6×8 будет "прочным" только в том случае, если каждый отрезок сетки границ пересекает ровно два домино. Такой прямоугольник изображен на рис. 252.
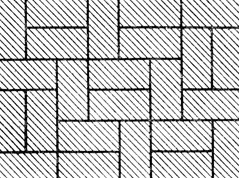
Рис. 252. Прочный прямоугольник 6×8
В самом общем виде результат можно сформулировать так: из домино можно сложить "прочный" прямоугольник, если его площадь четна, а длина и ширина больше четырех; исключение составляет квадрат 6×6. В действительности, чтобы сложить прямоугольник большего размера, нужно применить к прямоугольникам 5×6 и 6×8 метод увеличения длины или ширины на две единицы. Проще всего объяснить, как это делается, с помощью рис. 253. Для удлинения фигуры в горизонтальном направлении на две единицы надо положить по одному домино рядом с каждым домино, лежащим горизонтально, а все вертикальные домино надо выдвинуть до новых границ, заложив освободившееся место горизонтальными домино.
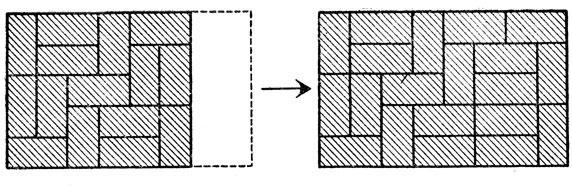
Рис. 253. Общее решение задачи о построении прочного прямоугольника
Может быть, для читателя окажется интересным рассмотреть в качестве кирпичей элементы тримино. В частности, возникает вопрос: каковы наименьшие размеры "прочного" прямоугольника, который можно сложить из двух или большего числа "прямых тримино" (то есть прямоугольников размером 1×3)?
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'