Глава 43. Проблема четырех красок

Из всех великих математических гипотез, не доказанных и не опровергнутых по сей день, простейшей - в том смысле, что понять ее может даже маленький ребенок,- следует считать знаменитую топологическую проблему четырех красок, Предположим, что нам требуется раскрасить географическую карту. Сколько красок нужно взять для того, чтобы никакие две "сопредельные" страны, имеющие общую границу, не были выкрашены в один цвет? Нетрудно начертить карту, для раскраски которой требуются лишь четыре краски. Зная только элементарную математику, вполне можно разобраться в строгом доказательстве того, что пять красок достаточно для раскраски любой карты. Можно ли утверждать, что для тех же целей необходимо и достаточно взять четыре краски? Иначе говоря, можно ли начертить карту, для раскраски которой необходимо иметь пять красок? Математики, размышлявшие над этой задачей, склоняются к мнению, что сделать этого нельзя, но утверждать с уверенностью невозможность построения карты, требующей для своей раскраски пяти цветов, они не могут.

Не проходит и месяца, чтобы кто-нибудь не прислал мне пространного "решения" проблемы четырех красок. Почти во всех случаях оказывается, что автор очередного "решения" спутал проблему с гораздо более простой задачей - доказательством того, что невозможно начертить карту, на которой было бы всего лишь пять стран и каждая из этих стран примыкала бы к четырем остальным странам (две страны, имеющие лишь одну общую точку, примыкающими друг к другу не считаются). Я сам тоже в какой-то мере способствовал этому распространенному заблуждению, написав как-то раз научно-фантастический рассказ под названием "Остров пяти красок" о вымышленном острове, который один польский тополог разделил на пять областей так, что каждая область имела общую границу с четырьмя остальными. Нетрудно доказать, что такую карту начертить нельзя. Можно предположить, что отсюда автоматически следует решение проблемы четырех красок для всех карт, но такое заключение неверно.

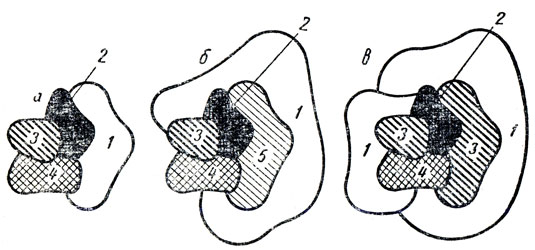
Рис. 221. При раскрашивании карты в четыре цвета часто приходится начинать всю работу сначала и выбирать другие краски. 1 - белый; 2 - черный; 3 - красный; 4 - серый; 5 - розовый

Чтобы разобраться, в чем здесь дело" рассмотрим простую карту, изображенную на рис. 221, а (истинная форма областей роли не играет, важно лишь то, как области примыкают друг к другу; проблема четырех красок потому и относится к топологии, что в ней речь идет о свойстве плоских фигур, не меняющемся при деформации поверхности, на которой эти фигуры начерчены). В какой цвет выкрасить еще не закрашенную область? Очевидно, цвет должен быть либо красным, либо каким-то новым, четвертым цветом, отличающимся от уже нанесенных на карту. Предположим, что мы избрали вторую альтернативу и выкрасили пустую область в зеленый цвет. Добавим теперь еще одну область. Вполне очевидно, что закончить раскраску карт (с соблюдением всех условий) без привлечения пятого цвета нельзя. Вернемся снова к карте и выкрасим пустую область вместо зеленого в красный цвет. Такая раскраска приводит к трудностям, если с первыми четырьмя областями соприкасаются две другие области (см. карту на рис. 221, в). Ясно, что для раскраски этих двух областей нам понадобятся четвертая и пятая краски. Является ли все сказанное доказательством того, что для раскраски некоторых карт необходимо брать пять красок? Отнюдь нет. В обоих случаях мы можем обойтись всего лишь четырьмя красками, следует только вернуться к исходной карте и изменить первоначальную схему раскраски.

При раскрашивании сложных карт с десятками "стран" мы то и дело будем попадать в подобные "тупики" и возвращаться к тому, с чего начали. Следовательно, для решения проблемы четырех красок необходимо либо доказать, что во всех случаях, изменив надлежащим образом схему раскраски, можно добиться успеха, либо придумать какой-нибудь способ, который позволил бы исключить все ненужные варианты раскраски любой карты в четыре цвета. Стифен Барр предложил замечательную топологическую игру, основанную на трудности предвидения таких "тупиковых" раскрасок. Игрок А чертит произвольную область. Игрок В раскрашивает ее и пририсовывает новую область. Игрок А раскрашивает новую область и добавляет еще одну область. Игра продолжается. Каждый из игроков раскрашивает область, начерченную противником, и дорисовывает свою область. Проигрывает тот, кто вынужден воспользоваться пятой краской. Я не знаю лучшего способа понять трудности, которые встречаются на пути решения проблемы четырех красок, чем просто поиграть в эту любопытную игру.

Часто говорят, первыми, кто понял, что для раскраски любой карты требуется взять лишь четыре краски, были картографы. Математик Кеннет О. Мэй усомнился в справедливости этого утверждения. Проведя тщательное исследование происхождения проблемы четырех красок, Мэй не нашел в старинных книгах по картографии ни формулировки проблемы, ни указания на то, что она известна авторам этих книг. По-видимому, впервые проблему четырех красок в явном виде сформулировал Фрэнсис Гетри, студент из Эдинбурга. Он упомянул о ней в письме брату Фредерику (ставшему впоследствии химиком), который в свою очередь сообщил ее (в 1852 году) своему преподавателю математику Августу де Моргану. Широкую известность проблема четырех красок приобрела после того, как в 1878 году выдающийся математик Артур Кэли сообщил, что он размышлял над этой проблемой, но так и не сумел ее решить.

В 1879 году английский юрист и математик Альфред Кемпе опубликовал то, что, по его мнению, было решением проблемы, а год спустя представил в журнал Nature статью со сверхсамоуверенным названием "Как раскрасить карту четырьмя красками". В течение десяти лет математики считали проблему решенной, но потом П. Дж. Хивуд указал на роковой пробел в доказательстве Кемпе. С тех пор математические умы безуспешно пытались найти решение проблемы. Внешне невинная формулировка проблемы четырех красок - кажется, что решить ее совсем нетрудно,- многим сулит ложные надежды. В своей автобиографической книге "Бывший вундеркинд" Норберт Винер писал о том, что и он, подобно всем математикам, пытался найти решение проблемы четырех красок, но каждый раз найденное решение, как заколдованное золото в волшебной сказке, обращалось в его руках в груду глиняных черепков. В настоящее время проблема четырех красок положительно решена для всех карт с числом стран, не превышающим 38. Может показаться, что 38 - очень маленькое число, но полученное решение становится менее тривиальным, если учесть, что число топологически различных карт с числом стран, не превышающим 38, оказывается больше чем 10³⁸. Даже современные быстродействующие электронно-вычислительные машины не в состоянии перебрать все эти варианты в сколько-нибудь разумный отрезок времени.

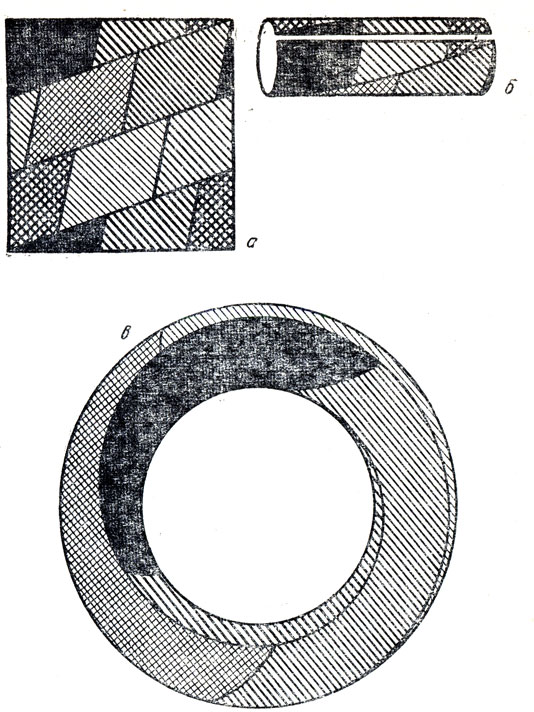
Рис. 222. Для раскраски карты на торе достаточно семи красок. Для получения тора лист бумаги (а) сворачивают в трубку (б), концы которой склеиваются (в) (тор показан в увеличенном виде)

Отсутствие доказательства для проблемы четырех красок на плоскости становится еще удивительнее, если учесть, что аналогичные проблемы решены для более сложных поверхностей (при рассмотрении проблемы четырех красок поверхность сферы не отличается от плоскости: любую карту на сфере можно превратить в эквивалентную карту на плоскости, сферу проколоть в точке, лежащей внутри любой области, а затем растянуть на плоскости). Для раскраски односторонних поверхностей, таких, как лист Мёбиуса, бутылка Клейна и проективная плоскость, необходимо и достаточно шести красок. Для раскраски карты на поверхности тора, или бублика, число красок должно быть равно семи. Одна из таких карт показана на рис. 222, е.

Обратите внимание на то, что каждая область ограничена шестью отрезками прямых и примыкает к шести другим областям. Проблема раскраски карты по сути дела решена для всех сколько-нибудь серьезно изученных сложных поверхностей, но стоит лишь взять поверхность, топологически эквивалентную плоскости или сфере, как решение проблемы ускользает от топологов. Хуже всего, что всякие видимые причины, объясняющие, почему так происходит, отсутствуют. Все предпринятые попытки, казалось, гарантировали успех, и лишь на самом последнем этапе, когда цепочка рассуждений вот-вот должна была замкнуться, обнаруживался досадный просчет, мнимый успех улетучивался подобно миражу. Трудно заранее предсказать, каким окажется решение знаменитой проблемы, но можно не сомневаться, что того, кто первым сумеет подтвердить или опровергнуть гипотезу о возможности раскраски любой карты четырьмя красками, ожидает всемирное признание и слава. "Прорыв" в неприступной обороне проблемы может произойти по одному из трех направлений:

1. Будет начерчена карта, для раскраски которой непременно требуются пять красок. "Если взять на себя смелость и составить прогноз на будущее,- пишет Г. С. М. Коксетер в великолепной статье "Проблема четырех красок, 1840-1890 годы",- то я должен высказать предположение, что карта, требующая для своей раскраски пяти красок, вполне может существовать, но даже простейшая из таких карт имеет столько стран (их могут быть сотни и даже тысячи), что ни у кого из тех, кто столкнется с ней, не хватит терпения, чтобы проделать все необходимые проверки и исключить возможность ее раскраски с помощью четырех красок".
2. Будет обнаружено доказательство гипотезы, может быть, с помощью какого-нибудь нового метода, который внезапно откроет многие запертые двери в здании математики.
3. Будет доказано, что доказать или опровергнуть гипотезу невозможно. Это утверждение может показаться странным, но в 1931 году Курт Гёдель установил, что во всякой дедуктивной системе, достаточно сложной для того, чтобы она включала арифметику, существуют математические теоремы, "неразрешимые" в рамках этой дедуктивной системы. До сих пор удалось доказать "неразрешимость" (в смысле Гёделя) лишь очень немногих великих гипотез. Является ли проблема четырех красок такого рода математической теоремой? Если это так, то ее можно считать "истинной" только в том случае, если ее или какую-нибудь другую тесно связанную с ней теорему включить в качестве нового недоказуемого постулата в расширенную дедуктивную систему.

К сожалению, доказательство того, что пяти красок достаточно для раскраски карт на плоскости, а шести или более красок необходимо и достаточно для раскраски некоторых более сложных поверхностей, слишком длинно, чтобы приводить его здесь. Некоторое представление о том, как протекает доказательство этих теорем, читатель сможет получить из следующего остроумного доказательства теоремы о раскраске в два цвета.

Рассмотрим все возможные карты на плоскости, образованные прямыми. Примером такой карты может служить обычная шахматная доска. Менее правильный узор изображен на рис. 223 слева. Достаточно ли двух красок для раскрашивания всех таких карт?

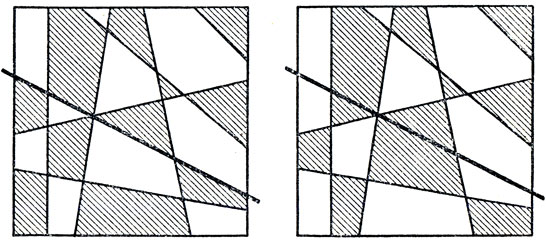
Рис. 223. Для раскраски любой карты, образованной прямыми, пересекающими всю ее поверхность от одного края листа до другого, достаточно двух красок

Оказывается, достаточно, и доказать это нетрудно. На любой правильно раскрашенной карте интересующего нас типа проведем еще одну прямую (например, жирную прямую на рис. 223 справа), разделив плоскость на две "карты". Каждая из новых карт в отдельности раскрашена правильно, но к новой "границе" только что проведенной прямой примыкают пары областей, окрашенных в один и тот же цвет. Для того чтобы восстановить правильную раскраску всей карты в целом, нужно перекрасить одну из карт-половинок (какую именно - безразлично), изменив окраску каждой из областей на противоположную. То, что при этом получится, показано на рис. 223 слева. Карта над черной прямой "обращена" - перекрашена так, словно "отрицательные" области стали "положительными" и наоборот, и, как нетрудно видеть, вся карта раскрашена правильно.

Рис. 224. Двух красок достаточно для раскрашивания карты, образованной либо линиями, идущими от одного края листа до другого, ибо замкнутыми кривыми

Для завершения доказательства рассмотрим плоскость, разделенную на две области одной-единственной прямой. Такую карту, разумеется, можно раскрасить два цвета. Проведем вторую прямую и раскрасим новую карту, переменив все цвета по одну сторону от новой прямой на противоположные. Затем проведем третью прямую и т. д. Ясно, что предложенный метод пригоден при любом числе прямых. Следовательно, "методом полой математической индукции" мы доказали теорему о возможности раскраски в два цвета всех карт, образованных прямыми на плоскости. Доказательство можно несколько обобщить на случай более разнообразных карт, например таких, как карта на рис. 224, образованная либо кривыми, пересекающими весь лист от одного края до другого, либо замкнутыми кривыми без самопересечений. Проведя еще одну кривую, пересекающую всю карту от одного ее края до другого, мы должны, как и прежде, изменить все цвета по одну сторону от кривой на противоположные. Если вновь проведенная кривая замкнута, то изменить нужно окраску всех областей, попавших внутрь кривой, или, если угодно, всех областей, оказавшихся снаружи. Замкнутые кривые могут иметь и точки самопересечения, но в этом случае перекрашивание областей более сложно.

Заметим, что на всех приведенных здесь двухцветных картах все вершины четны (напомним, что вершиной называется точка, в которой сходятся границы более двух стран), то есть в каждой вершине сходится четное число границ. Можно показать, что любую карту на плоскости можно раскрасить в два цвета тогда и только тогда, когда все ее вершины четны. Это утверждение известно как "теорема о двухцветных картах". Нетрудно видеть, что на торе эта теорема не выполняется. Для этого достаточно скатать в трубку квадратный лист бумаги, расчерченный на девять маленьких квадратов (наподобие игрового поля для крестиков и ноликов), а концы трубки склеить. Все вершины на таком "клетчатом" торе четны, но для его раскрашивания необходимо взять три краски.

Приведем теперь (скорее для развлечения, чем для уяснения существа дела) две задачи на раскрашивание карт. Они несложны, но в каждой имеется какая-нибудь ловушка, которая делает решение не столь легким, как это кажется с первого взгляда.

1. Стифен Барр сообщил мне в письме задачу о художнике, который хочет закончить большую абстрактную картину, изображенную на рис. 225. Он решил ограничиться четырьмя красками и каждую из областей окрасить только в один цвет, следя за тем, чтобы области, имеющие общую границу, не были окрашены одинаково. Площадь каждой области равна восьми квадратным футам, за исключением верхней области, имеющей вдвое большую площадь, чем остальные. Проверив запасы красок в тюбиках, художник обнаружил, что красной краски у него осталось ровно столько, сколько требуется, чтобы покрыть 24 квадратных фута, желтой хватит на покрытие такой же площади, зеленой - на 16 квадратных футов и синей - на 8 квадратных футов. Как ему следует поступить для того, чтобы закончить свою картину?
   
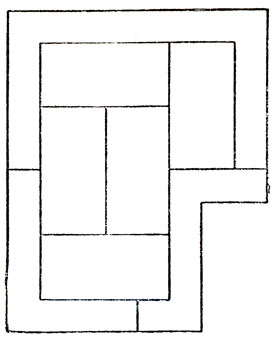
   Рис. 225. Сколько красок должен взять художник, чтобы раскрасить эту абстрактную картину?
   
   
2. Известный математик Лео Мозер предложил следующую задачу: как начертить на плоскости двухцветную карту, обладающую таким свойством, что, как бы вы ни накладывали на нее равносторонний треугольник со стороной 1, все три его вершины не должны лежать на точках одного цвета?

Утверждение о том, что на плоскости нельзя начертить пять областей так, чтобы любые две из них имели общую границу, было высказано в 1840 году Мёбиусом на одной из его лекций. Мёбиус придал ему форму притчи о восточном правителе, завещавшем свое царство пяти сыновьям при условии, если те сумеют так поделить наследство, чтобы владения каждого из сыновей граничили с владениями всех остальных. Эта задача эквивалентна следующей задаче из теории графов: можно ли так разместить на плоскости пять точек, чтобы они соединялись не пересекающимися друг с другом отрезками прямых? Доказательство того, что этого сделать нельзя, нетрудно, и его можно найти в любой книге по элементарной теории графов^*.

^* (Н. Тietzе, Famous Problems of Mathematics, Graylock Press, 1965, pp. 64-89.)

Неточность выражений, употребленных мной при обсуждении проблемы четырех красок как утверждения, неразрешимого в смысле Гёделя, послужила причиной следующего письма.

Уважаемая редакция!

Статья Мартина Гарднера о проблеме четырех красок доставила мне много удовольствия. Действительно, невозможно доказать, что доказать эту теорему невозможно. В самом деле, если утверждение теоремы (речь идет о теореме, утверждающей, что четырех красок достаточно для раскрашивания любой карты) ложно, то это, вне всяких сомнений, можно наглядно продемонстрировать, предъявив карту, которую нельзя раскрасить в четыре краски. Следовательно, если теорема недоказуема, то она должна быть верна. Это и означает, что мы не можем доказать, что доказать ее невозможно, ибо такое доказательство было бы эквивалентно доказательству теоремы и мы пришли бы к противоречию.

Аналогичное замечание применимо к любой теореме, ложность которой можно было бы продемонстрировать с помощью контрпримера, в частности к великой теореме Ферма. Такие теоремы могут быть недоказуемыми, но лишь в лом случае, если они истинны. Поэтому мы никогда не можем знать, что они недоказуемы, и математики должны вновь и вновь предпринимать попытки доказать их. Ситуация складывается просто ужасная! Хорошим выходом из нее могло бы послужить обращение к физике, но "гёделевщина" может вторгнуться и в эту область...

Ситуация станет менее ужасной, если учесть, что теорема, неразрешимая в смысле Гёделя в рамках данной дедуктивной системы, всегда может быть разрешена средствами метаматематики в расширенной системе. Если когда-нибудь будет доказано, что проблема четырех красок неразрешима в смысле Гёделя в рамках дедуктивной системы, опирающейся на определенные постулаты топологии и теории множеств, то она автоматически станет "истинной" (как объяснил нам Сиама), но "истинной" в метаматематическом смысле, то есть разрешимой в некоторой более широкой дедуктивной системе, может быть, в системе, в которую утверждение о возможности раскраски любой карты четырьмя красками само входит в качестве нового постулата.

Смешав всю имеющуюся у него синюю краску с третью всего количества красной краски, художник получил столько пурпурной краски, что ее хватило для закрашивания шестнадцати квадратных футов полотна. После того как большая область в верхней части абстрактной картины (рис. 225) и центральная область закрашены в желтый цвет, раскрасить остальные области в красный, зеленый и пурпурный цвета уже нетрудно.

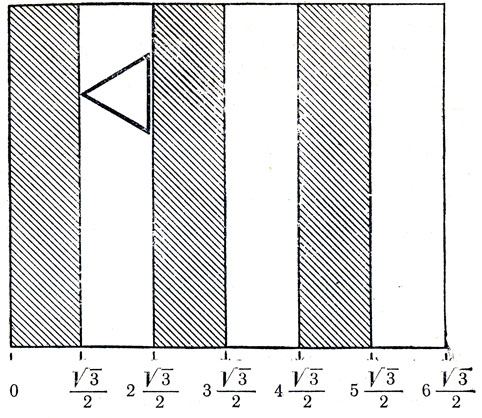
Рис. 226. Решение задачи о треугольнике и двуцветной карте

Раскрасить плоскость в два цвета так, чтобы вершины наложенного на нее равностороннего треугольника со стороной в 1 при любой его ориентации не попадали на три точки одного цвета, проще всего так: нужно разделить плоскость на параллельные полосы, каждая шириной в √3/2 единиц, а затем попеременно раскрасить их в черный и белый цвета так, как показано на рис. 226. Чтобы "полосатая" плоскость давала решение задачи, необходимо ввести понятие открытого и замкнутого множеств. Континуум вещественных чисел, например чисел, заключенных между 0 и 1, называется замкнутым интервалом, если 0 и 1 принадлежат ему, и открытым интервалом, если 0 и 1 не принадлежат ему. Если интервал включает один из своих концов (0 или 1) и не включает другого, то говорят, что он замкнут с одного и открыт с другого конца.

Полосы на карте будем считать замкнутыми слева и открытыми справа. Самая левая черная полоса начинается с отметки 0 (внизу) и доходит до отметки √3/2,- но не включает эту отметку. Следующая (белая) полоса включает отметку √3/2 и доходит до отметки 2 (√3/2), не включая ее, и т. д. Иначе говоря, каждая вертикальная линия на карте принадлежит лишь той полосе, которая расположена справа от нее. Это необходимо для соблюдения условий задачи в тех случаях, когда все три вершины треугольника (рис. 226) должны были бы располагаться на границах между полосами.

Л. Мозер, приславший эту задачу, сообщает, что ему не известно, во сколько цветов нужно раскрасить плоскость для того, чтобы концы единичного отрезка не лежали на точках одного и того же цвета. Было доказано, что четыре краски необходимы, а семи красок достаточно. (То обстоятельство, что семи красок достаточно, видно из рассмотрения правильной мозаики, выложенной из шестиугольников, если взять радиус описанной вокруг каждого шестиугольника окружности чуть больше единицы и окрасить их так, чтобы цвета любого шестиугольника и шести окружающих его шестиугольников были различными.) Разрыв между четырьмя красками (необходимое условие) и семью красками (достаточное условие) настолько велик, что задача, по-видимому, еще долгое время не будет решена.