Глава 20. Девять задач

1. Сцепленные болты. Два одинаковых болта сцеплены нарезкой (рис. 109). Взяв их покрепче за головки, чтобы они не могли проворачиваться, обведите несколько раз один болт вокруг другого в направлении, указанном стрелками (повертев перед этим большими пальцами рук, вы сможете наглядно представить себе движение болтов).

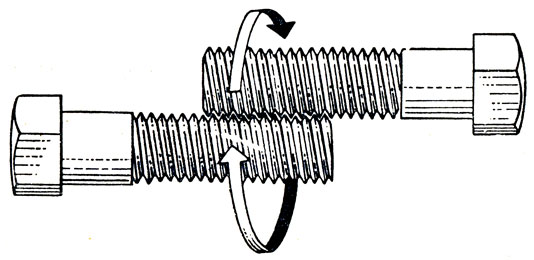
Рис. 109. Сцепленные болты

Будут ли головки болтов:

• сближаться,
• расходиться
• оставаться на неизменном расстоянии друг от друга?

Использовать при решении задачи настоящие болты не разрешается.

2. Кругосветный полет. Группа самолетов базируется на небольшом острове. Баки каждого самолета вмещают столько топлива, что его хватает на облет половины земного шара. При Заправке в воздухе из баков одного самолета в баки другого можно перекачивать любое количество горючего. На земле заправку можно производить только на острове. Для удобства решения задачи предполагается, что заправка на земле и в воздухе происходит мгновенно, без потерь времени.

Чему равно минимальное число самолетов, которые смогут обеспечить полет одного самолета по большому кругу, если считать, что скорость и расход топлива у всех самолетов одинаковы и все самолеты благополучно возвращаются на свою базу?

3. Окружность на шахматной доске. Сторона клетки на шахматной доске равна 4 см. Чему равен радиус наибольшей окружности, которую можно провести на шахматной доске так, чтобы она проходила только по черным клеткам?

4. Универсальная пробка. Во многих сборниках головоломок объясняется, как вырезать пробку, которой можно плотно заткнуть квадратное, круглое и треугольное отверстия (рис. 110). Не менее интересно вычислить объем такой пробки. Предположим, что радиус ее круглого основания равен единице длины, высота - двум единицам и что ребро в ее верхней части (имеющее в длину также две единицы) расположено строго над одним из диаметров основания и параллельно ему. Все параллельные сечения пробки, плоскость которых перпендикулярна верхнему ребру, имеют вид треугольников.

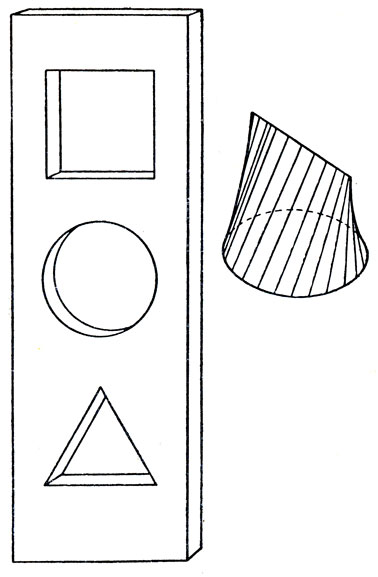
Рис. 110. Универсальная пробка

Поверхность пробки можно рассматривать как образованную прямыми, соединяющими точки верхнего, прямолинейного, и нижнего ребра, имеющего форму окружности. Каждая прямая параллельна одной из плоскостей, перпендикулярных верхнему ребру.

Разумеется, объем пробки нетрудно вычислить методами анализа, но найти его можно и более простым способом, зная лишь, что объем прямого цилиндра равен произведению площади его основания на высоту.

5. Повторяющееся число. Если у вас соберутся гости, вы сможете удивить их необычным фокусом. Попросите одного из гостей - назовем его А - написать на листке бумаги какое-нибудь трехзначное число два раза подряд, чтобы получилось шестизначное число (например, 394 394). Отвернитесь так, чтобы вы не могли видеть написанное число, и попросите А передать листок другому гостю В, которого попросите разделить число на 7.

"Об остатке не беспокойтесь, его не будет",- говорите вы гостю В, и он с удивлением убеждается, что вы правы (например, 394 394 при делении на 7 дает 56 342). Не сообщая вам результат, В передает листок бумаги третьему гостю С, который делит полученный В результат на 11. Вы снова утверждаете, что остатка не будет, и снова оказываетесь правы (56 342 при делении на 11 дает 5122).

Не оборачиваясь к гостям и не зная, какие цифры написаны на листке бумаги, вы просите передать его четвертому гостю D который должен поделить последний результат на 13. Снова деление происходит без остатка (5122 при делении на 13 дает 394). Окончательный результат D записывает на клочке бумаги и, сложив его, передает вам. Не разворачивая листка с ответом, вы передаете его А и говорите: "Разверните листок и вы увидите свое трехзначное число".

Докажите, что фокус получается всегда, независимо от того, какое число выберет первый гость.

6. Столкновение ракет. Две ракеты летят навстречу друг другу, одна - со скоростью 9000 миль/час, а другая - со скоростью 21000 миль/час. Их стартовые площадки находятся на расстоянии 1317 миль одна от другой: Не пользуясь карандашом и бумагой, подсчитайте, какое расстояние будет между ракетами за минуту до столкновения.

7. Как передвинуть монеты. На ровной гладкой поверхности (например, на столе) выложен треугольник из шести монет (рис. 111). Требуется за наименьшее число ходов передвинуть монеты так, чтобы они образовали кольцо, показанное на рис. 111 внизу. Каждый ход состоит в передвижении только одной монеты. Сдвигать при этом с места другие монеты нельзя. В новом положении каждая монета должна касаться двух других монет. Поднимать монеты с поверхности при решении задачи не разрешается.

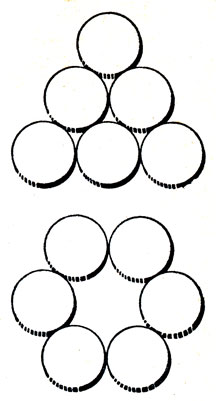
Рис. 111. Как передвинуть монеты?

8. Рукопожатия и графы. Докажите, что число участников последнего конгресса биофизиков, обменявшихся рукопожатиями нечетное число раз, четно. Та же задача допускает и графическую интерпретацию. На листе бумаги поставьте любое число точек (каждая точка изображает участника конгресса). Между любыми двумя точками разрешается проводить сколько угодно линий. Каждая точка может неограниченное число раз "обмениваться рукопожатиями" с другими точками или быть необщительной и не здороваться ни с кем. Докажите, что число точек, из которых исходит нечетное число линий, четно.

9. Необычная дуэль. Смит, Браун и Джонс, решив внести в обычную дуэль на пистолетах некоторое разнообразие, условились провести поединок по несколько измененным правилам. Вытащив жребий и узнав, кому из них выпало стрелять первым, кому - вторым и кому - третьим, они разошлись по своим местам, встав в вершинах равностороннего треугольника. Договорились, что каждый по очереди производит лишь один выстрел и может целиться в кого угодно. Дуэль продолжается до тех пор, пока не будут убиты любые два ее участника. Очередность стрельбы определяется только результатами жеребьевки и остается неизменной в течение всего поединка.

Все три участника знают своих противников. Смит никогда не промахивается, Браун попадает в. цель в 80% случаев, а Джонс, стреляющий хуже всех, промахивается так же часто, как и попадает в цель.

Кто из дуэлянтов имеет более высокий шанс уцелеть, если считать, что все трое придерживаются оптимальных стратегий и никто из них не будет убит шальной пулей, предназначенной другому? Более трудный вопрос: чему равна вероятность остаться в живых для каждого из дуэлянтов?

1. Головки болтов не сближаются и не расходятся. Движение болтов можно сравнить с движением человека, идущего вверх по спускающемуся эскалатору со скоростью эскалатора.

2. Для обеспечения кругосветного полета одного самолета достаточно двух самолетов. Сделать это можно многими способами. Способ, предлагаемый нами, по-видимому, наиболее экономичен: расходуется лишь пять заправок горючего, пилоты двух обеспечивающих полет самолетов успевают перед вылетом с базы выпить по чашке кофе и перехватить по бутерброду, а весь метод обладает не лишенной приятности симметрией.

Самолеты А, В и С стартуют одновременно. Пролетев ¹/₈ намеченного расстояния (то есть длины окружности большого круга), С перекачивает ¹/₄ исходного запаса горючего в баки А и ¹/₄ - в баки В, после чего у него остается ¹/₄ заправки. Этого количества горючего ему хватает, чтобы вернуться на базу.

Самолеты А и В, продолжая полет, проходят еще ¹/₈ кругосветного маршрута, после чего В перекачивает ¹/₄ заправки в баки А. Баки В остаются заполненными ровно наполовину, и он благополучно дотягивает до родного аэродрома, совершая посадку уже с пустыми баками.

Полностью заправленный самолет А продолжает лететь до тех пор, пока у него не кончится горючее. К этому моменту он находится на расстоянии ¹/₄ всего пути от базы, и его встречает самолет С, успевший перезаправиться на острове. С перекачивает в баки А ¹/₄ заправки и вслед за А берет курс на базу. На расстоянии ¹/₈ окружности земного шара горючее у А и С кончается, но тут их встречает побывавший на базе,В, который отдает каждому из них по ¹/₄ полной заправки. После этого топлива в баках каждого самолета хватает как раз на то, чтобы благополучно вернуться на свою базу (правда, садиться приходится с пустыми баками).

Графически весь полет можно изобразить с помощью диаграммы, показанной на рис. 112, где по горизонтальной оси отложено расстояние, а по вертикальной - время. Правый и левый края диаграммы следует считать склеенными.

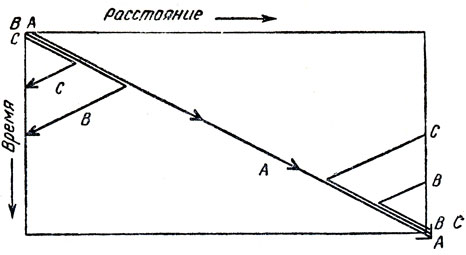
Рис. 112. Кругосветный полет

Взяв раствор циркуля равным квадратному корню из 20 см и поставив его острие в центр черной клетки на шахматной доске с четырехсантиметровыми клетками, вы сможете описать наибольшую из окружностей, проходящих только по черным клеткам.

4. Любое поперечное сечение пробки плоскостью, перпендикулярной верхнему ребру и основанию, имеет вид треугольника. Если бы пробка была цилиндрической, соответствующие сечения были бы прямоугольниками, при этом площадь каждого прямоугольного сечения была бы вдвое больше площади треугольного сечения. Поскольку цилиндр можно считать составленным из прямоугольных поперечных сечений, объем универсальной пробки должен составлять половину объема цилиндра: объем цилиндра равен 2π, следовательно, объем универсальной пробки равен π.

В действительности же существует бесконечно много пробок различной формы, которыми можно заткнуть все три отверстия. Пробка той формы, которая описана в условии задачи, имеет наименьший объем по сравнению с любым выпуклым телом, способным заткнуть те же три дырки. Пробку наибольшего объема нетрудно получить, если обрезать цилиндрическую пробку так, как показано на. рис. 113. Именно эту форму пробки обычно имеют в виду составители сборников головоломок, предлагая читателям найти универсальную затычку, подходящую к круглому, треугольному и квадратному отверстиям. Ее объем равен 2π - ⁴/₃.

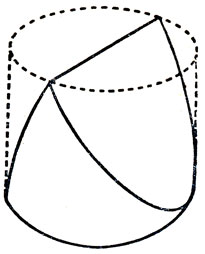
Рис. 113. Как сделать универсальную пробку наибольшего объема

5. Написать подряд два раза трехзначное число - все равно что умножить это число на 1001. Число 1001 разлагается на простые множители 7, 11 и 13, поэтому, приписав к трехзначному числу его же еще раз справа, задумавший просто умножает свое число на 7×11×13. Разделив шестизначное число на 7, 11 и на 13, он, естественно, получает снова исходное трехзначное число. Эта задача заимствована из книги Я. И. Перельмана^*.

^* (Я. И. Перельман, Живая математика, изд. 9, М, изд-во "Наука", 1970.)

6. Две ракеты сближаются со скоростью 30 000 миль/час, или 500 миль/мин. Отсчитывая время назад, от момента столкновения, мы получаем, что за минуту до столкновения ракеты должны были бы находиться на расстоянии 500 миль друг от друга.

7. Рассмотрим исходное расположение монет в виде треугольника. Обозначим цифрой 1 верхнюю монету, цифрами 2 и 3 - монеты в следующем ряду и цифрами 4, 5, 6 - монеты в нижнем ряду. Следующие четыре хода позволяют получить представление о множестве других решений: передвинем монету 1 так, чтобы она коснулась 2 и 4; монету 4 передвинем так, чтобы она коснулась 5 и 6; монету 5 передвинем так, чтобы она коснулась монет 1 и 2 снизу, и, наконец, монету 1 передвинем так, чтобы она коснулась монет 4 и 5.

8. Поскольку в каждом рукопожатии участвуют двое людей, полное число рукопожатий, которыми обменялись все участники конгресса, делится на 2 и поэтому четно. Число рукопожатий, приходящихся на долю тех, кто обменялся со своими коллегами четным числом рукопожатий, очевидно, четно. Только сумма четного числа нечетных слагаемых может быть четным числом, поэтому число тех участников конгресса, которые обменялись с другими участниками нечетным числом рукопожатии, четно.

То же утверждение можно доказать и иным путем. Перед началом работы конгресса число его участников, обменявшихся нечетным числом рукопожатий, равно 0. После первого рукопожатия появляются два "нечетных участника". Все рукопожатия, начиная со второго, делятся на три типа: рукопожатия между двумя "четными" участниками, рукопожатия между двумя "нечетными" участниками и "смешанные" рукопожатия между "четными" и "нечетными" участниками. Каждое "четно-четное" рукопожатие увеличивает число "нечетных" участников на 2. Каждое "нечетно-нечетное" рукопожатие уменьшает число "нечетных" участников также на 2. Каждое "нечетно-четное" рукопожатие превращает "нечетного" участника в "четного" и, наоборот, "четного" участника в "нечетного" и, таким образом, оставляет число "нечетных" участников без изменения. Поэтому четное число биофизиков, обменявшихся нечетным числом рукопожатий, не может изменить своей четности и должно всегда оставаться четным.

Оба доказательства применимы к графу, на котором линии связывают точки попарно. Линии графа образуют сеть. Число точек сети, из которых выходит нечетное число линий, четно. Эта теорема встретится нам еще раз в главе 22 при рассмотрении головоломок, связанных с блужданием по сети линий.

9. Наибольшую вероятность выжить в "треугольной" дуэли имеет худший из стрелков, Джонс. Следом за ним идет Смит, который никогда не промахивается. По-скольку противники Джонса, когда настает их очередь стрелять, целятся друг в друга, оптимальная стратегия для Джонса заключается в том, чтобы стрелять в воздух до тех пор, пока один из его противников не будет убит. После этого он стреляет в оставшегося противника, имея перед ним большое преимущество.

Легче всего подсчитать вероятность остаться в живых для Смита. В дуэли с Брауном с вероятностью ¹/₂ он стреляет первым. В этом случае он убивает Брауна. Браун, который попадает в цель в 4 случаях из 5, стреляет первым также с вероятностью ¹/₂. В этом случае Смит остается в живых с вероятностью ¹/₅. Таким образом, Смит с вероятностью ¹/₂ + ¹/₂×¹/₅ = ³/₅ переживает Брауна. Если Смит остается в живых, то в него стреляет Джонс, который в ¹/₂ всех случаев промахивается. Но если Джонс промахивается при своем первом выстреле, то Смит, дождавшись своей очереди стрелять, убивает его. Поэтому с вероятностью ¹/₂ Смит выходит из дуэли с Джонсом живым и невредимым. Итак, вероятность остаться в живых после дуэли с обоими своими противниками для Смита равна ³/₅×¹/₂ = ³/₁₀.

Случай с Брауном более сложен, потому что требует рассмотрения бесконечного множества случаев. Вероятность остаться в живых после дуэли со Смитом для Брауна равна ²/₅ (мы только что показали, что Смит в дуэли с Брауном имеет вероятность уцелеть, равную ³/₅; так как в живых должен остаться лишь один из дуэлянтов, искомую вероятность для Смита мы находим, вычитая ³/₅ из 1). Затем в Брауна стреляет Джонс, который попадает в цель лишь в половине случаев. Если Джонс промахивается, то Браун с вероятностью ⁴/₅ убивает его. Итак, на этом этапе дуэли Браун с вероятностью ¹/₂×⁴/₅ = ⁴/₁₀ выходит победителем из поединка с Джонсом. Но с вероятностью ¹/₅ Браун может промахнуться, после чего Джонс имеет право выстрелить еще раз. С вероятностью ¹/₂ Браун останется в живых, и тогда он в свою очередь сможет выстрелить в Джонса и с вероятностью ⁴/₅ убить его. Шансы Брауна остаться в живых во время второго тура поединка составляют ¹/₂×¹/₅×¹/₂×⁴/₅ = ⁴/₁₀₀.

Если Браун снова промахнется, то во время третьего тура он может убить Джонса лишь с вероятностью ⁴/₁₀₀₀. В случае повторного промаха во время четвертого тура он попадет в Джонса с вероятностью ⁴/₁₀₀₀₀ и т. д. Таким образом, шансы Брауна пережить Джонса равны сумме бесконечного ряда

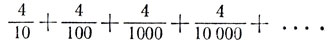
Это не что иное, как бесконечная периодическая десятичная дробь 0,44444..., равная ⁴/₉.

Ранее мы видели, что Браун с вероятностью ²/₅ может пережить Смита. Только что мы показали, что с вероятностью ⁴/₉ он останется в живых после дуэли с Джонсом. Вероятность того, что именно Браун переживет обоих своих противников, равна, следовательно, ²/₅×⁴/₉ = ⁸/₄₅.

Аналогичным способом можно было бы подсчитать и вероятность уцелеть для Джонса, но проще получить ее вычитанием из 1 соответствующих вероятностей для Смита ³/₁₀ и Брауна ⁸/₄₅. Она оказывается равной ⁴⁷/₉₀.

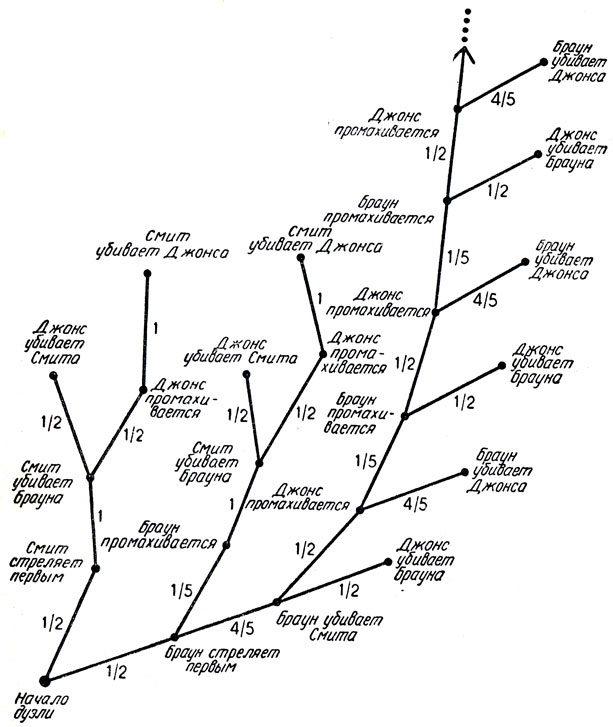
Рис. 114. Дерево дуэли Смита, Джонса и Брауна

Весь поединок удобно изобразить с помощью специального графа - дерева дуэли (рис. 114). Вначале ствол дерева раздваивается. Это происходит потому, что если первым стреляет Джонс, то он производит свой выстрел в воздух, после чего остаются две равновероятные возможности: стреляет либо Смит, либо Джонс (эти двое стреляют "вполне серьезно", с твердым намерением убить своего противника). Одна из ветвей дерева простирается до бесконечности. Подсчет вероятности для того или иного дуэлянта остаться в живых производится следующим образом:

1. Нужно отметить все ветви дерева, в которых интересующий нас участник поединка является единственным из всех троих, оставшихся в живых.
2. Идя от каждой из отмеченных ветвей назад к корню дерева, следует перемножить вероятности всех пройденных отрезков пути. Произведение даст вероятность события, соответствующего концу отмеченной ветви.
3. Сложить все вычисленные в п. 2 вероятности. Их сумма будет интересующей нас вероятностью выживания того или иного дуэлянта.

При вычислении вероятностей выжить для Брауна и Джонса приходится принимать во внимание бесконечно много ветвей, однако с помощью графа нетрудно указать формулу общего члена соответствующего ряда.

Различные варианты этой задачи включены во многие сборники головоломок.