Глава 18. Английский изобретатель головоломок Генри Э. Дьюдени

Генри Эрнест Дьюдени - величайший английский изобретатель головоломок. Трудно в наше время найти хоть одну книгу по занимательной математике, в которой (часто без указания авторства) не нашлось бы нескольких блестящих математических задач, рожденных неисчерпаемой фантазией Дьюдени.

Дьюдени родился в небольшой английской деревушке Мэйфилд в 1857 году и, следовательно, был на 16 лет моложе американского гения головоломок Сэма Лойда. Не знаю, встречались ли когда-нибудь эти мастера головоломки лично, но в 90-х годах прошлого века они успешно сотрудничали в английском журнале Tit-Bits ("Лакомые кусочки"), публикуя в нем серию статей с математическими головоломками, а позднее условились обмениваться своими находками, помещая их в отделах математических игр и головоломок различных газет и журналов. Этим и объясняется большое число совпадений и повторений в публикациях Лойда и Дьюдени.

Очевидно, Дьюдени был лучшим математиком, чем Лойд. Но Лойд с непревзойденным мастерством умел поразить воображение широкой публики остроумными игрушками и различного рода рекламными трюками. Ни одно из творений Дьюдени никогда не достигало такой поистине мировой известности, какой пользовалась лойдовская игра в пятнадцать или головоломка "Таинственное исчезновение", в которой один из нарисованных по кругу китайских воинов исчезал буквально на глазах зрителей. С другой стороны, произведения Дьюдени отличались большей математической глубиной и тонкостью (однажды Дьюдени назвал ребусы и загадочные картинки, которые Лойд выпускал тысячами, "детской забавой, представляющей интерес лишь для слабоумных"). Подобно Лойду, Дьюдени любил облекать свои задачи в форму забавных анекдотов. В этом ему, по-видимому, оказывала помощь его жена Алиса, написавшая более 30 романов, пользовавшихся в свое время огромной популярностью. Дьюдени принадлежат шесть сборников головоломок (три из них составлены после его смерти, последовавшей в 1931 году). И по сей день они остаются непревзойденными шедеврами занимательной математической литературы.

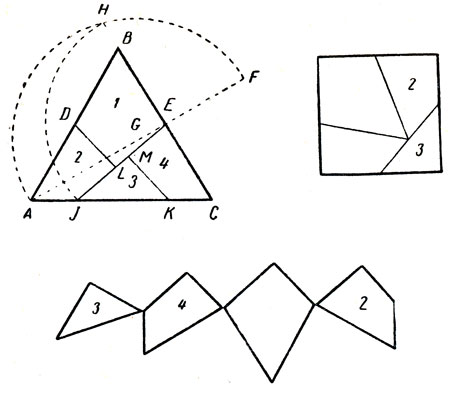
Рис. 101. Одна из головоломок Дьюдени. Как разрезать равносторонний треугольник, чтобы из его частей можно было составить

Первая книга Дьюдени "Кентерберийские головоломки" вышла в свет в 1907 году. По замыслу автора она должна была состоять из серии головоломок, которые по очереди рассказывают те самые пилигримы, чьи истории поведал нам Чосер^*. "Не стану объяснять, сколь необычным путем эти головоломки попали ко мне в руки,- писал Дьюдени,- а сразу приступлю к делу... чтобы предоставить моим читателям возможность испробовать свои силы в их решении". Помещенная в этой книге задача галантерейщика принадлежит к числу наиболее известных геометрических находок Дьюдени. Задача состоит в том, чтобы разрезать равносторонний треугольник на четыре части, из которых можно было бы составить квадрат (рис. 101). Разделим стороны АВ и ВС пополам в точках D и Е. На продолжении отрезка АЕ за точку Е отложим отрезок EF, равный ЕВ. Разделив отрезок AF пополам, опишем дугу AHF с центром в точке G - середине отрезка AF. Продолжим сторону СВ за вершину В до пересечения с проведенной только что дугой в точке Я. Из точки Е как из центра опишем дугу HJ. На стороне АС отложим отрезок JK, равный BE. Из точек D и К опустим перпендикуляры на EJ. Их основания обозначим через L и М. В правом верхнем углу на рис. 101 показано, как следует расположить части треугольника, чтобы составить из них идеальный квадрат. Если получившиеся при разрезании четыре фигуры скрепить между собой в трех вершинах так, как показано на рис. 101 внизу, то они образуют цепочку, которая при складывании по часовой стрелке даст треугольник, а при складывании против часовой стрелки - квадрат. Выступая в 1905 году с докладом о своей задаче перед Лондонским королевским обществом, Дьюдени демонстрировал решение на модели из красного дерева с бронзовыми шарнирами.

^* (Дж. Чосер, Кентерберийские рассказы, М., Гослитиздат, 1946.)

Теорема, впервые доказанная известным немецким математиком Давидом Гильбертом, утверждает, что любой многоугольник, если разрезать его на конечное . число частей, можно превратить в любой другой многоугольник, равновеликий первому. Доказательство этой теоремы длинно, но несложно. Оно основано на двух фактах:

1. всякий многоугольник при разрезании его по диагоналям распадается на конечное число треугольников;
2. всякий треугольник можно разрезать на конечное число частей, из которых можно составить прямоугольник с заранее заданным основанием.

Это означает, что любой многоугольник самой причудливой формы мы всегда можем превратить в прямоугольник с заданным основанием, если проделаем три операции: разрежем исходный многоугольник на треугольники; разрежем треугольники на части, сложив из этих частей прямоугольники с заданным основанием, равновеликие треугольникам; наконец, прямоугольники с одинаковым (заданным) основанием объединим в один большой прямоугольник с тем же основанием. Производя названные три операции в обратном порядке, мы сможем превратить построенный большой прямоугольник в любой другой равновеликий ему многоугольник.

Совершенно неожиданным является тот факт, что аналогичной теоремы для многогранников - объемных тел, ограниченных плоскими, многоугольниками,- не существует. Не существует также и общего метода, который позволил бы нам рассечь плоскостями любой многогранник так, чтобы из получившихся частей можно было сложить любой другой многогранник равного объема, хотя в отдельных частных случаях эта задача вполне разрешима. От надежды найти общий метод пришлось отказаться еще в 1900 году, когда было доказано, что призму нельзя рассечь так, чтобы из ее частей можно было составить равный по объему тетраэдр.

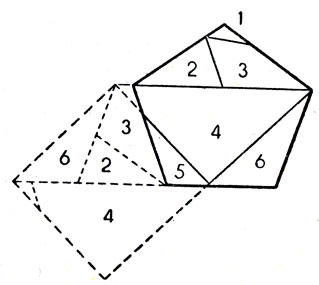
Рис. 102. Как составить квадрат из разрезанного пятиугольника

Хотя метод Гильберта гарантирует возможность превращения одного многоугольника в другой с помощью конечного числа разрезов, число получающихся при этом частей может быть очень велико. Изящное решение предполагает использование минимального числа частей. Найти такой минимум часто бывает весьма трудно. В тонком искусстве геометрических построений Дьюдени неизменно сопутствовал успех, и ему часто удавалось улучшать рекорды, незыблемо державшиеся в течение долгих лет. Например, долгое время считали, что превратить правильный пятиугольник в квадрат можно лишь в том случае, если мы разрежем пятиугольник по крайней мере на семь частей, хотя для превращения в квадрат правильного шестиугольника его достаточно разрезать на пять частей. Дьюдени удалось превратить правильный пятиугольник в квадрат, разрезав его всего лишь на шесть частей. Этот рекорд остается непревзойденным и поныне. Решение Дьюдени показано на рис. 102. Если кто-нибудь заинтересуется тем, каким образом Дьюдени напал на свой метод, ему следует обратиться к книге Дьюдени "Математические забавы"^*.

^* (Т. Е. Dudeney, Amusements in Mathematics, London, 1917.)

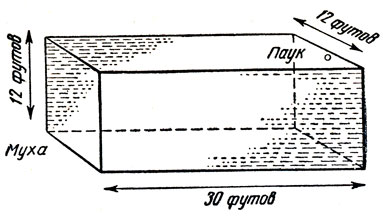
Рис. 103. Задача о пауке и мухе

Наиболее известная головоломка Дьюдени - задача о пауке и мухе - представляет собой элементарную, но весьма изящную задачу из геометрии геодезических^*. Впервые она была опубликована в 1903 году в одной английской газете, но внимание широкой публики привлекла лишь два года спустя, после того как ее перепечатала лондонская газета "Дейли мейл". Комната имеет форму прямоугольного параллелепипеда, размеры которого указаны на рис. 103. Посредине боковой стены на расстоянии одного фута от потолка сидит паук. Посредине противоположной стены на высоте одного фута от пола сидит муха. От страха у нее отнялись ноги, и она не может двинуться с места. Спрашивается, каково кратчайшее расстояние, которое должен преодолеть паук для того, чтобы схватить муху?

^* (Дать в нескольких словах простое и строгое определение геодезической довольно трудно. Обычно (хотя это и не совсем верно) геодезическими называют кратчайшие линии на поверхности. Более подробно о геодезических можно прочитать в брошюрах Л. А. Люстерника "Геодезические линии" (Гостехтеоретиздат, 1940) и "Кратчайшие линии" (Гостехтеоретиздат, серия "Популярные лекции по математике", вып. 19, 1955).- Прим. перев.)

Для решения задачи нужно построить развертку граней прямоугольного параллелепипеда и провести на ней прямую от местонахождения паука к точке, в которой сидит муха. Поскольку построить развертку можно многими способами, найти кратчайшее расстояние не так легко, как кажется на первый взгляд.

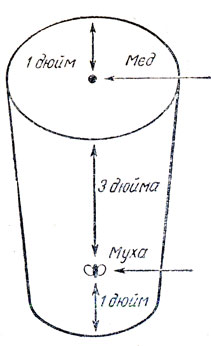
Рис. 104. Задача о мухе и капле меда

В менее известной задаче Дьюдени, также связанной с построением геодезической, речь идет о цилиндрическом стакане (рис. 104), имеющем четыре дюйма в высоту и шесть дюймов по окружности. Внутри него на расстоянии одного дюйма от верхнего края на стенке имеется капелька меда. Снаружи на стенке, прямо против капельки, на расстоянии одного дюйма от дна стакана сидит муха. Каков кратчайший путь от мухи к меду? Какое расстояние должна пройти муха, следуя кратчайшим путем к любимому лакомству?

Интересно отметить, что, хотя Дьюдени был мало знаком с топологией, в его время еще только начинавшей развиваться, при решении различных головоломок, связанных с отысканием кратчайших путей или размещением фигур на шахматной доске, он нередко пользовался остроумными топологическими приемами. Одним из таких приемов является его "метод нити и пуговиц". Существо этого метода хорошо можно понять на примере старинной шахматной задачи, изображенной на рис. 105. Как поменять местами черных и белых коней за наименьшее число ходов? Заменим восемь внешних квадратов доски восемью пуговицами, а все возможные ходы каждого коня отметим прямыми, соединяющими начальную и конечную позиции (на рис. 105 это показано на средней схеме). Представим себе теперь, что эти прямые - не что иное, как нити, связывающие пуговицы. Очевидно, что эти нити, не меняя топологической структуры и связности схемы, можно распутать и расположить пуговицы по окружности (на рис. 105 такое расположение показано внизу). Теперь сразу видно, что для решения задачи нужно лишь, записывая ходы (чтобы потом воспроизвести их на шахматной доске), переставлять коней в любом направлении по кругу до тех пор, пока они не поменяются местами. То, что поначалу казалось сложным, метод нити и пуговиц делает до смешного простым.

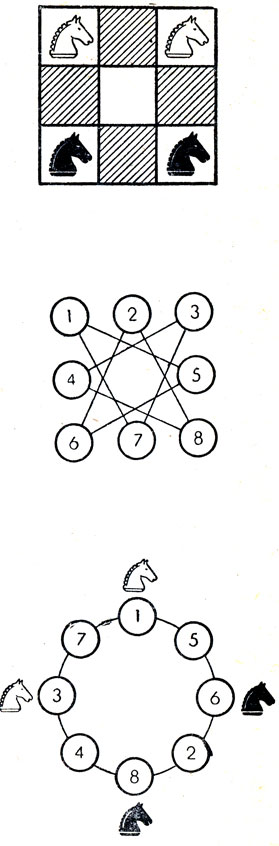
Рис. 105. Изобретенный Дьюдени 'метод нити и пуговиц'

Многие задачи Дьюдени относятся к теории чисел. Наиболее трудную из них сформулировал доктор медицины из "Кентерберийских головоломок". У почтенного доктора было два сферических сосуда, один из них имел в окружности ровно фут, другой - два фута. Доктору хотелось выяснить точную величину двух других сосудов той же формы, но иных размеров, которые вмещали бы столько же жидкости, сколько первые два сосуда.

Поскольку объемы сосудов, имеющих одинаковую форму, но отличающихся размерами (в геометрии такие фигуры называются подобными), относятся как кубы соответствующих линейных размеров, задача сводится к решению диофантова уравнения х³ + y³ = 9 в рациональных числах, отличных от 1 и 2. Два таких числа, разумеется, должны быть дробными. Дьюдени нашел дроби

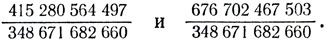
Знаменатели и первой и второй дроби оказались короче ранее известных. Если учесть, что Дьюдени не пользовался современной цифровой вычислительной машиной, то этот факт достоин удивления.

Любителям такого рода задач доставит удовольствие и более простое исследование: найти два рациональных числа, сумма кубов которых равна 6. Французский математик прошлого века Андриен Мари Лежандр доказал, что таких дробей не существует, однако Дьюдени опроверг его "доказательство" и сумел найти решение. Числители и знаменатели найденных Дьюдени дробей всего лишь двузначны!

Задаче Дьюдени о треугольнике, который нужно разрезать так, чтобы из его частей можно было составить квадрат, было посвящено много писем читателей. Оказалось, что метод Дьюдени после некоторых изменений приложим не только к равносторонним треугольникам, но и к более широкому классу треугольников. Одна читательница сообщила, что задача Дьюдени навела ее сына на мысль сделать набор из четырех столиков, которые при желании можно составить так, чтобы крышки образовывали либо квадрат, либо равносторонний треугольник. Столики всем очень понравились. Другой читатель, воспользовавшись решением Дьюдени, разбил плоскость на бесконечную мозаику из взаимозацепляющихся квадратов и равносторонних треугольников.

Некоторые читатели, ошибочно полагая, что точки J и K (на рис. 101) расположены непосредственно под точками D и E, прислали доказательства того, что из четырех частей треугольника нельзя составить точный квадрат. Но по построению точки J и K не совпадают с основаниями перпендикуляров, опущенных из D и E. Строгое доказательство точности решения Дьюдени можно найти в статье Честера У. Хоули "Еще одна заметка о превращении квадрата в равносторонний треугольник"^*.

^* (Mathematics Teacher, February 1960.)

Интересный вариант задачи Дьюдени о пауке и мухе опубликовал Морис Крайчик. Восемь пауков отправляются на охоту из точки, расположенной на 80 дюймов выше центра торцовой стенки комнаты, имеющей форму прямоугольного параллелепипеда. Каждый из них, следуя своим маршрутом, направляется к мухе, сидящей в точке, расположенной на 80 дюймов ниже центра противоположной стенки комнаты. Каждый паук движется со скоростью 0,65 мили в час. По истечении 625/11 секунды все пауки одновременно настигают муху. Каковы размеры комнаты?

Длина кратчайшего пути от паука к мухе равна 40 футам, как видно из развертки комнаты, показанной на рис. 106. Интересно заметить, что эта геодезическая пересекает 5 из 6 граней развертки.

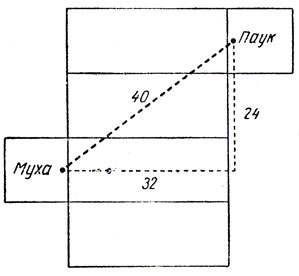
Рис. 106. Ответ к задаче о пауке и мухе

Муха доползает до капли меда, пройдя 5 дюймов. Ее маршрут на развертке стакана показан на рис. 107. Именно так распространялся бы свет из точки, где сидела муха, в точку, где находится капля меда (от верхнего края стакана луч света отражается по закону: угол падения равен углу отражения). Из чертежа видно, что путь мухи равен длине гипотенузы прямоугольного треугольника с катетами в 3 и 4 дюйма.

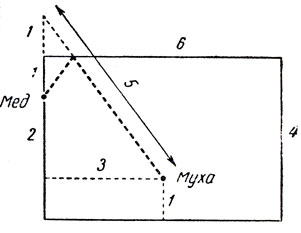
Рис. 107. Ответ к задаче о мухе и капле меда

Две дроби, сумма кубов которых равна 6, выражаются числами 17/21 и 37/21.

Ответ к задаче о пауках и мухе дан в книге Крайчика.