Глава 11. Девять новых задач

1. Соприкасающиеся сигареты. Четыре шара можно расположить так, что каждый из них будет касаться трех других. Пять монет можно установить так, что каждая монета будет касаться четырех остальных (рис. 47).

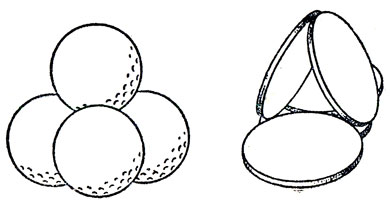
Рис. 47

Можно ли расположить шесть сигарет таким образом, чтобы каждая из них соприкасалась с пятью остальными?

2. Два парома. Два парома отходят одновременно от противоположных берегов реки и пересекают ее перпендикулярно берегам. Скорости у паромов постоянны, но у одного больше, чем у другого. Паромы встречаются друг с другом на расстоянии 720 м от ближайшего берега. Прежде чем плыть обратно, оба парома в течение 10 мин стоят у берега. На обратном пути они встречаются в 400 м от другого берега. Какова ширина реки?

3. Как найти длину гипотенузы? Прямоугольный треугольник вписан в четверть окружности так, как показано на рис. 48. Можете ли вы, пользуясь лишь теми данными, которые приведены на чертеже, вычислить длину гипотенузы АС?

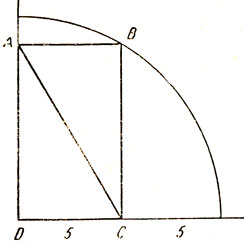
Рис. 48

На размышление дается одна минута!

4. Хитрый электрик. Однажды электрику пришлось столкнуться с довольно неприятной задачей.

В трехэтажном доме проведена скрытая проводка. Наружу провода выходят только в двух местах: на третьем этаже и в подвале. В том и другом случаях вывод представляет собой пучок из 11 абсолютно одинаковых проводов. Какой конец провода в верхнем выводе соответствует тому или иному концу провода в нижнем выводе, неизвестно. Именно это и должен был установить монтер.

Чтобы выполнить свою задачу, он может сделать две вещи:

1. закоротить любые провода вверху или внизу, скрутив их концы;
2. отыскать замкнутый контур с помощью специального тестера, состоящего из батарейки и звонка. Если такой прибор присоединить к концам неповрежденного провода, раздастся звонок.

Не желая понапрасну бегать вверх и вниз по лестнице, электрик, увлекавшийся к тому же. исследованием операций, уселся на ступеньке с карандашом и бумагой и вскоре придумал наиболее эффективный способ решения задачи.

В чем состоял его метод?

5. Как пересечь сеть прямых? Одна из самых старых топологических головоломок, известных любому школьнику, состоит в вычерчивании непрерывной линии, пересекающей по одному разу все 16 звеньев замкнутой сети прямолинейных отрезков, изображенных на рис. 49. Кривая, проведенная на этом рисунке, не может служить решением головоломки, потому что не пересекает одного звена сети. При построении решения использовать какие-нибудь трюки - проводить кривую через вершины сети, вдоль ее звеньев, складывать лист бумаги и т. д.- нельзя.

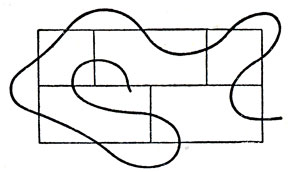
Рис. 49

Нетрудно доказать, что > на плоскости эта головоломка решения не имеет. Возникают два вопроса: можно ли решить ее на сфере? Существует ли решение на поверхности тора (бублика)?

6. Двенадцать спичек. Если считать, что спичка служит эталоном длины (ее длина принята за единицу длины), то 12 спичек можно различными способами расположить ка плоскости так, чтобы получились много угольники с целочисленной площадью. Два таких много угольника изображены на рис. 50: площадь квадрата равна 9, площадь креста - 5.

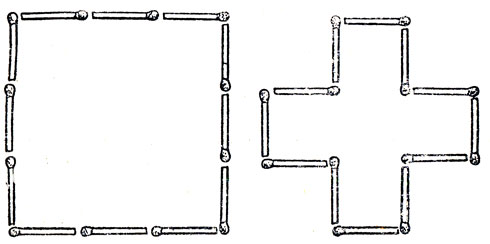
Рис. 50

Задача. Пользуясь всеми 12 спичками (длина каждой спички должна быть использована полностью), выложите периметр многоугольника, площадь которого равна 4.

7. Отверстие в шаре. На первый взгляд это совершенно невероятная задача (невероятная потому, что кажется, будто данных для решения недостаточно).

Через центр шара просверлено цилиндрическое отверстие длиной 6 см. Каков объем оставшейся части шара?

8. Влюбленные жуки. Четыре жука - А, В, С, D - сидят по углам квадрата со стороной 10 см (рис. 51). Жуки А и С - самцы, В и D - самки. Они начинают одновременно ползти: А к В, В к С, С к D и D к А. Если все жуки ползут с одинаковой постоянной скоростью, то они опишут четыре одинаковые логарифмические спирали, которые пересекаются в центре квадрата. Какое расстояние проползет до встречи каждый жук? Задача решается без вычислений.

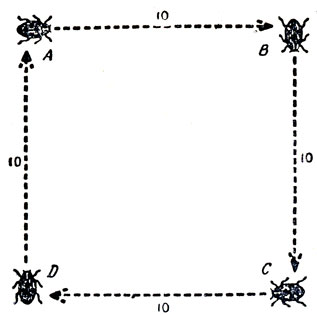
Рис. 51

9. Сколько детей?- Я слышу, в саду играют дети,- сказал Джон.- Неужели все они ваши?

- Боже упаси, конечно, нет,- воскликнул профессор Смит, известный специалист по теории чисел.- Там, кроме моих детей, играют еще и дети троих соседей, но наша семья самая большая. У Браунов детей меньше, чем у меня, у Гринов - еще меньше, а меньше всего детей у Блэков".

- А сколько всего детей?- спросил Джон.

- На этот вопрос я отвечу так,- сказал Смит.- Детей меньше восемнадцати, а если перемножить между собой число детей в семьях, то получится номер моего дома, который вы видели, когда пришли.

Джон достал из кармана блокнот и карандаш и принялся за вычисления. Через некоторое время он поднял голову и сказал: "Нужна еще кое-какая информация. У Блэков больше одного ребенка?"

Как только Смит ответил, Джон улыбнулся и правильно назвал число детей в каждой семье.

Джону задача показалась тривиальной, поскольку он знал номер дома, а профессор сообщил ему, сколько детей у Блэков - один или больше. Но оказывается, что число детей в каждой семье можно определить и без этой дополнительной информации!

1. Существует несколько различных способов размещения сигарет. На рис. 52 показано традиционное решение, которое обычно приводится в старых сборниках головоломок.

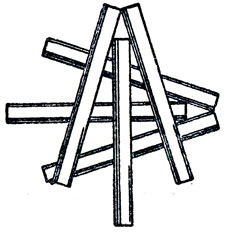
Рис. 52

К моему удивлению, около пятнадцати читателей обнаружили, что семь сигарет тоже можно разложить так, чтобы каждая касалась всех остальных! Из-за этого первую задачу следует считать устаревшей. На рис. 53, который прислали Дж. Рибики и Дж. Рейнольде, показано, как это делается. Схема нарисована для критического случая, когда отношение длины сигареты к ее диаметру равно ⁷/₂ √3. Тогда точки касания расположены точно на концах сигарет. Это решение годится также для любого отношения длины к диаметру, большего чем ⁷/₂ √3. Если изучить размеры существующих сигарет, то получится отношение около 8 к 1, то есть число, большее чем ⁷/₂ √3, поэтому наше решение останется в силе. Обратите внимание, что если убрать центральную сигарету, которая на рисунке обращена прямо на читателя, то шесть оставшихся дадут очень симметричное решение первоначальной задачи.

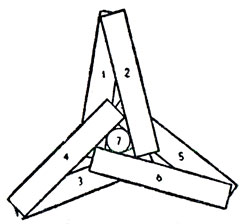
Рис. 53

2. Когда паромы встречаются первый раз (верхняя часть рис. 54), сумма пройденных ими расстояний равна ширине реки. Когда каждый из них причаливает к противоположному берегу, эта сумма равна удвоенной ширине реки, а когда они встречаются второй раз (нижняя часть рис. 54), сумма пройденных ими расстояний в три раза больше ширины реки. Поскольку оба парома двигаются с постоянной скоростью в течение одного и того же промежутка времени, мы можем заключить, что к моменту второй встречи каждый из них прошел расстояние втрое больше пройденного к моменту первой встречи. Это расстояние равно ширине реки. Поскольку белый паром прошел до первой встречи 720 м, к моменту второй встречи все пройденное им расстояние равно 720×3 = 2160 м. Из чертежа видно, что это расстояние на 400 м больше ширины реки, поэтому надо из 2160 вычесть 400. Получится 1760 м. Это и есть ширина реки. Время стоянки паромов в решение не входит.

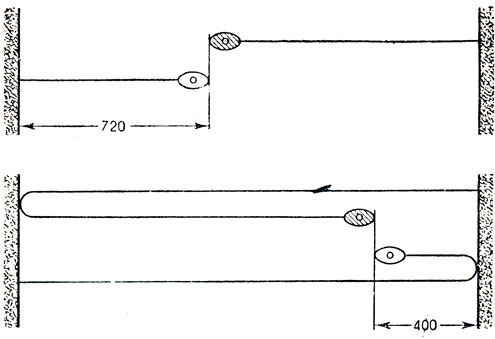
Рис. 54

К решению задачи можно подойти и иначе. Пусть ширина реки х. Вначале отношение расстояний, пройденных паромами, равно (х - 720)/720. Ко второй встрече оно будет составлять (2х - 400)/(х + 400). Эти отношения равны, из них мы легко находим х.

3. Линия АС является одной из диагоналей прямоугольника ABCD (рис. 55). Вторая диагональ BD служит радиусом окружности, длина которого равна 10 единицам. Поскольку диагонали равны, длина линии АС также равна 10 единицам.

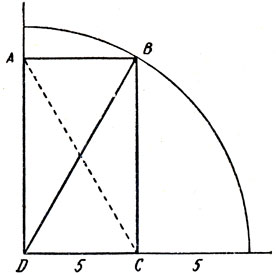
Рис. 55

4. Электрик закоротил на верхнем этаже пять пар проводов (закороченные попарно провода соединены пунктирными линиями на рис. 56), оставив один провод свободным. Потом он спустился вниз и с помощью тестера нашел нижние концы закороченных пар. На рисунке показано, какими буквами он обозначил провода. Затем он закоротил те провода, которые соединены пунктиром внизу. пунктиром внизу.

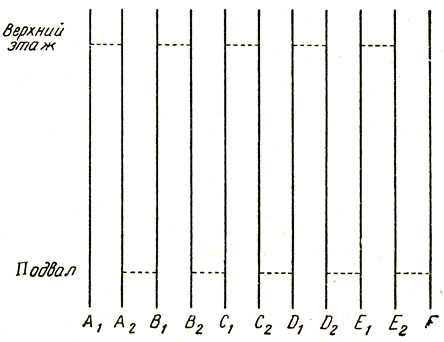
Рис. 56

Вернувшись наверх, он разъединил закороченные провода, но оставил их скрученными попарно. Затем он подсоединил тестер к свободному проводу (он знал, что это верхний конец провода F) и к одному из остальных. Определив второй провод, он смог установить, что это E₂, а соседний провод - E₁. Затем он подключил прибор к E₁ и к проводу, который оказался D₂. Это позволило электрику установить, что соседний конец принадлежит проводу D₁. Следуя своему методу, он легко нашел все провода. Указанный способ годится для любого нечетного числа проводов.

Немного изменив этот метод, можно применить его к любому четному числу проводов больше двух. Предположим, что справа на рис. 56 есть двенадцатый провод. Наверху закорачиваются те же пять пар проводов, а два остаются свободными. Внизу провода закорачиваются, как прежде, а двенадцатый провод обозначается буквой G. Вернувшись наверх, электрик легко находит G: это единственный из двух свободных проводов, который ни с каким другим не связан. Остальные одиннадцать проводов распознаются так же, как раньше.

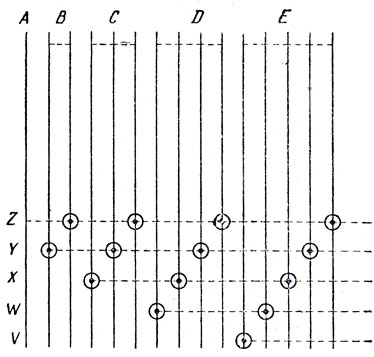
Рис. 57

Существует в каком-то смысле более рациональный метод, применимый к любому числу проводов, кроме двух (задача о двух проводах не имеет решения). Этот метод легко объяснить на схеме из четырнадцати проводов (рис. 57). Метод заключается в следующем:

1. Верхний этаж. Закоротите провода по одному, два, три и т. д. Обозначьте закороченные группы буквами А, В, С, D и т. д. Последняя группа может быть неполной.
2. Нижний этаж. Установите выделенные ранее группы проводов с помощью тестера. Пронумеруйте провода и объедините их в новые группы Z, Y, X, W, V, ...
3. Верхний этаж. Разъедините провода. Теперь их номера можно определить с помощью тестера. Провод 1 - это, конечно, А. Провод 3 - это единственный провод в группе В, соединенный с 1. Его соседом должен быть 2. В группе С только провод 6 соединяется с 7. С 2 соединяется только 5. Провод, остающийся в С, будет 4. И так далее для других групп.

Чертеж можно неограниченно продолжать вправо. Для случая n проводов чертеж следует оборвать на n-м проводе.

5. Непрерывная линия, которая входит в каждый прямоугольник и выходит из него, обязательно пересекает два отрезка. На рис. 58 каждая из областей A, В и С ограничена нечетным числом отрезков. Следовательно, если линия пересекает все отрезки, то концы ее должны лежать внутри прямоугольников A, В и С. Но у непрерывной кривой только два конца, поэтому на плоскости задача неразрешима.

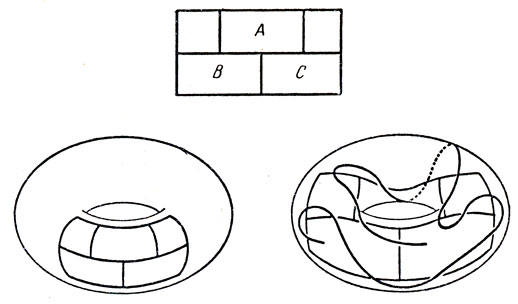
Рис. 58

Те же рассуждения применимы, если сетка нарисована на сфере или на торе (левый нижний рисунок). Однако на торе сетку можно нарисовать так (правый нижний рисунок), что отверстие тора будет внутри одного из трех прямоугольников А, В или С, и тогда задача решается легко.

6. Из двенадцати спичек можно построить прямоугольный треугольник со сторонами в три, четыре и пять единиц, как показано на рис. 59 слева. Его площадь равна шести квадратным единицам. Изменив положение трех спичек так, как показано на правом рисунке, мы уменьшим площадь фигуры на две квадратные единицы.

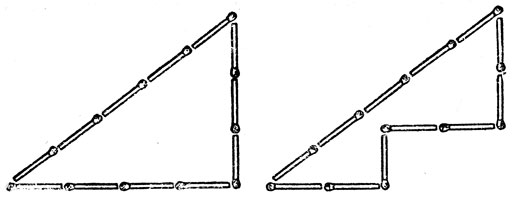
Рис. 59

Получится многоугольник с площадью, равной четырем квадратным единицам.

Это решение приводится во многих сборниках головоломок. Имеются и сотни других решений. Существует связь между этой задачей и игрой в полиомино, о которой рассказывается в следующей главе. Каждая из пяти фигур тетрамино (состоящих из четырех единичных квадратов каждая) позволяет найти много решений задачи со спичками. Нужно лишь отбрасывать квадраты, заменяя их равновеликими по площади треугольниками до тех пор, пока длина периметра получившейся фигуры не достигнет 12 спичек. Некоторые из таких фигур показаны на рис. 60. В каждом стоят фигурки, построенные из одного и того же элемента тетрамино.

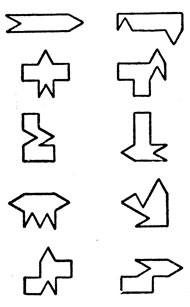
Рис. 60

Возможно решение в виде звезды (рис. 61). Подбирая ширину лучей, можно получать звезду любой площади от 0 до 11,196 квадратных единиц - площади правильного десятиугольника, наибольшей площади, которую можно ограничить периметром длиной в 12 спичек.

Рис. 61

7. Задачу об объеме оставшейся части шара можно решить, не прибегая к высшей математике. Пусть R - радиус шара. Как видно из рис. 62, радиус цилиндрического отверстия равен √(R²-9), а высота сферических шапочек на концах цилиндра равна R - 3. Для вычисления объема остатка, получающегося после того, как вырезаны цилиндр и шапочки, нужно прибавить объем цилиндра 6π(R²-9) к удвоенному объему сферической шапочки и вычесть эту сумму из объема шара (4π/3)R³, Объем шапочки вычисляется по формуле πA(3r² + A²)/6, где A - высота, а r - радиус.

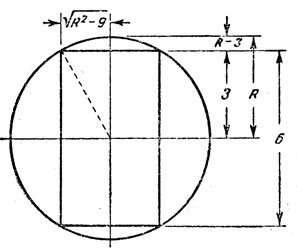
Рис. 62

При вычислении все члены взаимно уничтожаются, кроме 36π. Это число и равно объему остатка в кубических единицах. Другими словами, объем остатка постоянен, независимо от размера сферы и диаметра отверстия.

Самое раннее упоминание об этой задаче я нашел у С. Джонса^*. Там же приводится и аналогичная двумерная задача. Если в кольце произвольного размера провести самую длинную прямую линию, то площадь кольца равна площади круга, построенного на этой прямой как на диаметре (рис. 63).

^* (S. I. Jones, Mathematical Nuts, 1932, pp. 86, 93.)

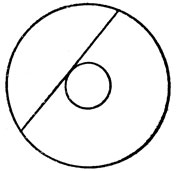
Рис. 63

Некоторые читатели быстро решили задачу с помощью весьма тонкого рассуждения. Редакция не стала бы предлагать задачу своим читателям, если бы та не имела единственного решения. Но коль скоро задача имеет единственное решение, объем оставшейся части шара не зависит от радиуса отверстия и сохраняет свое постоянное значение даже тогда, когда радиус отверстия становится равным нулю. Поэтому объем оставшейся части шара равен объему шара диаметром 6 см, то есть 36π см³.

8. В любой момент времени жуки находятся в вершинах квадрата, который сжимается и поворачивается по мере сближения жуков. Поэтому путь преследователя всегда будет перпендикулярен пути преследуемого. Это значит, что если А приближается к В, то скорость В не имеет компоненты вдоль направления скорости А. Следовательно, А поймает В через такой же промежуток времени, как если бы В стоял на месте. Длина каждой спирали будет равна стороне квадрата - 10 см.

Если же три жука выползают из вершин равностороннего треугольника, то составляющая скорости каждого жука, направленная к его преследователю, будет равна половине всей скорости жука (косинус угла 60° есть ¹/₂). Поэтому жуки будут сближаться со скоростью ³/₂, если за единицу принять скорость жука относительно бумаги. Жуки встретятся в центре треугольника через промежуток времени, равный отношению стороны треугольника к утроенной скорости жука. Каждый жук при этом проползет расстояние, равное ²/₃ стороны треугольника.

9. Когда Джон задумался над задачей профессора, ему было известно, что во всех семьях количество детей различно, а всего детей меньше 18. Кроме того, он знал, что если перемножить число детей, то получится номер дома профессора. Поэтому прежде всего он должен был разложить номер дома на множители, сумма которых была бы меньше 18. Если бы это можно было сделать только одним способом, то Джон решил бы задачу сразу. Поскольку он не мог ее решить без дополнительной информации, мы делаем вывод, что номер дома допускает разложение на множители более чем одним способом. Придя к такому заключению, мы должны выписать все возможные комбинации четырех различных чисел, сумма которых не превышает 18, и вычислить произведения каждой четверки. Оказывается, что во многих случаях одно и то же произведение получается для разных комбинаций чисел. Как же решить, какое из произведений равно номеру дома?

Ключ к решению заключается в вопросе Джона о том, имеет ли самая маленькая семья больше одного ребенка. Этот вопрос приобретает смысл лишь в том случае, если номер дома 120. Разложить это число на множители можно следующими способами: 1×3×5×8, 1×4×5×6 и 2×3×4×5. Если бы Смит ответил отрицательно, задача оставалась бы нерешенной. Но раз Джон ее все-таки решил, это значит, что ответ был положительным. Поэтому в семьях было 2, 3, 4 и 5 детей.