
Математические модели самовоспроизведения. Эдвард Ф. Мур. Лаборатории компании "Белл телефон", Марри-Хилл, Нью-Джерси
Введение. Способность к самовоспроизведению долгое время рассматривалась как одно из наиболее характерных свойств, присущих живым организмам. Фон Нейман был первым ученым, детально рассмотревшим задачу о том, при каких условиях способны к самовоспроизведению машины, рассчитывая, что решение этой задачи прольет свет как на фундаментальные проблемы биологии, так и на проблему (интерес к которой стимулируется также и небиологическими науками), касающуюся потенциальных возможностей автоматов и пределов их возможностей. В течение ряда лет фон Нейман читал отдельные лекции и серии лекций, посвященные общей и логической теории автоматов, в которых он отчасти касался вопроса о самовоспроизводящихся машинах. В работе [17] содержится одна из его ранних лекций по этому вопросу; в некоторых из более поздних лекций как содержание, так и подход к проблеме уже иные. Я слушал только один из более поздних курсов лекций, но по литературе и пересказам слушателей я ознакомился также и с идеями, изложенными в других лекциях. Сначала фон Нейман изучил кинематическую модель самовоспроизведения, в которой рассматриваются трехмерные физические объекты, являющиеся теми частями, из которых самовоспроизводящаяся машина должна быть собрана. Предполагается, что машина помещена в резервуар, в котором вокруг нее плавают неограниченные запасы этих частей (наподобие частиц пищи в питательной среде), и машина, находя необходимые ей части и собирая их, изготовляет свою копию.
В своих более поздних лекциях фон Нейман сконструировал более абстрактную модель, отличающуюся от кинематической и менее похожую на реальный мир. Он рассмотрел вселенную в виде двумерного евклидова пространства, разбитого на квадратные ячейки равного размера, наподобие клетчатой бумаги или шахматной доски. Я буду называть такое пространство сотообразным (клеточным), но буду понимать этот термин, в несколько специальном смысле. В каждой ячейке этих сотов должна быть расположена одна копия некоторого конечного автомата (т. е. автомата с конечным числом состояний). Каждая клетка-автомат должна быть детерминированной и синхронизированной, т. е. в каждый целочисленный момент времени T>0 состояние каждой клетки-автомата зависит только от ее собственного состояния в момент времени Т-1 и от состояния в этот момент соседних с ней клеток-автоматов. Все клетки-автоматы должны иметь совершенно одинаковый набор состояний, в которых они могут находиться, и одинаковые правила перехода из одного состояния в другое, но различные клетки-автоматы могут находиться в различных состояниях. Набор возможных состояний клеток-автоматов обязательно должен включать в себя специальное состояние, называемое состоянием покоя, и в этом состоянии должны быть все клетки-автоматы, за исключением конечного числа. Состояние покоя должно обладать следующим свойством: если какая-либо клетка-автомат и все ее соседи в момент времени Т-1 находятся в состоянии покоя, то и в момент времени Т рассматриваемая клетка-автомат должна быть в состоянии покоя.
Всю систему в совокупности, т. е. систему, состоящую из рассматриваемого сотообразного (клеточного) пространства, набора возможных состояний, правил перехода из одного состояния в другое и т. д., будем называть сотообразной структурой. Эта сотообразная структура отличается от сотообразного (клеточного) пространства примерно так же, как группа (включая операцию умножения, определенную для элементов группы, и правило нахождения обратного элемента) отличается от множества элементов группы.
Часть сотообразного пространства, занимаемую конечным числом ячеек, будем называть блоком. Конфигурация, или состояние такого блока, есть функция, которая ставит в соответствие каждой ячейке определенное состояние, т. е. конфигурация блока определяет, какое состояние каждая клетка блока имеет в данный момент времени Т. Пример такой конфигурации дан на рис. 1, где блок содержит семь ячеек, а состояние каждой клетки-автомата указано символом, написанным в соответствующей ячейке.
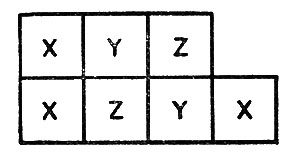
Рис. 1. Пример части сотообразного пространства, демонстрирующий конфигурацию, определенную только для семи ячеек
Фон Нейман рассматривал задачу нахождения такой сотообразной структуры, у которой клетки-автоматы имеют лишь небольшое число состояний и образуют конфигурации, обладающие свойством самовоспроизведения. Детали создания такой структуры, возможно, отчасти напоминали бы составление программы для цифровой вычислительной машины, и при этом удалось бы избежать трудностей, связанных с проблемами движения, сборки и геометрии, возникающими в кинематической модели. Фон Нейман решил большую часть вопросов, относящихся к задаче о том, как можно сконструировать самовоспроизводящуюся машину в рамках как кинематической, так и сотообразной модели. Несмотря на то что он не успел закончить эту работу, предполагается, что она будет опубликована (см. [16]).
Кинематические модели самовоспроизведения. Ранние работы по вопросам самовоспроизведения выполнены фон Нейманом в рамках кинематической модели, в которой для сборки частей требуется движение, а позже он обратился к сотообразной модели, которая хотя и представляется менее живой, яркой и реалистичной, но зато легче для математической обработки. Однако недавно удалось построить и продемонстрировать довольно интересные кинематические модели.
Один из способов осуществить необходимое пространственное движение при помощи просто контролируемых электрических средств -это использовать модель железной дороги. Маневрирование поездов при помощи электрических устройств сейчас уже легко осуществимо и не требует проектирования и разработки новых средств. При этом перестройка порядка подаваемых частей может быть осуществлена переводом вагонов на разъездные пути. Необходимый логический контроль и программирование могут быть осуществлены при помощи релейных цепей, вмонтированных в отдельные вагоны. Таким образом, в этом случае самовоспроизводящаяся машина представляет собой поезд, составленный из разных типов вагонов, каждый из которых рассматривается как элементарная составная часть или сырье. Джекобсон сконструировал действующую модель самовоспроизведения, состоящую из железнодорожных путей и вагонов [6]. Он описал несколько типов таких моделей разной степени общности и осуществил постройку простейшего из предложенных им вариантов. В определенном смысле реализованная модель довольно тривиальна, и в отношении способности к самовоспроизведению она наименее общая из описанных Джекобсоном моделей.
Другие кинематические модели, несколько более общие и менее тривиальные, чем модель Джекобсона, и основанные на совершенно других принципах, чем железнодорожная модель, были предложены Пенроузом. Простейшую из них (она приведена на рис. 1 в статьях [19, 20] или на рис. 2 в статье [21]) назовем основной моделью Пенроуза, ибо другие модели, хотя и похожи на нее, но в определенном отношении отличаются от нее и обладают характерными особенностями.
В основной модели Пенроуза используется только два типа элементов: А и В. Каждый из элементов представляет собой сплошной жесткий кусок твердого материала, вырезанного в форме определенных крюков и захватов так, что два элемента могут сцепиться друг с другом двумя различными способами, образуя либо машину АВ, либо машину ВА. Если некоторое число несцепленных элементов поместить в "случайном порядке" в прямоугольный ящик подходящего размера, где уже находится машина АВ, и после этого регулярно встряхивать ящик, то за счет механических сил, сил сцепления и силы тяжести образуется много ее копий, причем в этом случае совершенно не используются электрические и магнитные силы или химические реакции. Если встряхивание несцепленных элементов производить в присутствии машины ВА, то будут получаться копии этой машины. Следовательно, вполне резонно назвать машины АВ и ВА зародышами. Если же встряхивать не-сцепленные элементы, среди которых нет зародыша, то не произойдет никакого "самопроизвольного зарождения" и не образуется никаких зародышей; но если встряхивать ящик каким-нибудь необычным способом, то "самопроизвольное зарождение" может произойти.
В этой статье умышленно не приведено изображение элементов основной модели Пенроуза, ибо если читатель сам попробует найти форму, обеспечивающую названные свойства элементов А и В, то трудности, которые он при этом встретит, помогут ему по достоинству оценить остроумие простого решения, найденного Пенроузом.
После того как я сделал точную копию основной модели Пенроуза, я обнаружил, что она не только весьма удовлетворительно работает, но и очень полезна для того, чтобы демонстрировать аудитории проблемы и возможности самовоспроизводящихся машин.
Существует одно недоразумение относительно биологической интерпретации основной модели Пенроуза, которое хотелось бы разъяснить. Когда такую модель демонстрируют инженерам, математикам или физикам, многие из них предполагают, что два типа элементов соответствуют мужскому и женскому индивидуумам. Но это совершенно неуместная аналогия. Одна из машин АВ или ВА соответствует индивидууму, а элементы соответствуют различным молекулам химических соединений, из которых состоят хромосомы. Дело в том, что наличие именно двух типов элементов может дезориентировать людей, позабывших биологию. В случае модели Пенроуза осуществляется бесполовое воспроизведение, индивидуум состоит только из одной хромосомы, а хромосома- из двух молекул. Более общие и менее тривиальные примеры самовоспроизводящихся машин должны были бы иметь вид длинной цепочки, состоящей из многих элементов, наподобие реальной хромосомы. И действительно, Пенроуз в своей статье описал такие более общие модели. Однако модели, еще более напоминающие живые прототипы, т. е. модели, которые обладали бы несколькими хромосомами и имели бы также дополнительные элементы, образующие структуры, аналогичные цитоплазме и мембране клетки, до сих пор еще не были детально описаны в печати.
Другие кинематические модели самовоспроизведения (использующие электромагниты и электреты, плавающие в жидкости) были предложены Моровицем {12], но, очевидно, эти модели не были ни детально разработаны, ни построены, так что еще неизвестно, насколько хорошо будут работать такие машины.
Сотообразные модели самовоспроизведения. До того как будут более детально определены и описаны сотообразные структуры, следует предупредить читателя, что в этом случае машинами (автоматами) можно назвать три различные вещи. Соты (т. е. совокупность клеток) сами по себе можно считать машиной, хотя в сотообразной модели самовоспроизведения соты (т. е. совокупность ячеек) более естественно рассматривать как окружающую среду или вселенную (осуществляющую снабжение частями или сырьем), в которой происходит самовоспроизведение. Конфигурацию (представляющую собой состояние блока конечного размера) можно рассматривать как машину; она действительно является машиной, способной, как это можно показать, воспроизводить саму себя. Можно также считать машиной ячейку, ибо последняя обладает набором состояний и правилами перехода из одного состояния в другое, но в сотообразной модели самовоспроизведения она соответствует одной из элементарных компонент, из которых построена машина. Ввиду того, что каждую из этих трех вещей можно назвать автоматом, следует проявить осторожность и не допустить никакого смешения между этими тремя типами автоматов. Пример ошибки, которая произошла именно по этой причине, содержит статья Розена [25], где утверждается, что допущение существования самовоспроизводящегося автомата приводит к парадоксу. Возникновение этого мнимого парадокса лучше всего можно объяснить тем, что Розен не обратил внимания на различие между сотами и конфигурацией, хотя на самом деле он даже и не использовал этих слов.
Для N-мерного евклидова пространства (N - любое целое положительное число) можно определить соты так же, как в случае N = 2; построения и результаты очень сходны. На самом деле реальный биологический интерес представляет собой случай N = 3. В своих лекциях (Принстонский университет, 2-5 марта 1955 г.) фон Нейман сказал, что сначала он думал, что придется использовать трехмерную модель, так как коммутационная схема самовоспроизводящейся машины могла оказаться не плоской. Но потом ему удалось придумать метод связи посредством передачи через соседей; этот метод был использован в автоматах, названных мною двумерными сотообразными структурами. Работать с двумерным пространством наверняка легче, ибо картинки, изображающие конфигурации, можно рисовать на бумаге. Шеннон указал мне (в неопубликованном частном сообщении) схему самовоспроизведения, которую можно выполнить даже в виде одномерной сотообразной структуры, но все же кажется, что двумерная модель гораздо интереснее. За исключением специально оговоренных случаев, в этой статье мы будем иметь дело с сотами, полученными при разбиении на клетки двумерного евклидова пространства.
Формально сотообразную структуру следует определить как пятерку (N, T, S, q0, f), где N - целое положительное число, T (сами соты) - разбиение N-мерного евклидова пространства на ячейки, представляющие собой N-мерные единичные кубы с целочисленными координатами центра, S - конечное множество, элементы которого называются состояниями, q0 - особый элемент множества S, называемый состоянием покоя, и f - функция, которая отображает множество состояний ячейки и ее соседей в момент T-1 (всего 3N состояний) в состояние ячейки в момент T. Однако в рамках этой статьи не обязательно формальное (и из-за этого сложное) изложение, и мы ограничимся лишь этим кратким замечанием.
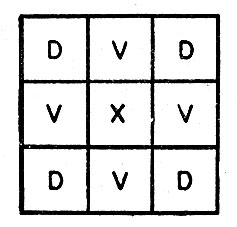
Рис. 2. Девять ячеек, являющихся соседями ячейки X
В дальнейшем соседями данной ячейки мы будем считать все те ячейки (включая в число соседей и саму ячейку), у которых каждая координата либо совпадает с координатой данной ячейки, либо отличается от нее не более чем на единицу. На рис. 2 все девять ячеек являются соседями ячейки X. Это определение приводит к тому, что все соседи ячеек прямоугольного блока (т. е. ячеек, покрывающих площадь прямоугольника) имеют в свою очередь вид прямоугольника, и, следовательно, легче подсчитать число ячеек в данном блоке. На самом деле указанное здесь точное определение соседей не так уж важно. Фон Нейман рассматривал лишь пять ячеек (обозначенных на рис. 2 буквами V и X) и считал, что состояние ячейки X в момент Т зависит от состояния в момент Т-1 этих пяти ячеек (см. работу [16]).
Однако его определение соседей является частным случаем моего, так как я просто могу так задать функцию, определяющую состояние ячейки, что состояние ячейки X в момент Т не будет зависеть от состояния в момент Т-1 ячеек, обозначенных на рис. 2 буквой D.
Функция f, которая определяет состояние каждой ячейки (для всех моментов времени T>0) в зависимости от состояния ее соседей в предыдущий момент времени, одинакова для всех ячеек на плоскости. Это по существу требование однородности, гласящее, что физические законы должны быть одинаковы во всех местах вселенной. Кроме того, мы требуем, чтобы функция f была такой, чтобы ячейка, все соседи которой в момент времени Т-1 находились в состоянии покоя, сама перешла бы в это состояние в момент Т. На рис. 3 состояние покоя обозначено нулем.

Рис. 3. Эта конфигурация содержит три (а не четыре) копии конфигурации, изображенной на рис. 1
Для того чтобы можно было определить состояние всех ячеек, мы потребуем, чтобы в момент T = 0 все ячейки, за исключением лишь конечного числа их, были в состоянии покоя. Отсюда будет следовать, что в каждый момент времени T>0 все ячейки, за исключением лишь конечного числа их, будут находиться в состоянии покоя, хотя и возможно, что число ячеек, находящихся в активном состоянии (т. е. отличном от состояния покоя), будет расти со временем.
Будем говорить, что конфигурация с является копией конфигурации с', если существует перенос плоскости, переводящий блок с в блок с' так, что каждая ячейка блока с имеет то же состояние, что и соответствующая ей ячейка в блоке с'.
Будем говорить, что конфигурация с* содержит n копий конфигурации с, если у блока с* существует n непересекающихся подмножеств, каждое из которых является копией блока с. Это определение иллюстрируется на рис. 3, где показана конфигурация, содержащая три копии конфигурации, изображенной на рис. 1. Если же слово "непересекающихся" заменить словом "различных", то конфигурация, изображенная на рис.3, содержала бы четыре такие копии.
Будем говорить, что конфигурация с способна произвести n потомков за время T, если, приняв копию конфигурации с за исходную (исходная - это та конфигурация, которой в момент T = 0 обладает множество всех ячеек, находящихся в активном состоянии), можно указать такое время Т'<Т, что в конфигурации, которой обладает множество всех ячеек, находящихся в момент Т' в активном состоянии, будет содержаться по крайней мере n копий конфигурации с.
Будем говорить, что конфигурация самовоспроизводящаяся, если для каждого целого положительного n существует такое T, что она способна воспроизвести n потомков за время Т. Это определение не исключает тривиальных примеров самовоспроизводящихся конфигураций. Рассмотрим сотообразую структуру, у которой существует только два состояния X и 0 и которая обладает таким правилом перехода между этими состояниями, что любая ячейка, имеющая в момент Т-1 соседа в состоянии X, в момент Т сама перейдет в состояние X. Тогда конфигурация, состоящая из одной ячейки в состоянии X, будет самовоспроизводящейся. Это ближе к модели роста кристаллов, чем к самовоспроизведению.
Чтобы получить самовоспроизводящуюся конфигурацию, которую наверняка можно рассматривать как нетривиальную, фон Нейман потребовал, чтобы каждая конфигурация содержала универсальную машину Тьюринга. Можно было бы думать, что наиболее легкий способ избежать тривиальности - это суметь указать такую самовоспроизводящуюся конфигурацию, которая бы содержала копию любой заданной конфигурации, но теорема 2 показывает, что это невозможно.
Обычно полагают, что при самовоспроизведении живых организмов происходит экспоненциальный рост популяции со временем; например размер популяции может удваиваться с каждым новым поколением. Этого не может быть в сотообразной вселенной, на что указывает следующая теорема.
Теорема 1. Если самовоспроизводящаяся конфигурация способна воспроизвести f(T) потомков за время Т, то существует такое действительное положительное число k, что f(T)≤kT2.
Доказательство. Пусть с - самовоспроизводящаяся конфигурация, и пусть наименьший квадратный блок, который может вместить конфигурацию, являющуюся копией конфигурации с, имеет размер D×D. Тогда в каждый момент времени Т общее число ячеек в активном состоянии не будет превышать (2T + D)2. Если r - число ячеек в этом блоке, то

откуда и следует заключение теоремы.
Мальтузианские рассуждения о том, что число потомков не может расти быстрее квадрата времени, ибо иначе для потомков не хватило бы места, основаны в действительности на том факте, что скорость распространения активного состояния по среде ячеек, находящихся в состоянии покоя, конечна, так как за единицу времени район, занимаемый ячейками в активном состоянии, растет только на одну ячейку в каждом направлении. В общих чертах это соответствует такому физическому ограничению, как конечная скорость света.
Кроме того, наше рассуждение зависит также и от размерности пространства, ибо для N-мерной сотообразной структуры соответствующей мажорантой была бы величина kTN.
Несколько раз до этого мы уже упоминали об особой природе момента T = 0. Пусть ячейки сотообразной структуры подчиняются правилам перехода для всех моментов времени T>0, а для момента Т = 0 мы произвольно определим начальное состояние. Для того чтобы проверить, является ли данная конфигурация самовоспроизводящейся, мы (в начальный момент времени) поместим в соты ее копию и окружим последнюю ячейками, находящимися в состоянии покоя. Это единственный момент времени, когда можно по своему усмотрению поместить в сотах любую конфигурацию.
Оказывается, при некоторых разумных предположениях относительно сотообразной структуры, всегда будет конфигурация, которая может существовать только в момент T = 0. Иными словами, эта конфигурация не только нестабильна, но она и неконструируема в том смысле, что не существует такой конфигурации, задав которую в момент времени Т- 1, можно было бы из нее получить данную нестабильную конфигурацию в момент Т с помощью функции f, определяющей правила перехода. Эту неконструируемую конфигурацию мы будем называть конфигурацией райского сада (сада Эдема). Этот термин, заимствованный из Библии, был предложен Джоном В. Текеем.
Так как конфигурация райского сада не может быть получена ни из какой другой конфигурации, то никакая самовоспроизводящаяся конфигурация не может содержать копию конфигурации райского сада. Поэтому исследование условий, при которых такие конфигурации могут встретиться, прольет свет на пределы возможностей автоматов воспроизводить самих себя.
Условия, при которых могут встретиться конфигурации райского сада, связаны со способностью осуществлять стирание. После того как с доски стерт мел, невозможно ничего сказать о том, что раньше было на ней написано; по аналогии с этим термин "стирание" используется конструкторами вычислительных машин по отношению к ячейкам памяти машины. Стирание представляет собой необратимый процесс, переводящий конфигурацию в такое состояние, по которому невозможно определить ее предшествующее состояние.
Однако если мы имеем сотообразную структуру, для которой функция перехода f такова, что состояние каждой ячейки есть просто предыдущее состояние соседней с ней левой ячейки, то не хотелось бы считать, что здесь происходит стирание. Внутри фиксированного блока ячеек мы можем оказаться не в силах восстановить прошлое состояние ячеек, но информация о прошлом состоянии не уничтожена, а просто сдвинута вправо. Таким образом, при формальном определении стирания необходимо проявить осмотрительность и просмотреть ячейки, соседние с конфигурацией, чтобы быть уверенным, что информация не оказалась просто перенесенной от рассматриваемой конфигурации к соседним ячейкам. Кроме этого, необходимо определить, что произойдет с ячейками, соседними с соседями рассматриваемой конфигурации, чтобы быть уверенным, что и новая информация не сдвинулась от них вовне. Таким образом, формальное определение должно быть связано с рассмотрением ситуации в целом.
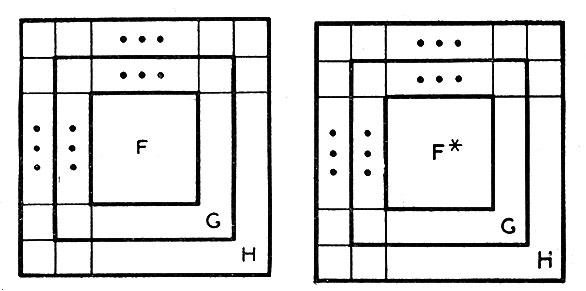
Рис. 4. Изображение конфигураций двух различных блоков одинакового размера, существующих в момент времени Т (время Т входит в определение стираемой конфигурации)
Рассмотрим показанную на рис. 4 пару конфигураций для двух блоков одинакового размера. Не ограничивая общности, будем считать оба эти блока квадратными. В обоих случаях рассмотрим внутренние блоки, конфигурации которых в момент Т обозначим соответственно через F и F*. Рассмотрим затем промежуточные блоки (в виде квадратов рамки), состоящие из множества всех ячеек, соседних с вышеупомянутыми внутренними блоками, за вычетом всех ячеек, принадлежащих самим внутренним блокам. Допустим, что в момент Т конфигурации обоих промежуточных блоков равны G, т. е. потребуем, чтобы эти конфигурации были копиями друг друга.
Далее рассмотрим аналогичным образом построенные внешние блоки и потребуем, чтобы в обоих случаях в момент Т они имели конфигурацию H, т. е. были копиями друг друга. Пусть F≠F*, т. е. пусть внутренние блоки в момент Т имеют разные конфигурации (но оба они в момент Т должны быть согласованы вдоль двух граничных слоев). Если мы имеем такую пару конфигураций, и если в момент T+1 (см. рис. 5) конфигурации внутренних блоков являются копиями друг друга, и если, наконец, конфигурации промежуточных блоков тоже будут копиями друг друга, то мы будем называть конфигурации такой пары взаимно стираемыми.
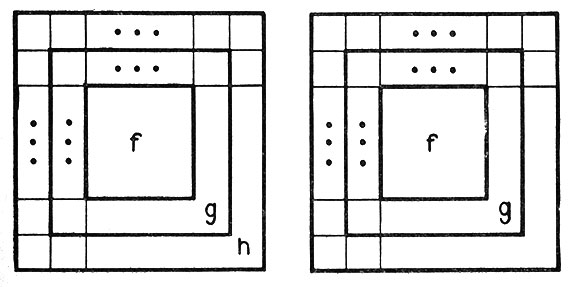
Рис. 5. Изображение конфигураций двух идентичных блоков, существующих в момент времени T+1 (время Т+1 входит в определение стираемой конфигурации)
(Заметим, что конфигурацию h внешнего блока, вообще говоря, нельзя даже определить, ибо состояние ячеек этого блока зависит от состояний ячеек, находящихся вне трех рассмотренных блоков.) Отношение взаимной стираемости транзитивно и симметрично, и, следовательно, конфигурации могут быть разбиты на классы эквивалентности, каждый из которых состоит либо из конфигураций, являющихся копиями друг друга, либо из взаимно стираемых конфигураций.
Назовем конфигурацию с стираемой, если существует другая конфигурация с', такая, что с и с' взаимно стираемы. В работе [11] стираемые конфигурации названы "конфигурациями, которые могут забывать", но термин "стираемая" не только менее антропоморфен, но и лучше соответствует терминологии, используемой инженерами-электротехниками.
Следует заметить, что если с- стираемая конфигурация, а c' - такая конфигурация прямоугольного блока, что в ней содержится копия конфигурации с, то и c' - стираемая конфигурация. Это позволяет нам считать, что стираемые конфигурации связаны с квадратными блоками.
Не все сотообразные структуры могут содержать стираемые конфигурации. Если функция f, определяющая правила перехода, и набор состояний ячеек таковы, что не может быть необратимого перехода, то существует лишь ограниченный класс методов построения конфигураций и их расчета.
Перейдем теперь к изложению основного результата этой статьи.
Теорема 2. В сотообразной структуре, в которой существуют стираемые конфигурации, существуют и конфигурации райского сада.
Сначала будет дана схема интуитивной идеи доказательства, а затем детально доказано неравенство, из которого следует утверждение теоремы. Пусть n - такое целое число, что существует блок размера n×n, содержащий стираемую конфигурацию. Для целого k (которое мы выберем в процессе доказательства) мы рассмотрим блок размера kn×kn, изображенный на рис. 6.
Каждый из k2 блоков размера n×n (см. рис. 6) достаточно велик, чтобы содержать копию стираемой конфигурации; k следует выбрать таким, чтобы в совокупности всех конфигураций блока размера kn×kn много раз встретились стираемые.
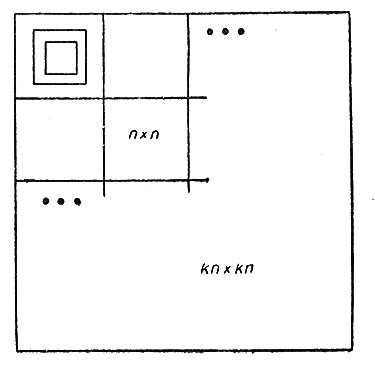
Рис. 6. Блок размера kn×kn, используемый при доказательстве теоремы 2
Зная состояние ячеек внутри блока размера kn×kn в момент T, мы можем определить состояние ячеек в момент Т+1 только внутри блока размера (kn - 2)×(kn - 2), ибо определить состояние ячеек, расположенных на границе блока, мы не можем. Поэтому, рассматривая блок размера (kn - 2)×(kn - 2), в который в момент Т+1 отобразится исходный блок размера kn×kn, мы сможем для обоих блоков подсчитать число возможных конфигураций. Для блока размера (kn - 2)×(kn - 2) это число равно A(kn-2)2, а для блока размера kn×kn оно равно A(kn)2, где А - число возможных состояний каждой ячейки.
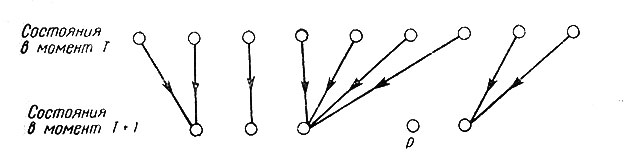
Рис. 7. Диаграмма, показывающая состояния блока в момент Т и состояния, в которые они переходят в момент времени T+1
Если в одном ряду (верхнем на рис. 7) изобразить все состояния исходного (т. е. размера kn×kn) блока, а в другом (нижнем на рис. 7) - все состояния блока, рассматриваемого в момент T+1, а затем указать, в какие состояния нижнего ряда отобразится каждое из состояний верхнего ряда, то мы заметим, что состояние, содержащее одну стираемую конфигурацию с, и другое состояние, содержащее конфигурацию, взаимно стираемую к с, в момент T+1 отобразятся в одно и то же состояние. Когда есть состояние, содержащее две копии стираемой конфигурации размера n×n, тогда четыре состояния, существующие в момент T, отобразятся в одно состояние, существующее в момент T+1. Вообще если мы имеем состояния, содержащие 5 копий стираемых конфигураций, то 2s состояний, существующих в момент T, отобразятся в одно состояние, существующее в момент T+1. Теперь осталось только показать, что потери в числе состояний вследствие стирания больше, чем потери вследствие несовпадения чисел A(kn)2 и A(kn-2)2.
Рассмотрим вместо числа состояний его логарифм. Логарифм отношения, которое указывает долю потерь в числе состояний, вызванных наличием граничного слоя, с ростом k растет приблизительно линейно. А если мы рассмотрим логарифм числа состояний, потерянных вследствие стирания, то увидим, что он увеличивается приблизительно пропорционально площади блока. Так как потери, вызванные стиранием, растут приблизительно пропорционально k2, то, выбрав k достаточно большим, можно показать, что эти потери будут больше, чем потери вследствие сокращения граничного слоя. Следовательно, должно существовать состояние р (показанное на рис. 7) блока размера (kn - 2)×(kn - 2), которого нельзя достигнуть ни из одного состояния блока размера kn×kn, рассматриваемого в момент T. Это состояние р и есть конфигурация райского сада, доказательство существования которой мы хотели получить.
Теперь дадим подробное доказательство теоремы 2. Рассмотрим отношение эквивалентности R для конфигураций блока размера n×n, которое определено для двух конфигураций, если они либо взаимно стираемы, либо представляют копии друг друга. Так как согласно условиям теоремы существует пара взаимно стираемых конфигураций размера n×n, то отношение R разбивает множество из An2 конфигураций размера n×n самое большее на Аn2 - 1 классов эквивалентности. Рассмотрим две конфигурации с и с' блока размера kn×kn. Будем говорить, что для конфигураций c и c' определено отношение R*, если для каждой из k2 подконфигураций размера n×n конфигурации с и подконфигурации того же размера, расположенной в соответствующем месте конфигурации с\ определено отношение эквивалентности R. Тогда и R* представляет собой отношение эквивалентности, а число классов эквивалентности по отношению R* не более (An2-1)k2. Так как любые две конфигурации, эквивалентные в смысле отношения R*, переходят в момент T+1 в одну и ту же конфигурацию, то для завершения доказательства теоремы остается только показать, что существует такое достаточно большое целое положительное число k, при котором выполняется неравенство
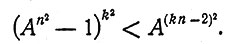
(1)
Для этого заметим, что так как A>1, n>1, то и An2>An2-1>0, поэтому
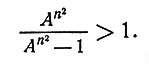
Следовательно, мы можем выбрать такое целое положительное k, что
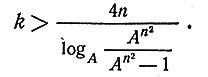
Тогда
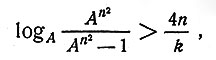
откуда
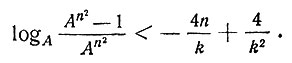
Из определения логарифма имеем
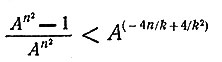
и, следовательно,
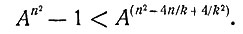
Возведя последнее неравенство в степень k2, мы получим неравенство
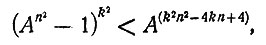
которое, как легко видеть, эквивалентно неравенству (1). Доказательство существования конфигураций райского сада закончено.
Такая конфигурация райского сад соответствует автомату, который не может возникнуть ни из какого прошлого состояния сотообразной вселенной, а может существовать лишь в момент T = 0. Такая конфигурация соответствует также машине, которую нельзя построить из доступных нам частей, но физическую структуру которой можно описать в виде определенного расположения этих частей.
Мы сделаем ряд предположений о природе сотообразной структуры, некоторые из них были замаскированы в данных уже определениях. Перечислим теперь все эти предположения:
- вселенная однородна;
- пространство и время квантованы (т. е. координаты и время принимают только целочисленные значения);
- в любой данный момент времени происходит взаимодействие лишь соседних элементов;
- вселенная представляет собой N-мерное евклидово пространство;
- законы, определяющие поведение вселенной, детерминированы;
- стирание возможно.
Из этих шести допущений (а возможно, и из других замаскированных, которые я не заметил) и было сделано заключение о существовании конфигураций райского сада. Каждое из этих предположений можно подробно исследовать, поскольку имеет смысл, может быть, попробовать доказать результат, аналогичный теореме 2, справедливый для некоторых математических моделей физического мира, удовлетворяющих не всем сделанным предположениям. В частности, если бы удалось доказать справедливость утверждения, аналогичного теореме 2, в некотором мире, отвечающем представлениям современной теоретической физики, то это могло бы иметь некоторый космологический интерес как указание на возможность существования таких состояний физического мира, которые можно описать, но которых никогда нельзя достичь.
Предположение (1) об однородности вселенной используется для того, чтобы из возможности стирания в одном месте вывести возможность стирания во многих других местах.
Предположение (2) о квантованности пространства и времени используется в приведенном выше методе доказательства, хотя, возможно, и существуют другие методы доказательства, основанные на интегрировании и применимые к непрерывному, а не дискретному миру, для которого мы провели доказательство.
Предположение (3) о зависимости поведения в любом месте от непосредственного прошлого и непосредственных соседей используется для того, чтобы ограничить влияние любой информации, приходящей в блок извне, только тонким пограничным слоем; это предположение соответствует допущению о том, что информация не может передаваться со скоростью, превышающей скорость света.
Предположение (4) о том, что вселенная есть N-мерное евклидово пространство, требуется только для того, чтобы иметь пространство, в котором можно найти область с объемом, больше объема тонкого слоя, ее ограничивающего, в любое наперед заданное число раз.
Предположение (5) о детерминированности законов поведения в рассматриваемом нами мире, исключает состояния, из которых можно попасть в последующий момент более чем в одно состояние. Если бы допускались вероятностные переходы, то они привели бы к ветвлению, и тогда для доказательства теоремы требовался бы такой метод, который позволил бы убедиться в том, что ветвление не будет оказывать большего влияния, чем стирание.
Предположение (6) жизненно важно для доказательства, и одна из сотообразных структур, уже определенная в этой статье, показывает, что при невыполнении этого предположения теорема неверна, даже если все остальные выполнены.
Предположение (6) противоречит классической механике, но не противоречит квантовой. Наоборот, предположение (5) противоречит квантовой механике, но согласуется с классической.
Дальнейшие проблемы. Существует много задач, относящихся к сотообразным структурам, сотообразным и кинематическим моделям самовоспроизведения. Некоторые из них мы сейчас сформулируем.
Можно ли вложить более точный смысл в утверждение о том, что одна машина менее тривиальна (или, что то же самое, более общая), чем другая, в отношении способности к самовоспроизведению? По-видимому, нет четко выраженной линии раздела между тривиальными и нетривиальными моделями самовоспроизведения. Можно ли формализовать понятие меньшей тривиальности в отношении способности к самовоспроизведению до такой степени, чтобы установить частичное упорядочение между машинами?
При изучении возможности зарождения жизни на земле [18] было бы желательно иметь метод расчета вероятности зарождения жизни при случайном взаимодействии между химическими соединениями, относящимися к неживой материи. Наверняка было бы очень интересно, если бы существовал некоторый способ определить, насколько сложной должна быть система (в частности молекула), образованная из частей, для того чтобы она обладала свойством самовоспроизведения (и более того, обладала бы способностью к эволюции, производя все более сложное потомство). Попытка в этом направлении была предпринята Джекобсоцом [6], когда он хотел для некоторых из предложенных им моделей охарактеризовать сложность системы количеством битов информации.
Пусть в сотообразной структуре существует конфигурация райского сада. Каков тогда должен быть размер наименьшего блока, содержащего конфигурацию райского сада? Хотя метод доказательства теоремы 2, приведенный в статье, дает очень большой размер для блока, содержащего конфигурацию райского сада, но для сотообразной структуры, которую я детально исследовал, конфигурация райского сада могла содержаться в блоке размера 5×5 (или даже меньшего размера).
При какой простоте сотообразной структуры (выраженной в числе состояний или в какой-либо другой мере сложности) в ней еще могут существовать нетривиальные самовоспроизводящиеся конфигурации?
Может ли сотообразная структура иметь самовоспроизводящиеся конфигурации, не имея при этом стираемых конфигураций?
Для всех сотообразных структур, имеющих n состояний, желательно получить оценки сверху и снизу (или, может быть, точные значения) числа структур, обладающих стираемыми конфигурациями, и числа структур, обладающих самовоспроизводящимися конфигурациями. В частности, можно ли доказать, что при увеличении n доля сотообразных структур, обладающих стираемыми конфигурациями, стремится к единице?
Каковы размеры наименьшего внутреннего блока стираемой конфигурации (соответствующего F на рис. 4)? Во всех сотообразных структурах, которые были подробно исследованы, наименьший внутренний блок стираемой конфигурации состоял только из одной ячейки. Можно ли доказать, что это всегда так?
Каким образом можно добиться того, чтобы большие машины как в сотообразной, так и в кинематической моделях осуществляли самовоспроизведение не последовательно, а параллельно? Это позволило бы за один момент времени изготовить сразу много частей машины вместо предложенного Пенроузом [20], фон Нейманом [16] и Джекобсоном [6] более медленного изготовления одной части в один момент.
Краткий обзор других работ. Список работ от [1] до [31] включительно претендует на то, чтобы полностью охватить все, что было написано о моделях машин, осуществляющих самовоспроизведение (т. е. о самовоспроизводящихся автоматах). Ссылки от [32] до [48] охватывают только очень малую часть литературы, в какой-то степени связанной с вопросом о конечных автоматах, последовательных и итеративных цепях. В следующих абзацах кратко охарактеризованы работы, не цитированные в статье.
Коммутационные цепи, конфигурации которых периодически заполняют все гс-мерное евклидово пространство, представляют собой электрическую реализацию того, что в этой статье названо сотообразными структурами, а сами цепи обычно называются итеративными. В работах [2, 33] и [5] рассматриваются такие цепи для произвольного п, а в работах [47] и [38] рассматриваются возможности применения машин, построенных из таких итеративных цепей главным образом при n = 2. Одномерным итеративным цепям посвящены работы [37, 40, 41, 34].
Работы [2, 3] посвящены сотообразным структурам, сотообразным моделям самовоспроизведения и некоторым задачам, связанным с моделями фон Неймана.
Работа [13] дает частичное описание модели, являющейся по своим характеристикам промежуточной между кинематической и сотообразной моделями фон Неймана. Исходя из нескольких аксиом для описания поведения машин, способных произвести другие машины, и на основании теории рекурсивных функций в работе [14] дано доказательство того, что машины могут создавать свои улучшенные варианты, но улучшение здесь понимается как способность отпечатывать более широкий класс истинных теорем, поэтому работа представляет больший интерес для логика, чем для биолога.
В работах [1, 10, 22, 23, 24] исследуются модели Пенроуза и осуществляется их дальнейшая разработка.
Улам [28] ставит проблему, в некоторой степени аналогичную проблеме, решенной теоремой 2. Некоторые практические и экономические вопросы, относящиеся к конструированию реально работающих моделей самовоспроизводящихся машин, обсуждаются в [9] и [31].
В работе [7] наиболее подробно рассматривается сотообразная модель самовоспроизведения, предложенная фон Нейманом. Шеннон [27] дает общее изложение идей фон Неймана, а статьи [4, 8, 26, 30] содержат некоторые упоминания о самовоспроизводящихся машинах, хотя в этих статьях главным образом рассматриваются другие типы машин.
Улам [29] рассматривает комбинаторные проблемы описания конфигураций, возникающих в различных простых сотообразных структурах.
Статьи [35, 36, 43, 45, 46, 48] касаются абстрактной теории конечных автоматов без всякого упора на какие-либо реализации этих автоматов в виде электрических цепей. Электрические цепи, реализующие такие машины, называются последовательными цепями, они рассматриваются в статьях [32, 34, 39, 40, 42, 44]. Много ссылок на другие работы в области последовательных цепей, итеративных цепей и конечных автоматов содержится в [32, 35, 36, 41, 42, 45, 48] и других работах.
Благодарности. Автор хотел бы выразить свою признательность К. Е. Шеннону, советам которого он обязан формулировкой теоремы 2 и основной идеей метода ее доказательства. Автор также хотел бы выразить свою благодарность за советы, данные Х. О. Поллаком, Е. Н. Гильбертом и Дж. Б. Крускалом, в результате которых значительно упростилось утверждение и доказательство неравенства (1) (по сравнению с тем, что было в более раннем наброске статьи).
Литература
- Abercrombie M., Introduction to replication; New Biology, № 31, Penguin Books, Harmondsworth, England, 1960, стр. 10-24.
- Burks A. W., Computation, behavior and structure in fixed and growing automata, Self-organizing systems, New York, 1960, стр. 283-311.
- Burks A. W., Summary of states and transition rules for von Neumann's self-reproducing automaton; готовится к изданию вместе с [16].
- Burks A. W., Wang Hao, The logic of automata, J. Assoc. Comput. Mack, 4 (1957), № 2, 193-218, № 3, 279-297.
- Church A., Application of recursive arithmetic to the problem of circuit synthesis; Summaries of talks presented at the Summer Institute of Symbolic Logic, Cornell Univ., 1957, 2 изд., стр. З- 50, Communications Research Division, Institute for Defense Analyses, Princeton, New York, 1960.
- Jacobson H., On models on reproduction, American Scientist, 46, № 3 (1958), 255-284. (Русский перевод: Джекобсон Г. О., О моделях самовоспроизведения, Кибернетический сборник, вып. 7, ИЛ, М., 1963.)
- Kemeny J. G., Man viewed as a machine, Sci Amer., 192 (1955), № 4, 48-53; исправления там же, № 6, 6. Частично перепечатано в Automatic control, New York, 1955, стр. 132-146.
- Lofgren L., Automata of high complexity and methods of increasing their reliability by redundancy; Actes du Congres International de Cybernetique, Namur, 26-29 Juin 1956, стр. 493- 511, Paris, 1958. Опубликовано также в Information and Control, 1, №2 (1958), 127-147.
- Moore E. F., Artificial living plants, Sci. Amer., 195, № 4 (1956), 118-126.
- Moore E. F., Review of four papers by Penrose [19, 20, 21, 22], Trans. IRE Professional Group on Electronic Computers, EC-8, № 3 (1959), 407-408.
- Moore E. F., Machine models of self-reproduction, Abstract 560-52, Notices Amer. Math. Soc, 6 (1959), 622-623.
- Morowitz H. J., A model of reproduction, American Scientist, 47, № 2 (1959), 261-263.
- Myhill J., Self-reproducing automata; отпечатано на машинке, Institute for Advanced Study (1959).
- Myhill J., Possibilities of favorable mutation in self-reproducing automata; курс лекций, прочитанный в Мичиганском университете в июне 1960 г.
- vom Neumann J., Theory and organization of complicated automata; пять лекций, прочитанных в декабре 1949 г. Готовится к изданию в Univ. of Illinois Press.
- von Neumann J., The theory of automata: Construction, reproduction, and homogeneity, готовится к изданию в Univ. of Illinois Press.
- von Neumann J., The general and logical theory of automata, Cerebral mechanisms in behavior, New York, 1951, стр. 1-48. Частично перепечатано в The world of mathetatics, New York, 1956, стр. 2070-2098.
- Опарин А. И., Возникновение жизни на Земле, изд. АН СССР, М., 1957.
- Penrose L. S., Penrose R., A self-reproducing analogue, Nature, 179, № 4571 (1957), 1183.
- Penrose L. S., Mechanics of self-reproduction, Ann. Human Genetics, 23 (1958), part I, 59-72.
- Penrose L. S., Automatic mechanical self-reproduction, New Biology, № 28, Penguin Books, Harmondsworth, England, 1959, стр. 92-117.
- Penrose L. S., Self-reproducing machines, Sci. Amer., 200, №6, (1959), 105-114, 202.
- Penrose L. S., Developments in the theory of self-replication New Biology, № 31, Penguin Books, Harmondsworth, England, 1960, стр. 57-66.
- Penrose L. S., Automatic mechanical self-replication, текст к цветному фильму, снятому Н. A. Cresswell, Hemel Hempstead, Herts., England, 1958.
- Rosen R., On a logical paradox implicit in the notion of a self-reproducing automaton, Bull. Math. Biophys., 21 (1959), 387-395.
- Shannon С. Е., Von Neumann's contributions to automata theory, Bull. Amer. Math. Soc, 64, № 3 (1958), part 2, 123-129. (Русский перевод: Шеннон К., Работы по теории информации и кибернетике, ИЛ, М., 1963, стр. 232-239.)
- Shannon С. Е., Computers and automata, Proc. IRE, 41, №10 (1953), 1234-1241. (Русский перевод: Шеннон К., Работы по теории информации и кибернетике, ИЛ, М., 1963, стр. 162-180.)
- Ulam S. M., A collection of mathematical problems, Inter-science, New York, 1960; особенно "A problem on matrices arising in the theory of automata", стр. 30. (Русский перевод: Улам С, Нерешенные математические задачи, "Наука", М., 1964.)
- Улам С., Некоторые математические проблемы, связанные с процессом роста фигур; настоящий сборник, стр. 63-77.
- Wang Hao, Universal Turing machines: an exercise in coding, 2. Math. Logik Grundlagen Math., 3, № 2 (1957), 69-80.
- Watkins D. A., Moore E. F., Letters, Sci. Amer., 196, № 2, (1957), 8-10.
- Айзерман М. А., Гусев Л. А., Розоноэр Л. И., Смирнова И. М. и Таль А. А., О методах реализации конечного автомата, тактность которого определяется изменением состояния входа, Автоматика и телемеханика, 12 (1960), 1576-1594.
- Burks A. W., The logic of fixed and growing automata, Proceedings of an International Symposium on the Theory of Switching, 2-5 April 1957, I, The Annals of the Computation Laboratory of Harvard University, Vol. 29, pp. 147-188, Harvard Univ. Press, Cambridge, Mass., 1959.
- Caldwell S. H., Switching circuits and logical design, New York, 1958.
- Elgot С. С. Decision problems of finite automata design and related arithmetics, Trans, Amer. Math. Soc, 98 (1961), 21-51.
- Ginsburg S., Connective properties preserved in minimal state machines, J. Assoc, Comput. Mach.K 7, № 4 (1960), 311-325.
- Hennie F. C., Analysis of bilateral iterative networks, Trans. IRE Professional Group on Circuit Theory, CT-6, № 1, (1959), 35-45.
- Holland J., A universal computer capable of executing an arbitrary number of sub-programs simultaneously, Proceedings of the Eastern Joint Computer Conference, December 1-3, 1959, № 16, стр. 120-132.
- Huffman D. A., The synthesis of sequential switching circuits, J. Franklin Inst., 257, № 3 (1954), 161-190; № 4, 275-303.
- Huffman D. A., Canonical forms for information-lossless finite-state logical machines, Trans. IRE Professional Group on Circuit Theory, CT-6 (1959), supplement, 41-59.
- McCluskey E. J., Jr., Assignment of carry variables in iterative networks, Trans Amer. Inst. Elec. Engrs. I. Communication and Electronics, 79, № 52 (1961), 772-778.
- Moisil Gr. C., Algebraic theory of automatic machines, Editu-ra Technica, Bucharest, 1959.
- Moore E. F., Gedanken-experiments on sequential machines, Automata Studies; Annals of Mathematics Studies, № 34, Princeton, New York, 1956, стр. 129-153. (Русский перевод: Мур Э. Ф., Умозрительные эксперименты с последовательностными машинами, сб. "Автоматы", ИЛ, М., 1956.)
- Muller D. E., Bartky W. S., A theory of asynchronous circuits; Proceedings of an International Symposium on the Theory of Switching, 2-5 April 1957, Part I; The Annals of the Computation Laboratory of Harvard University, Vol, 29, pp. 204-243, Harvard Univ. Press., Cambridge, Mass., 1959.
- Sundaram Sashu, Reed В., Linear graphs and electrical networks, Mass., 1961, особенно стр. 250-267, 301-310.
- Rabin M. O., Scott D., Fin'te automata and their decision problems, IBM J. Res. Develop., 3, № 2 (1959), 114-125. (Русский перевод: Рабин М. О., Скотт Д., Конечные автоматы и задачи их разрешения, Кибернетический сборник, вып. 4, ИЛ, М" 1962.)
- Unger S. H., A new computer oriented toward spatial problems, Proc. IRE, 46, № 10 (1948), 1744-1750.
- Wang H a o, Circuit synthesis by solving sequential Boolean equations, Z. Math, Logik Grundlagen Math., 5 (1959), № 3/4, 291-322.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'