§ 17. Перегибая лист бумаги

Среди множества возможных действий с бумагой особое место занимает операция ее перегибания. Одним из достоинств этой операции является то, что ее можно производить, не имея под рукой никаких дополнительных инструментов - ни линейки, ни циркуля, ни даже карандаша. Этим вы, конечно, неоднократно пользовались, когда складывали из бумаги пилотку, самолет, кораблик и т. п.

Практические свойства бумаги порождают своеобразную геометрию, с элементами которой мы познакомим вас в настоящем параграфе. Роль линий в этой геометрии будут играть края листа и складки, образующиеся при его перегибаниях, а роль точек - вершины углов листа и точки пересечения складок друг с другом или с краями листа. Оказывается, возможности операции перегибаний листа очень велики. То, что они включают в себя всю геометрию одной линейки, не вызывает сомнений. Но они в определенной степени- таят в себе также и возможности циркуля, хотя и не позволяют проводить непосредственно дуги окружности.

Заметим, что при реальной работе с бумагой нужно учитывать следующие обстоятельства. Если складывать лист бумаги в несколько раз, то сами складки получаются все менее и менее четкими из-за того, что настоящая бумага имеет некоторую, пусть незначительную, но ненулевую толщину. Этот эффект иногда начинает проявляться уже при втором перегибании. Следовательно, решая задачи этого параграфа, вы должны беспокоиться о том, чтобы при реализации решений бумагу приходилось складывать по возможности в меньшее число раз. Кроме того, не будем закрывать глаза и на то, что внешний вид бумаги несколько портится от дополнительных складок. Поэтому поищите более экономные в этом смысле построения.

Каждый, наверное, уже давно привык к тому, что бумага перегибается всегда по прямой линии, а не по окружности и не по какой-нибудь другой кривой. Попробуйте найти причину этого явления.

На листе бумаги отмечены две точки А и В. Как с помощью перегибаний этого листа разделить отрезок АВ пополам?

Как с помощью перегибаний листа бумаги провести прямую, перпендикулярную данной прямой и проходящую через данную точку?

Как с помощью перегибаний листа бумаги провести прямую, параллельную данной прямой и проходящую через данную точку?

Как с помощью перегибаний найти центр вырезанного из бумаги круга? Можно ли найти центр круга, нарисованного на непрозрачной бумаге?

На листе бумаги проведена прямая, а также даны центр окружности и некоторая точка на ней (сама окружность не нарисована). Как с помощью перегибаний бумаги найти точки пересечения воображаемой окружности с проведенной прямой?

Из бумаги вырезан треугольник. Укажите, как с помощью перегибаний найти следующие линии и точки этого треугольника: биссектрису данного угла; высоту, опущенную из данной вершины (если углы при двух других вершинах острые); медиану, проведенную к данной стороне; центр вписанной окружности- центр описанной окружности (для остроугольного треугольника).

У вас в руках оказался лист бумаги неправильной формы, а вы хотите с помощью перегибаний получить из него бумажный прямоугольник. Один из простейших способов сделать это состоит в последовательном проведении сначала какой-либо прямой АВ, затем перпендикуляра ВС к ней, затем перпендикуляра CD к полученной прямой и, наконец, перпендикуляра DA к прямым CD и АВ (рис. 87). Однако если проводить перпендикуляры так, как это описано в решении задачи 17.3, то слишком много бумаги уйдет в отходы. Дело в том, что проведение перпендикуляров описанным способом предполагает наличие достаточно больших участков дайной прямой как с одной, так и с другой сторону отданной точки (иначе точность построения сильно падает: таким образом на рис. 87 перпендикуляр к прямой АВ через точку В точно провести практически не удается).

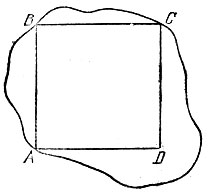
Рис. 87

Придумайте другой способ проведения перпендикуляров, пользуясь которым можно свести расход бумаги при выравнивании ее краев к минимуму (например, реализовать построение прямоугольника ABCD, изображенного на рис. 87).

Из бумаги вырезан прямоугольник. Получите из него квадрат со стороной, равной меньшей стороне прямоугольника.

Из бумаги вырезан прямоугольник. Укажите способ получения из него различных равнобедренных треугольников и, в частности, равностороннего треугольника.

Из бумаги вырезан квадрат ABCD. Как при помощи перегибаний вписать в него равносторонний треугольник AEF, имеющий с квадратом ровно одну общую вершину А (рис. 88).

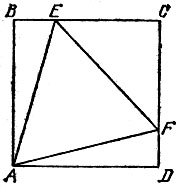
Рис. 88

Из листа бумаги, имеющего форму равностороннего треугольника, с помощью перегибаний нужно получить правильный шестиугольник. Как это сделать?

Из листа бумаги, имеющего форму квадрата, с помощью перегибаний нужно получить правильный восьмиугольник. Как это сделать?

С помощью перегибаний произвольного бумажного треугольника продемонстрируйте тот факт, что сумма углов при его вершинах равна 180°.

Если вам понадобилось чем-нибудь заложить страницу в записной книжке так, чтоб закладка торчала, но под рукой нет никакого подходящего предмета, то подумайте над вопросом, нельзя ли перегнуть саму страницу, нигде не разрывая ее, чтобы в результате какой-то ее краешек торчал из закрытой записной книжки.

Можно ли сложить многоугольник, вырезанный из бумаги, так, чтобы периметр полученной фигуры оказался больше, чем периметр исходного многоугольника?

Из бумажной полоски шириной 1 с помощью нескольких перегибаний получите квадрат, у которого диагональ равна 2.

Из бумажной полоски шириной 1 с помощью перегибаний получите правильный шестиугольник, у которого расстояние между параллельными сторонами равно 2.

Попробуйте завязать бумажную полоску с параллельными краями узлом так, чтобы после ее стягивания и разглаживания в узле образовался пятиугольник ABCDE, изображенный на рис. 89. Докажите, что этот пятиугольник правильный.

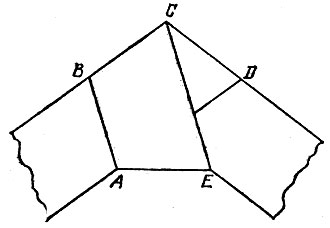
Рис. 89

Решения

17.1. Обычно бумагу перегибают следующим образом: одну часть листа накладывают на другую и, прижав их друг к другу в определенном месте одной рукой, разглаживают оба листа другой рукой до образования складки. Если при этом некоторые две точки А и В бумаги оказались прижатыми друг к другу, то любая точка С складки будет равноудалена от точек А и В, так как отрезки АС и ВС после разглаживания окажутся прижатыми друг к другу. Поскольку множество таких точек С совпадает с серединным перпендикуляром к отрезку АВ, то полученная складка будет прямой линией. Заметим, что любые точки листа бумаги, которые оказываются прижатыми друг к другу после его перегибания по некоторой прямой, являются симметричными относительно этой прямой на развернутом листе.

17.2. Перегнем лист бумаги по прямой линии, проходящей через точки А и В так, чтобы сами точки остались на видимой стороне бумаги после перегибания (рис. 90). Тогда, прижав друг к другу точки А и В неразвернутого листа и разгладив этот лист, мы получим искомую точку С на прямой АВ, равноудаленную от А и В (решение задачи 17.1).

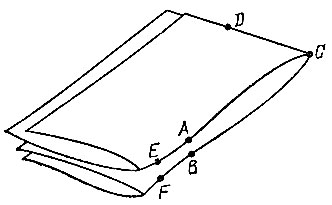
Рис. 90

17.3. Перегнем лист бумаги по данной прямой так, чтобы данная точка D осталась на видимой стороне листа. Затем, не разворачивая лист бумаги, перегнем его еще раз по прямой, проходящей через точку D, проследив при этом за тем, чтобы некоторые точки А и В данной прямой совместились (рис. 90). Тогда полученная прямая CD будет перпендикулярна прямой АВ, поскольку углы ACD и BCD в силу симметрии равны друг другу и составляют в сумме развернутый угол АСВ.

В описанном здесь построении после первого перегибания бумагу можно полностью развернуть, а затем перегнуть по прямой, проходящей через точку D, проследив за тем, чтобы совместились некоторые другие точки прямой АВ, одна из которых лежит на самом краю листа.

17.4. Проведем сначала перпендикуляр к данной прямой к, как описано в решении задачи 17.3, а потом проведем перпендикуляр к полученной прямой, проходящий через иную точку. Последняя прямая будет параллельна данной, так как обе они перпендикулярны одной и той же прямой.

17.5. Если круг вырезан из бумаги, то, перегнув его полам по некоторому диаметру АВ (для этого нужно, чтобы, как на рис. 91, при наложении две полуокружности вместились друг с другом), а затем перегнув лист еще раз так, чтобы совместились точки А и В, мы получим центр О круга (см. задачу 17.2).

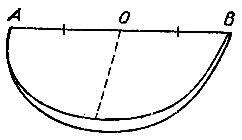
Рис. 91

Если же круг нарисован на непрозрачной бумаге, то перегнем лист по какой-нибудь хорде и по серединному перпендикуляру АВ к ней, а затем найдем середину О этого перпендикуляра (см. задачи 17.2, 17.3). Точка О будет центром круга, так как АВ - его диаметр (серединный перпендикуляр к некоторой хорде).

17.6. Перегнем бумагу по прямой, проходящей через Центр О окружности и данную ее точку А, так, чтобы точки О и А оказались на видимой стороне листа (рис. 92). Теперь перегнем лист еще раз по линии, проходящей через точку О, следя за тем, чтобы точка А совместилась с какой-нибудь точкой В проведенной прямой. Тогда точка В будет удалена на расстояние ОА от центра окружности, т. е. будет лежать как на прямой, так и на окружности. Подбирая другой угол между первой и второй линиями перегиба, мы получим еще одну точку С пересечения прямой с окружностью (если, конечно, такие точки вообще существуют).

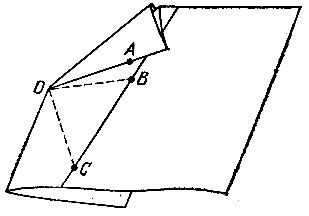
Рис. 92

17.7. Для построения биссектрисы угла А треугольника ABC перегнем лист бумаги так, чтобы сторона АВ пошла по стороне АС. Тогда линия сгиба будет осью симметрии угла ВАС, т. е. его биссектрисой. Высота проводится тем же методом, что и в решении задачи 17.3, где опускается перпендикуляр из данной точки (вершины треугольника) к данной прямой (противолежащей стороне треугольника). Для проведения медианы к стороне ВС данного треугольника сначала найдем середину этой стороны (см. задачу 17.2), а затем соединим ее линией сгиба с вершиной А треугольника ABC. Центр вписанной окружности лежит на пересечении биссектрис каких-нибудь двух углов треугольника. Для нахождения центра описанной окружности достаточно провести серединные перпендикуляры к каким-нибудь двум сторонам треугольника (см. задачи 17.3) и определить точку их пересечения.

17.8. Примерно по середине листа проведем две перпендикулярные прямые (линии сгиба) EF и GH, параллельные сторонам будущего прямоугольника ABCD и пересекающиеся в точке О (рис. 93). Приложим сверху край EF листа, перегнутого предварительно по прямой EF, к той части исходного листа, которая содержит точку G, и проследим, чтобы точка О оказалась прижатой к лучу OG. Тогда, перегнув вдоль листа нижнюю часть листа, мы получим прямую AD. Аналогично с другой стороны от прямой EF получаем прямую ВС. Приложив также край GH листа, перегнутого по прямой GH, к той части исходного листа, которая содержит точку Е, и проследив, чтобы точка О оказалась прижатой к лучу ОЕ и чтобы линия GH пересекла обе построенные ранее линии AD и СВУ мы получим сторону АВ прямоугольника. Аналогично получаем противоположную его сторону CD. Для доказательства того, что построенный четырехугольник действительно является прямоугольником, достаточно проверить, что прямые АВ и CD параллельны прямой EF, а прямые AD и ВС - прямой GH.

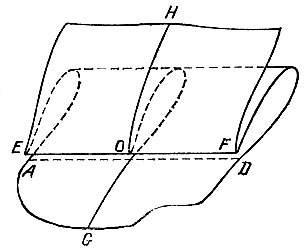
Рис. 93

17.9. Перегнем прямоугольный лист бумаги по биссектрисе одного из его углов BAD, т. е. так, чтобы сторона АВ прямоугольника ABCD пошла по соседней с ней стороне AD, а линия сгиба пересекла какую-то третью сторону в точке Е (рис. 94). Пусть меньшая сторона АВ оказалась наложенной сверху на большую сторону AD. Тогда, перегнув нижнюю часть листа вдоль линии BE, мы получим квадрат ABEF. Действительно, в четырехугольнике ABEF выполнены равенства ∠ ABE = ∠ BAF = 90°, АВ = ВЕ (ибо ∠ ВАЕ = 45° = ∠ AEB), AB = AF, BE = FE, следовательно, все стороны этого четырехугольника равны, а углы прямые.

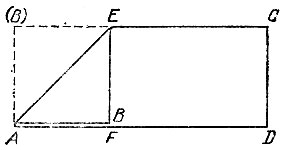
Рис. 94

17.10. Перегнем данный прямоугольник ABCD по серединному перпендикуляру EF, скажем, к меньшей стороне AD (рис. 95). Не разворачивая лист, перегнем его еще раз по любой линии, пересекающей отрезки АЕ и EF. Тогда после разворачивания последняя линия сгиба, которая пройдет как по прямоугольнику AEFB, так и по прямоугольнику DEFC, вместе с прямой AD образует равнобедренный треугольник (в силу его симметрии относительно прямой EF).

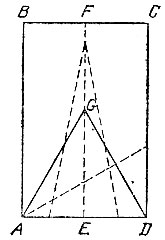
Рис. 95

Для построения равностороннего треугольника перегнем прямоугольник ABCD по линии, проходящей через вершину А, так, чтобы точка D совместилась с какой-нибудь точкой G отрезка EF. Тогда треугольник ADG будет равносторонним, поскольку в силу построения имеем AD = AG = GD.

17.11. Проведем серединный перпендикуляр к стороне AD квадрата ABCD, а затем перегнем квадрат по линии, проходящей через точку А, так, чтобы точка В совместилась с какой-нибудь точкой G проведенного перпендикуляра (рис. 96). Тогда линия сгиба пересечет сторону ВС в точке Е, а если перегнуть квадрат по диагонали АС, то точка Е совместится с точкой F. Докажем, что треугольник AEF равносторонний. Действительно, так как треугольник ADG равносторонний (ибо DG = AG = AB = AD), то ∠ DAG = 60°, ∠ BAG = 90° - 60° = 30°, ∠ DAF = ∠ BAE = ∠GAE = 15°, ∠ FAE = 90° - 15° - 15° = 60° и, кроме того, AF = AE.

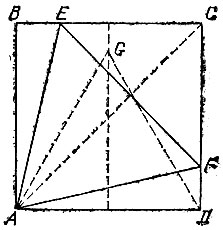
Рис. 96

17.12. Проведя две биссектрисы равностороннего треугольника ABC (см. задачу 17.7), мы найдем его центр О. Загнем углы треугольника так, чтобы их вершины совместились с точкой О (рис. 97). Тогда полученная фигура и будет представлять собой правильный шестиугольник. В самом деле, все шесть треугольников, из которых составлен шестиугольник, являются равносторонними (их равнобедренность вытекает из симметрии всей фигуры относительно биссектрис исходного треугольника ABC, а равенство каждого из углов по 60° следует из равенства 60° каждого из углов при вершинах А, В, С и равенства друг другу трех оставшихся углов с вершинами в точке О).

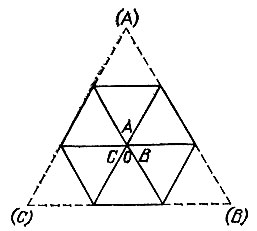
Рис. 97

17.13. Проведем диагонали квадрата ABCD, серединный перпендикуляр к стороне AD и биссектрисы углов между диагоналями и этим перпендикуляром. Загнем углы квадрата так, чтобы линии сгиба проходили через точки пересечения биссектрис со сторонами квадрата, а вершины углов А, В, С, D оказались на соответствующих диагоналях (рис. 98). Тогда полученная фигура и будет представлять собой правильный восьмиугольник. В самом деле, все углы, под которыми видны из центра квадрата стороны восьмиугольника, равны между собой (каждый такой угол составлен из двух углов между проведенными выше биссектрисой и диагональю), а кроме того, равны и все расстояния от вершин восьмиугольника до центра квадрата (равные длине той же биссектрисы).

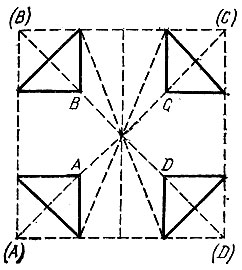
Рис. 98

17.14. Проведем высоту AD треугольника ABC, опущенную из вершины А его наибольшего угла. Теперь загнем все три угла треугольника так, чтобы их вершины совместились с точкой D (рис. 99). Тогда углы при вершинах треугольника без наложений друг на друга составят в сумме развернутый угол с вершиной D, равный 180°.

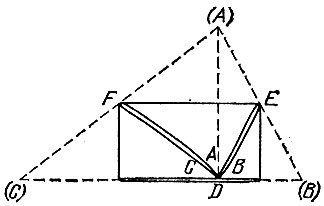
Рис. 99

Для доказательства этого заметим, что линия сгиба EF, будучи серединным перпендикуляром к высоте AD, является средней линией треугольника ABC. Поэтому имеют место равенства DE = AE = BE, DF = AF = CF, т. е. треугольники BED, CFD равнобедренные и

а значит, произведенные выше перегибания этих треугольников действительно приведут к указанным совмещениям.

17.15. Один из возможных способов перегибания страницы изображен на рис. 100.

Рис. 100

17.16. После каждого перегибания периметр фигуры не увеличивается. Действительно, при наложении одной части фигуры на другую появляется новая часть периметра, а именно линия сгиба. Однако другая часть периметра исчезает, т. е. оказывается внутренней для полученной фигуры. Исчезающая часть периметра содержит ломаную, соединяющую концы линии сгиба, или несколько таких ломаных, если линия сгиба не сплошная (рис. 101). Таким образом, добавляемая часть периметра никогда не превосходит его теряющейся части, поэтому периметр не увеличивается при однократном и, стало быть, при многократном складывании бумажного многоугольника.

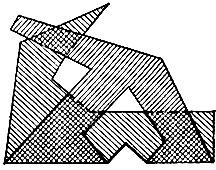
Рис. 101

17.17. Пусть полоска имеет ровный торец АВ, перпендикулярный краю полоски (рис. 102). Перегнув ее по биссектрисе угла А, мы получим квадрат ABA₁В₁. Перегнув оставшуюся часть полоски с торцом A₁B₁ по биссектрисе угла А₁, мы получим квадрат А₁В₁А₂В₂.

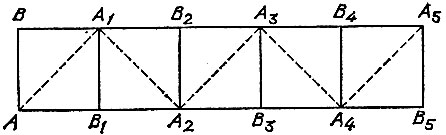
Рис. 102

Действуя в таком же духе и далее, мы найдем точки А₃, В₃, А₄, В₄, А₅, В₅. Теперь обрежем полоску по линиям AА₁ и А₄А₅ и получим параллелограмм AА₁А₅А₄, который можно сложить так, как показано на рис. 103 (полученный при этом квадрат АА₁А₂А₃ даже не будет распадаться).

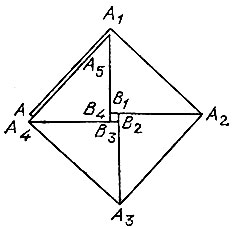
Рис. 103

17.18. Пусть полоска имеет ровный торец АВ, перпендикулярный краю АЕ полоски (рис. 104). Проведем серединный перпендикуляр к отрезку АВ и перегнем полоску по некоторой линии АС так, чтобы точка В совместилась с какой-то точкой D серединного перпендикуляра. Тогда треугольник ABD равносторонний (ибо AB = AD = BD) откуда ∠ BAD = 60° и ∠ CAE = ∠ DAE + ∠ CAD = (90° - ∠ BAD) + ∠ BAD = 60°. Перегибая полоску по перпендикуляру к краю АЕ, проходящему через точку С, получаем равносторонний треугольник ACB₁. Перегибая полоску по перпендикуляру к краю АЕ, проходящему через точку B₁, получаем равносторонний треугольник СВ₁А₁.

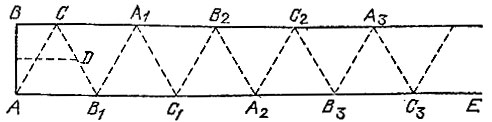
Рис. 104

Действуя в таком же духе и далее, мы найдем точки С₁, В₂, A₂, С₂, В₃, A₃, С₃. Теперь отрежем полоску по линиям AС, A₃С₃ и получим трапецию АСА₃С₃, которую можно сложить так, как показано на рис. 105 (полученный при этом шестиугольник ACA₁C₁A₂C₂ даже не будет распадаться).

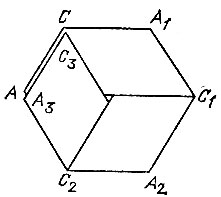
Рис. 105

17.19. Заметим, что при перегибании бумажной полоски с параллельными краями по некоторой поперечной линии АЕ внутренние накрест лежащие равные углы AED и EAF (рис. 106) превращаются в односторонние, но по-прежнему равные углы AED и ЕАВ. По этой причине имеем равенства

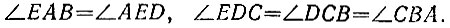
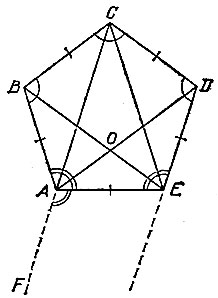
Рис. 106

В силу параллельности прямых АС и ED, ЕС и АВ, AD и ВС, BE и CD заключаем, что четырехугольники ABCD, АВСЕ, ACDE и BCDE являются трапециями, причем две последние равнобедренными, а четырехугольник BCDO является параллелограммом с одинаковыми высотами (равными ширине полоски), т. е. ромбом. Поэтому имеем

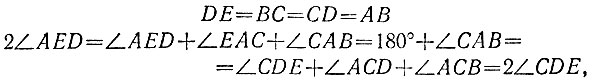
откуда получаем ∠ AED = ∠ CDE, AE = CD, а значит, все стороны пятиугольника ABCDE равны между собой и все его углы одинаковы. Мы доказали, что пятиугольник, образующийся в узле бумажной полоски, правильный.