12. Годы войны. 1940-1945

Осенью 1939 года, возвратившись после отпуска в МТИ, я попробовал разобраться в том, что же происходит в мире. Ситуация была такова, что рассчитывать на что-нибудь хорошее не приходилось. В научных и промышленных кругах большинство понимало, что Соединенные Штаты, так же как и другие великие державы, в конце концов будут втянуты в мировую войну. Поэтому каждый заранее стремился найти такой участок работы, на котором в этом случае можно было бы применить свои силы.

Из-за близорукости я даже в молодости не мог попасть на действительную военную службу; с годами же мои шансы, естественно, не увеличились. Я не мыслил себя администратором, и никому не пришло бы в голову, что я обладаю такого рода способностями. Очевидно, мне не оставалось ничего другого, как обратиться к какому-то виду научно-исследовательской работы.

Во время первой мировой войны я прошел курс ученичества в области баллистических расчетов. Такого рода расчеты необходимы для составления артиллерийских таблиц стрельбы, в которых указывается зависимость дальности стрельбы и других связанных с нею констант от угла прицела орудия, величины заряда, веса снаряда и т. п. Кроме того, в последние годы я много работал вместе с инженерами-электриками. Исходя из всего этого, я предполагал, что в случае войны мне следует, очевидно, заняться какой-то деятельностью, так или иначе связанной с применением вычислительной математики к электротехническим проблемам. Такая перспектива представлялась мне тем более реальной, что совместная работа с Ли позволила мне заглянуть в тайны конструкторского творчества.

В этом отношении все было ясно, неясным оставалось только, откуда раздастся призывный глас. Когда после выматывающего душу ожидания эпохи Sitzkrieg'a^* начали приходить тревожные известия о военных успехах и грозных планах Германии, большинство из нас пришло к убеждению, что основная задача Америки - сохранить Англию в качестве активного противника Гитлера до тех пор, пока мы сами не сможем вступить в войну. А для этого в первую очередь мы должны были помочь англичанам справиться с подводными лодками и налетами бомбардировщиков.

^* (Сидячая война (нем.). )

К счастью, блистательным изобретением радара Англия сама указала нам наилучший из всех возможных способов помощи. МТИ начал заниматься исследованиями в области радаров, как только появилась сама эта идея, т. е. еще до начала войны в Европе и задолго до вступления в войну Соединенных Штатов. Но в то время, о котором идет сейчас речь, казалось, что проблемы, связанные с радарными установками, касаются только узкого круга инженеров-специалистов, а я не принадлежал к их числу.

Поток беженцев из Германии в какой-то момент усилился, а потом совсем иссяк. Последняя струйка эмиграции состояла, как мне казалось, из людей, резко отличавшихся но своим моральным качествам от тех, кто приехал в самом начале. Гитлеровский давильный пресс вытеснил из Европы какое-то количество людей, которые пытались убедить нас в неотвратимости нацизма. Платные пропагандисты не проявили бы большего рвения. В конце концов стало очевидно, что в добавление к богатой культурной жатве, состоящей из замечательных мужчин и женщин, преследуемых в Европе и обогативших собой нашу научную жизнь, мы получили еще тех, кто возражал против фашизма только потому, что фашизм возражал против них.

Между тем в положенное время наступили летние каникулы, и, несмотря на разразившуюся рядом катастрофу, мы постарались сделать нашу жизнь как можно более веселой. Человек все равно не может постоянно жить в атмосфере уныния.

Семью Ингамов из английского Кембриджа война застала в Америке, и они стали нашими летними соседями. Мы делили с ними радости прогулок по горам и купаний в пруду Беар Кегли.

В то лето венгерский математик Эрдеш, японский математик Какутани и английский математик Стоун нанесли нам не совсем обычный, но очень интересный визит. Гуляя по Лонг Айленду^*, они попали в неприятную историю, случайно подойдя слишком близко к радиолокационной установке. В тот же вечер их посадили в тюрьму как подозрительных иностранцев и освободили только после того, как тюремное начальство связалось с их покровителем профессором Вебленом из Припстопского университета. По окончании этого невеселого приключения они приехали в Ныо-Хемпшир, и на веранде нашего дома состоялось очень приятное маленькое научное собрание. Сейчас Какутани преподает в Соединенных Штатах, а Стоун и Эрдеш вернулись в Европу.

^* (Остров в Атлантическом океане у побережья Северной Америки, на котором расположена восточная часть Нью-Йорка.)

В конце лета Ингам, как он и рассчитывал, возвратился в Англию, а его жена, дети и девушка, помогавшая по хозяйству, провели с нами еще целый год. Мы снова совершали вместе длинные прогулки, которые теперь казались детям уже не такими трудными. Я несколько раз навещал Ингамов после того, как они все вернулись в Англию. Один из мальчиков, если я не ошибаюсь, готовится сейчас поступить в университет, другой стал офицером военно-воздушных сил. Они до сих пор любят Нью-Хемпшир и нашу долину.

Винтнер по-прежнему оставался нашим летним соседом. Мы решили в 1940/41 учебном году поработать вместе, и он ради этого приехал в Кембридж. К несчастью, в тот год военная тематика поглощала все мое внимание. Я понимал, что, нарушая наш неофициальный договор, я поступаю в какой-то степени нечестно по отношению к Винтнеру. Но оказалось, что он в состоянии игнорировать тягостность политической напряженности, а я нет. И хотя я охотно уделял нашей совместной работе часть своего времени, я не мог сосредоточить на ней все свои интересы. Так мы и шли двумя разными дорогами, постепенно уходя все дальше и дальше друг от друга.

Весной разразилась катастрофа в Норвегии, катастрофы во Франции ждали со дня на день. Душевный покой, который приносила нам жизнь в Нью-Хемпшире, куда мы убегали от потрясений внешнего мира, ничего не стоил перед лицом близящейся гибели европейской цивилизации. В августе 1940 года в Дартмуте состоялся летний съезд Американского математического общества. Он был настолько приятным, насколько мог быть приятным съезд, во время которого всех по-настоящему интересовала только война.

Так как в технике связи приходится производить много сложных вычислений с коплексными числами, сотрудники Телефонной компании Белла построили специальный прибор - цифровую вычислительную машину, выполняющую всевозможные расчеты. При этом они воспользовались одним очень важным нововведением. Дело в том, что обычная арабская цифровая система придает специальное значение числу 10, оправданное только привычкой и не находящее никакого подтверждения в основных законах арифметики. Вместо того чтобы записывать каждое число в виде суммы стольких-то единиц, стольких-то десятков, стольких-то сотен и т. д., мы можем с тем же правом представить целое число в виде суммы единиц, двоек, четверок, восьмерок и т. д. В этом случае вместо десяти цифр, используемых в обычной арифметике, нам понадобятся только две цифры, а именно нуль и единица.

Русские крестьяне при арифметических расчетах в какой-то мере использовали такое представление чисел, называемое двоичной системой счисления^*. Большое преимущество этой системы перед обыкновенной состоит в том, что таблица умножения сводится здесь к единственному утверждению, что 1×1 = 1.

^* ( На самом деле сведение произвольных умножений к последовательности удвоений, сложений и вычитаний, а произвольных делений - к последовательности делений пополам, сложений и вычитаний, эквивалентное в какой-то степени использованию двоичной системы счисления, до начала XX века было очень распространено в народной арифметике целого ряда европейских и азиатских стран, а не только России. (Прим. ред.))

Нетрудно понять, что механизировать арифметические расчеты, выполняющиеся в двоичной системе счисления, значительно легче, чем обычные вычисления над числами, записанными в десятичной системе счисления. Это и было учтено в машине Лаборатории Белла, использующей двоичную запись чисел. Единственным серьезным недостатком такой машины является то, что во всех остальных случаях люди все-таки пользуются десятичной системой и встречающиеся числовые данные всегда представляются в виде десятичных чисел. Тем не менее в тех случаях, когда приходится выполнять много громоздких вычислений, часто бывает выгодно пренебречь этим обстоятельством и перевести все исходные данные в двоичную систему, а все окончательные результаты - обратно в десятичную. В технике двоичная система счисления иногда используется при измерении толщины механических деталей с помощью специального набора "эталонов толщины". Предположим, что у нас имеется один эталон толщиной точно в один дюйм, один эталон толщиной в два дюйма, один эталон толщиной в четыре дюйма и один - толщиной в восемь дюймов. Тогда, комбинируя эти эталоны, мы можем получить любые толщины, равные целому числу дюймов от одного до пятнадцати включительно. Для этого надо только ставить наши эталоны друг на друга в следующих комбинациях:

1 дюйм - эталон в 1 дюйм,

2 дюйма - эталон в 2 дюйма,

3 дюйма - эталон в 2 дюйма и эталон в 1 дюйм,

4 дюйма - эталон в 4 дюйма,

5 дюймов - эталон в 4 дюйма и эталон в 1 дюйм,

6 дюймов - эталон в 4 дюйма и эталон в 2 дюйма,

7 дюймов - эталон в 4 дюйма, эталон в 2 дюйма и эталон в 1 дюйм,

8 дюймов - эталон в 8 дюймов,

9 дюймов - эталон в 8 дюймов и эталон в 1 дюйм,

10 дюймов - эталон в 8 дюймов и эталон в 2 дюйма,

11 дюймов - эталон в 8 дюймов, эталон в 2 дюйма и эталон в 1 дюйм,

12 дюймов - эталон в 8 дюймов и эталон в 4 дюйма,

13 дюймов - эталон в 8 дюймов, эталон в 4 дюйма и эталон в 1 дюйм,

14 дюймов - эталон в 8 дюймов, эталон в 4 дюйма и эталон в 2 дюйма,

15 дюймов - эталон в 8 дюймов, эталон в 4 дюйма, эталон в 2 дюйма и эталон в 1 дюйм.

Это представление толщины с помощью наборов эталонов эквивалентно записи чисел от 1 до 15 в виде следующих совокупностей единиц и нулей: 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110 и 1111, Я не помню, до или после собрания в Дартмуте Венивар Буш разослал преподавателям МТИ опросный лист, чтобы собрать предложения о наилучшем использовании ученых в случае вступления США в войну. Я придерживался в этом вопросе совершенно определенного мнения и был твердо убежден в необходимости научного сотрудничества, которое помогло бы преодолеть барьеры между различными науками и в то же время было бы добровольным, сохраняя за учеными значительную долю инициативы и личной ответственности. Я не питал никакого доверия к планам, осуществление которых требовало почти полного подчинения отдельной личности вышестоящим инстанциям, пользующимся непререкаемым авторитетом и неизбежно ограничивающим работу каждого человека узкими рамками. Поэтому я предлагал такую систему организации, при которой небольшие мобильные объединения ученых, работающих в различных областях, трудятся над разрешением определенного круга проблем. Я предполагал, что, добившись каких-то конкретных результатов, объединение сможет передать их специальной руководящей "группе внедрения" и, обогатившись новыми научными сведениями и опытом совместной работы, в полном составе перейдет к разрешению следующей задачи.

Из всего этого ничего не вышло. Люди, привыкшие работать почти исключительно с помощью различных механических приспособлений, обычно проникаются к ним не-умеренной любовью, в значительной мере вызванной тем, что механизмы не подвластны капризам, свойственным человеческим существам.

Механизация легко становится чем-то вроде религии. К счастью, перипетии последних двадцати лет у многих, в том числе и у Буша, поколебали веру в беспредельные возможности машины. Однако осталось еще достаточно людей, которые не успели так близко, как Буш, познакомиться со всеми недостатками и достоинствами машин и, следуя моде, предпочитали большие лаборатории и авторитетную администрацию.

Возвращаясь с собрания Математического общества, я обсуждал с Левинсоном - как ученый он уже прочно стоял на собственных ногах - общие проблемы устройства счетных машин, поскольку я подумывал о том, чтобы избрать эту область своей военной специальностью.

В течение некоторого времени я по просьбе Буша занимался поисками путей использования счетных машин для решения дифференциальных уравнений в частных производных, и у меня создалось впечатление, что наиболее подходящим средством механизации их решения может быть техника сканирования, применяемая в телевидении.

Опыт работы со счетными машинами, основанными на двоичной системе счисления, убедил меня, что электронная двоичная машина как раз и может служить устройством, осуществляющим быстрые вычисления, требующиеся при решении задач, описываемых уравнениями в частных производных.

Я совершенно отчетливо представлял себе, что машина, способная решать уравнения в частных производных, должна производить немыслимо большое количество операций в немыслимо короткое время. Отсюда следовало, что будущее быстродействующих вычислительных машин, предназначенных для таких целей, не могло основываться на развитии моделей Буша, в которых физические величины представлялись электрическими токами или какими-либо переменными механическими параметрами самой машины, а скорее требовало какого-то чудодейственного усовершенствования обыкновенного электрического арифмометра, использующего, как я уже говорил, двоичную систему счисления вместо десятичной.

Теперь, когда я всерьез заинтересовался вопросами, связанными со скоростью вычислений, мне пришлось рассмотреть относительные достоинства двух основных стратегий вычислительной техники. Одна из этих стратегий, которой придерживался Буш, получила название техники аналоговых устройств и заключалась в том, что числам, участвовавшим в вычислениях, сопоставлялись какие-то измеримые физические величины, имеющие значение, равное соответствующему числу. Другой, цифровой метод вычислительной техники, который используется, например, в обычных настольных арифмометрах, исходит из представления каждого числа в виде определенной последовательности цифр.

Существенным различием между аналоговыми и цифровыми вычислительными машинами является то, что только цифровая машина в принципе работает так же, как и мы сами, когда решаем задачу с помощью карандаша и бумаги. Изображая некоторое число символом 56, мы имеем в виду, что оно является суммой пяти десятков и шести единиц. Если нам нужно умножить это число на 38, т. е. на сумму трех десятков и восьми единиц, мы выполняем эту операцию в таком порядке, как это показано ниже:

При этом нам ни разу не пришлось воспользоваться чем-либо выходящим за рамки таблицы умножения и простейших правил сложения или вспоминать, что наши числа 56 и 38 - это на самом деле 56 градусов или 38 дюймов.

Однако существуют такие цифровые вычислительные машины, в которых число 10 не играет никакой особенной роли и которые работают, исходя из двоичной системы счисления. Для того чтобы понять, как это делается, рассмотрим, например, умножение 7 × 5 = 35 и представим числа 7 и 5 в виде

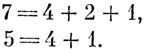
Согласно приведенным равенствам в двоичной системе счисления число 7 изображается числом 111, число 5 - числом 101 (это и значит, что 7 равно сумме одной четверки, одной двойки и одной единицы, а 5 - сумме одной четверки, нуля двоек и одной единицы). При выполнении операции умножения этих двух чисел мы поступим теперь следующим образом:

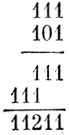
Вспомнив далее, что в двоичной системе счисления 2 = 10, мы можем переписать число 11211 в виде 12011, или в виде 20011, или, наконец, в виде 100011. Лишь последняя форма является истинно двоичной, ибо только в ней не используются никакие другие цифры, кроме 0 и 1. Переходя теперь обратно к десятичной системе счисления, получим: 5×7 = 1·32 + 0·16 + 0·8 + 0·4 + 1·2 +1 = 35. Этот метод получил название метода умножения в двоичной системе счисления. Я хочу подчеркнуть еще раз, что по существу он ничем не отличается от обычного метода умножения, использующего десятичную систему счисления.

Принцип действия аналоговых вычислительных устройств является совсем другим: здесь за основу может быть, например, принято то, что в электродинамометре две катушки притягиваются друг к другу с силой, пропорциональной произведению сил протекающих по ним токов, и что эта сила притяжения может быть измерена, если снабдить прибор специальной шкалой. Поэтому, если по обмотке одной катушки течет ток в семь единиц, а другой - в пять единиц, то показание прибора в соответствующих единицах будет равно 35. Приборы такого типа, используемые для перемножения чисел, получили название аналоговых в связи с тем, что они заменяют первоначальную ситуацию, в которой было необходимо умножить одну какую-то величину на другую, новой ситуацией, в которой роль этих величин играют уже две силы тока, причем токи эти ведут себя аналогично исходным величинам, т. е. должны перемножаться менаду собой для определения величины некоторого физического эффекта.

Цифровые вычислительные машины отличаются от аналоговых, в частности, тем, что они в принципе позволяют получить ответ с любой степенью точности, определяемой лишь точностью задания исходных данных, в то время как точность аналоговых устройств ограничена той точностью, с которой исходная ситуация оказывается аналогичной некоторой другой, используемой в качестве модели в наших вычислениях. Типичными аналоговыми устройствами были, например, машины Буша, предназначенные для решения дифференциальных уравнений.

Что же касается относительных достоинств вычислительных машин этих двух типов, то разнообразие и гибкость современных электрических и прочих измерительных приборов позволяют в настоящее время построить достаточно хорошую аналоговую машину с меньшими затратами труда и времени, чем надо для создания цифровой машины такого же качества. Однако если нам нужны большая скорость или высокая точность вычислений, то все преимущества оказываются на стороне цифровых машин. Только некоторые исключительные по своим качествам физические приборы могут обеспечить точность, превышающую одну десятитысячную часть измеряемой величины, что соответствует всего лишь точности, получаемой при использовании четырех десятичных разрядов или менее четырнадцати двоичных разрядов в цифровой машине.

Кроме того, физические измерения с такой степенью точности вряд ли могут оказаться очень быстрыми. Аналоговые устройства принципиально не способны обеспечить скорость вычислений, достаточную для проведения наиболее точных и сложных из тех расчетов, необходимость в которых возникает в современной науке и технике. Поэтому мне кажется, что наивысший расцвет использования устройств такого рода сейчас уже позади.

Что же касается цифровых машин, то мне пришлось углубиться в изучение самих принципов их работы. В обычном настольном арифмометре принцип работы заключается в том, что в зависимости от положения одних колес определяется положение некоторых других. Каждое из таких положений выбирается из числа десяти возможных, отличающихся величиной угла поворота относительно некоторого "начального положения". Эти десять положений нетрудно задать с помощью десяти зубцов. Однако при использовании металлических колес мы сталкиваемся со сложными проблемами преодоления инерции и сил трения, существенно ограничивающих возможности наших машин.

Со всех точек зрения казалось желательным заменить механическую систему выбора, осуществляемую в старых цифровых машинах, электронной. Можно было ожидать, что в результате такой замены новые машины окажутся по крайней мере в двух отношениях более совершенными, чем старые. Во-первых, инерция потока электронов значительно меньше инерции любой механической системы, и, во-вторых, в электрических цепях технически гораздо легче с помощью усилителей бороться с потерями энергии, вызываемыми процессами типа трения (например, выделением тепла в сопротивлениях). По этим причинам я был абсолютно уверен в том, что быстродействующие вычислительные машины недалекого будущего будут электронными и цифровыми. Надо, однако, сказать, что в то время такие идеи стали уже довольно часто встречаться в научной литературе, так что здесь моя точка зрения была лишь одним из проявлений духа эпохи.

Как я уже сказал, в десятичных цифровых машинах в качестве основной логической операции используется выбор из десяти различных возможностей, в то время как в двоичной машине такую же роль играет выбор из двух возможностей. Повсеместное использование десятичной системы счисления, по-видимому, объясняется просто тем, что десять - это число пальцев на наших руках. Некоторые народности, например индейцы майя, вероятно, использовали для счета пальцы рук и ног и поэтому пришли К двадцатеричной системе счисления. Любопытно отметить, что если бы люди не отличались от героев забавных рисунков Уолта Диснея, т. е. имели бы всего по четыре пальца на каждой руке, то, по-видимому, у пас была бы распространена восьмеричная система счисления, лишь незначительно отличающаяся от двоичной (так как 8 = 2×2×2).

Тем не менее можно считать, что нам повезло, так как десятичная система счисления хотя и не является самой удобной, но все же много удобнее, чем, скажем, тринадцатеричная. В самом деле, в вычислительных машинах, основанных на десятичной системе, используются колеса с десятью зубцами, расположенными на одинаковых рас-стояниях друг от друга. Для создания таких колес надо уметь строить правильные десятиугольники, т. е. правильные многоугольники с десятью вершинами. Эта задача планиметрии неизмеримо более проста, чем задача построения правильного многоугольника с тринадцатью сторонами.

Однако при использовании электронных схем устройства, заменяющие колеса в механических счетных машинах, не зависят уже от законов планиметрия и здесь выбор из десяти равноправных возможностей моделируется не так легко. Наиболее естественным в электронных схемах оказался выбор одного из двух возможных исходов.

Схемы с двумя различными состояниями устойчивого равновесия были известны уже давно и получили название триггерных. Единственная возможность для построения схемы с десятью различными состояниями заключается, по-видимому, в использовании комбинации из нескольких таких триггерных схем. По самому принципу работы триггера число различных состояний сложной триггерной схемы определяется числом различных комбинаций состояний каждого из триггеров, и это число должно быть степенью двух. Поэтому естественный способ построения схемы с десятью устойчивыми состояниями заключается в использовании схемы с шестнадцатью состояниями, шесть из которых не употребляются.

Однако при конструировании машины нам приходится затрачивать усилия и деньги не только на то, что машина будет делать, но и на все то, что эта машина могла бы делать; поэтому, используя лишь десять состояний из шестнадцати возможных, мы вынуждены будем расходовать на 37¹/₂% больше того, что в действительности необходимо. По этим причинам я считал, что быстродействующая машина для решения дифференциальных уравнений в частных производных должна быть двоичной цифровой электронной машиной.

Для того чтобы работать в двоичной системе счисления, нужно иметь машины, которые осуществляют выбор одной из двух возможностей, таких, как, например, наличие или отсутствие отверстия в кусочке картона - перфорационной карте. Устройство этого типа уже в то время использовалось в машинах "Холлерит", выпускавшихся фирмой ИБМ^*.

^* ( ИБМ(ШМ)-сокращенное "International Business Machines" ("Международные деловые машины")-название самой известной американской фирмы, занимающейся производством счетных машин.)

Однако такой метод физического представления чисел в двоичной системе счисления непригоден для действительно быстродействующей вычислительной машины. Пробивание отверстий в перфокарте - очень медленная операция в масштабах времени, где за единицу берется продолжительность одной операции порядка миллионных долей секунды. А именно такого порядка продолжительности операции надо достичь, чтобы можно было утверждать, что наша машина действительно быстродействующая. Кроме того, при сложных вычислениях число уже использованных перфокарт, от которых нам нужно теперь как-то избавиться, и число новых перфокарт, которыми нужно запастись на будущее, очень скоро стало бы астрономическим.

Разумеется, скорость пробивки отверстий можно значительно повысить, заменив механический перфоратор устройством, в котором для этой цели используется электрический разряд, однако задача хранения и использования огромных масс карточек при этом нисколько не упростится. Поэтому естественно было прийти к мысли об использовании металлической ленты с магнитными отметками, наносимыми электромагнитом. Такие отметки можно считывать с высокой скоростью и с такой же скоростью стирать их, после чего лента становится пригодной для повторного использования.

Одна из основных задач, связанных с использованием таких лент, заключается в том, что размеры отметок нужно делать как можно меньшими, с тем чтобы на данной площади можно было разместить как можно больше четко различимых отметок. А для этого необходимо использовать записывающие и считывающие магнитные головки с исключительно малыми размерами полюсов. В то же время мне казалось, что уменьшение размеров полюсов магнитных головок не приведет к желаемому результату вследствие распространения магнитного поля вдоль ленты, если только сама лента или по крайней мере ее эффективный магнитный слой не будут чрезвычайно тонкими.

В результате, частично в качестве вывода из собственных размышлений, частично под влиянием совместного обсуждения этих вопросов с моими коллегами, хорошо знакомыми с техническими новинками в этой области, у меня возникла идея о том, что задачи обеспечения двух основных требований, предъявляемых к магнитной ленте, - прочности и возможности намагничивания - нужно решать по отдельности. А именно, следует выбрать какой-либо достаточно прочный немагнитный металл, на который наносится тонкий магнитный слой. В то время я больше всего думал о тонком слое железа, нанесенном на ленту из меди или какого-нибудь другого немагнитного металла, но по совету кого-то из моих коллег я подумывал также о ленте, которая в настоящее время получила самое широкое распространение, - о бумажной ленте, покрытой тонким слоем магнитной окиси железа.

Недавно я разговаривал с одним из моих знакомых, работающих в фирме ИБМ, о современных быстродействующих вычислительных машинах и, в частности, о машинах, использующихся для решения дифференциальных уравнений в частных производных при помощи метода, получившего теперь название метода Монте-Карло и основанного на использовании многократно повторяющегося процесса осреднения. У меня создалось впечатление, что системы, о которых я думал в 1940 году, принципиально ничем не отличались от того, что сейчас реально используется.

Шансы сторон в большом игорном доме в высшей степени постоянны и предсказуемы, и метод Монте-Карло как раз и состоит в том, что математическая задача формулируется как задача о некоторой идеальной игре, после чего игра эта многократно разыгрывается и определяется достигнутый выигрыш. Вычислительное устройство, предложенное мною в 1940 году, как и метод Монте-Карло, не основывалось на достижении некоторого состояния равновесия, а также было связано с определением исходов ряда идеальных игр.

Я послал отчет о моих соображениях по этому вопросу Венивару Бушу, но этот отчет был встречен без особого энтузиазма. Буш признал, что в предложенном мной подходе содержатся некоторые возможности, но он считал, что это дело далекого будущего, не имеющее никакого отношения ко второй мировой войне. Он посоветовал мне вернуться к этому вопросу после войны, а сейчас сосредоточиться на более насущных проблемах.

Впоследствии я узнал, что он не был особенно высокого мнения о моем предложении в первую очередь потому, что я не был инженером и никогда не собрал ни одной схемы. Буш весьма низко оценивал любую работу, еще не получившую физического воплощения. Сейчас единственным утешением для меня может служить лишь мысль, что я подошел к правильному решению чуть ли не на десять лет раньше создания технических методов, доказавших справедливость моих идей. Выяснив, что проблема создания совершенной вычислительной техники не является той, в которой я легче всего могу быстро принести пользу, я стал осматриваться в поисках такой области, в которой моя работа в условиях надвигающейся войны была бы более полезной. Одно время у меня появились мысли о математических и практических аспектах проблемы кодирования и декодирования сообщений. Мои идеи в этой области позволяли создать некоторые новые методы кодирования и декодирования, но этого было еще недостаточно, чтобы оправдать их дальнейшую разработку. В самом деле, для того чтобы иметь практическую ценность, новые методы должны были оказаться значительно лучшими, чем все реально используемые или не используемые, но легко изобретаемые методы.

Вопрос о том, какое из двух кодирующих-декодирующих устройств является лучшим, совсем не прост. Можно с уверенностью утверждать, что любой достаточно большой кусок зашифрованного текста всегда может быть расшифрован, если только противник располагает достаточным временем. С другой стороны, нужно учитывать, что задача дешифровки зашифрованного текста не обязательно является тривиальной, даже если код известен заранее. В хорошем шифре должны сочетаться простота и автоматичность дешифровки для лица, знающего шифр, с большими трудностями его дешифровки тем, кто этого шифра не знает.

Как это обычно бывает, когда системе предъявляются два противоречивых требования, одной наилучшей системы шифровки не существует, а есть целый ряд оптимальных систем, отличающихся друг от друга тем, какое значение придается одному из этих требований по сравнению с другим. Так, например, существуют несложные шифры, используемые при передаче сообщений, которые должны оставаться секретными лишь в течение нескольких часов, и гораздо более сложные шифры для сообщений, которые должны оставаться секретными целые месяцы. Между этими двумя крайними случаями располагается множество промежуточных шифров. Поэтому нельзя разрабатывать новые шифры с академических позиций, не зная уже сложившихся традиций и практических требований, предъявляемых к ним в каждом частном случае. Таким образом, мне снова пришлось отказаться от продолжения начатых исследований и заняться поиском еще одной возможной области приложения моих способностей. Такую область я нашел в задачах о конструировании систем управления огнем противовоздушной артиллерии.

Когда я был еще мальчиком, проблема управления огнем ставилась только для береговых батарей, обстреливающих приближающиеся военные корабли противника, т. е. для орудий, стреляющих по цели, движущейся настолько медленно, что с помощью самых примитивных счетных устройств типа специальных таблиц удавалось выполнить все нужные для наводки орудия вычисления прежде, чем цель выходила за пределы эффективного огня батареи.

Появление самолетов в ходе первой мировой войны в корне изменило такое положение вещей. Задача управления огнем противовоздушной артиллерии совсем не похожа на задачу артиллерийского обстрела крепости, а скорее напоминает охоту на уток. Пока вы стреляете, утка не остается на месте, и если целиться в ту точку, в которой утка находится в момент выстрела, то, когда прилетит пуля, она окажется уже далеко. Поэтому нужно стрелять с определенным упреждением и уметь оценивать величину этого упреждения быстро и точно. Если такая оценка окажется неверной, то вам, наверное, не удастся выстрелить по этой же утке еще раз.

По тем же причинам в систему управления огнем противовоздушной артиллерии приходится вводить что-то эквивалентное таблице поправок, позволяющей автоматически определять необходимое упреждение для орудия, с тем чтобы самолет и снаряд оказывались в одной и той же точке одновременно. Задача об этих поправках па первый взгляд может казаться чисто геометрической, но при более тщательном подходе к ее решению выясняется, что оно сопряжено с необходимостью как можно более точной оценки будущего положения самолета по данным наблюдений его положения в прошлом. Задача предсказания будущего положения самолета сводится при этом к тому, что математики называют проблемой экстраполяции.

Еще раньше в работе над некоторыми электротехническими задачами я познакомился с теорией операторов - устройств, преобразующих некоторый электрический сигнал, поступающий на вход устройства, в какой-то сигнал на выходе. С математической точки зрения оператор может быть описан формулой, задающей преобразование одного сигнала в другой, причем не всем возможным формулам такого рода соответствуют операторы, которые можно реализовать на практике. Основное условие физической реализуемости операторов сводится к тому, что выходной сигнал системы должен определяться лишь значениями входного сигнала в прошлом и в настоящем. Решение задачи о стрельбе по самолету связано с необходимостью приближенного представления с помощью физически реализуемого оператора операции перехода от прошлого к будущему положению цели. Эта операция строго выражается оператором, физически не реализуемым. В самом деле, только пророк, знающий, что творится в голове пилота, может абсолютно точно предсказать положение самолета в будущем. Однако на практике мы очень часто располагаем достаточными средствами для выполнения менее сложной задачи - приближенного прогнозирования будущего положения самолета с удовлетворяющей нас точностью.

Математическое решение проблемы прогнозирования, напрашивавшееся с самого начала, было практически непригодным, так как фактически предполагало, что у нас есть информация и о будущем поведении самолета. Тем не менее я смог показать, что это решение может быть приближено оператором, свободным от этого недостатка.

Я не хочу углубляться здесь в технические подробности, доступные лишь инженерам и ученым. Достаточно сказать, что я исследовал возможности приближенной замены физически не реализуемых операторов операторами, физически реализуемыми. Я изложил свои взгляды профессору Колдуэллу, который до войны руководил работами над вычислительными машинами Буша в МТИ, а теперь должен был заниматься применениями этих машин в военном деле. В соответствии с существовавшими в то время обычаями Колдуэлл немедленно объявил мою работу секретной, так что после этого я уже не мог открыто излагать свои идеи всем, кому я хотел.

Для проверки полученных мною результатов мы с Колдуэллом решили применить дифференциальный анализатор Буша, воспользовавшись тем, что из его частей с легкостью можно собрать много новых приборов для решения самых различных задач. С этой точки зрения дифференциальный анализатор напоминал большой радиотехнический конструктор. И в самом деле, когда англичане решили пойти по стопам Буша и построить свой дифференциальный анализатор, они воспользовались деталями, взятыми из обычных детских конструкторов, и добились вполне удовлетворительных результатов.

Мы провели несколько опытов с различными схемами обработки и обнаружили, что те методы, которые мы заранее считали лучшими, оказались лучшими и на практике. Наши приборы представляли собой ряд сумматоров, множительных устройств в механических интеграторов.

На этом этапе разработка теории прогнозирования стала правительственным заданием и к работе был привлечен молодой инженер Джулиан Байглоу, уже работавший в течение некоторого времени в фирме ИБМ. Так было положено начало нашему длительному сотрудничеству. Байглоу - тихий, прекрасно воспитанный человек, выходец из Новой Англии. Единственный его научный порок - это преизбыток научных добродетелей. Он всегда стремится к идеальному, и еще ни одна работа в его глазах не выглядела достаточно завершенной.

Раньше он был энтузиастом любительской авиации, но во время войны этот вид спорта, если и не стал совсем недоступным, то, во всяком случае, оказался слишком дорогим для рядового любителя. В практике пилотов-любителей аварии, как правило, бывают не слишком серьезными в том смысле, что чаще всего пилоту удается избежать тяжелых повреждений. Но для самолета не существует незначительных аварий. Ремонт самолета всегда производится квалифицированными механиками, и качество его проверяется официальными представителями Управления гражданской авиации. Поскольку аварии обычно происходят в самых отдаленных местах страны, ликвидация их последствий требует очень значительных затрат.

На несколько лет Байглоу переключился на выхаживание безнадежно старых и дряхлых автомобилей. Для обычного автомобилиста машина является просто средством передвижения, позволяющим ему добираться туда, куда хочется, но для истинного любителя каждая новая машина - это вызов его способностям к преодолению трудностей. Инженер такого типа никогда не удовлетворится обычной машиной. Либо он постарается сделать свою машину лучшей в мире, либо употребит всю свою изобретательность для того, чтобы заставить работать машину, место которой уже давно на свалке металлолома. Если вы пускаетесь в путь с таким любителем за рулем, то можете не опасаться никаких серьезных происшествий, но без приключений вам никогда не обойтись. Помню, однажды фон Нейман хотел поговорить с Байглоу, которым он интересовался как одним из возможных участников работы по созданию быстродействующих вычислительных машин. Из Принстона мы позвонили в Нью-Йорк, и Байглоу согласился приехать к нам на своей машине. Мы подождали до назначенного часа, но Байглоу не появился; не приехал он и еще через час. И только потеряв всякую надежду, мы услышали пыхтение древней машины. Это Байглоу, наконец, добрался к нам буквально на последнем такте мотора машины, которая в других руках остановилась бы уже много месяцев тому назад.

Мы с Байглоу вначале попытались определить границы применимости нашего метода прогнозирования, так как заранее почти с полной уверенностью можно было предположить, что возможности этого метода довольно ограничены. На этот раз, вместо того чтобы испытывать нашу систему прогнозирования на гладких кривых, мы решили испытать ее на кривой, состоящей из двух прямых, образующих угол.

Следует сказать, что прибор для прогнозирования состоял из двух блоков, одного, который все время следил за данной кривой, и другого, который на основе полученной информации о поведении кривой в прошлом устанавливал, как будет выглядеть эта кривая через некоторое время в будущем. Когда мы испытывали прибор не на гладкой кривой, а на кривой, в которой за одним отрезком прямой следует другой, наклоненный под определенным углом к первому, мы обнаружили, что система по-прежнему работает, но чрезвычайно странным образом.

Удивительным, волнующим и, по правде говоря, неожиданным было то, что прибор, сконструированный для наилучшего слежения за гладкой кривой, оказался слишком чувствительным для угловых точек. При переходе через такую точку в нем возникали сильнейшие автоколебания. Мы несколько раз исследовали это явление и каждый раз получали одни и те же результаты. Отсюда было уже недалеко до мысли о том, что встретившееся нам явление находится в порядке вещей и никак не может быть изменено. Но это значит, что в самой природе процесса прогнозирования заложено то, что приборы, рассчитанные на точное слежение за гладкими кривыми, оказываются чрезмерно чувствительными в применении к ломаным. По-видимому, здесь мы еще раз сталкиваемся с тем же противодействием природы, которое проявляется в принципе неопределенности Гейзенберга, согласно которому нельзя одновременно точно определить, где находится частица и с какой скоростью она при этом движется.

Чем больше мы изучали возникшую задачу, тем больше убеждались в том, что мы правы и что встретившаяся нам трудность является принципиальной. Но если уж мы не могли достигнуть того, к чему стремились (впрочем, без особой надежды на удачу), т. е. построить идеальную систему прогнозирования, годную во всех случаях, нам оставалось по одежке протягивать ножки и попытаться разработать такую систему прогнозирования, которая была бы наилучшей среди всех, не противоречащих законам математики. При этом было необходимо ответить на один важный вопрос: что следует понимать под наилучшей системой прогнозирования? Уменьшение ошибки слежения за гладкой кривой ведет к увеличению ошибок, связанных с излишней чувствительностью следящей системы при слежении за ломаной. Чем же следует руководствоваться в поисках компромисса между ошибками этих двух -типов?

Ответ на этот вопрос заключается в том, что при выработке разумного компромисса можно руководствоваться только статистическими представлениями. Зная статистическое распределение кривых, которые нам надо экстраполировать, т. е., например, зная статистическое распределение путей самолетов, по которым ведется стрельба, можно искать такой метод прогнозирования, при котором некоторая величина, характеризующая ошибку, принимает наименьшее значение. Наиболее естественной величиной, с которой мы и начали (руководствуясь в первую очередь надеждой на простоту соответствующих расчетов, а не на то, что полученные при этом результаты будут иметь особенно большое военное значение), является средний квадрат ошибки прогнозирования. Иначе говоря, мы каждый раз определяли квадрат ошибки прогнозирования (т. е. квадрат разности между истинным и предсказанным значениями координаты кривой), а затем подсчитывали среднее значение этой величины за все время работы нашего прибора, которое и старались минимизировать. При этом мы смогли сформулировать задачу прогнозирования как некоторую задачу о нахождении минимума, т. е. придать ей определенную математическую форму, зависящую, разумеется, от предположений о свойствах статистической совокупности кривых, которые нам придется экстраполировать. Область математики, посвященная решению задачи о нахождении минимума величин, зависящих от вида некоторых кривых, известна под названием вариационного исчисления и представляет собой специальную математическую дисциплину, имеющую многочисленные применения. В наиболее обычных случаях задачи вариационного исчисления сводятся к некоторым дифференциальным уравнениям, определяющим функции или кривые, удовлетворяющие требуемым условиям минимума; однако в ряде случаев (с одним из которых как раз нам и пришлось встретиться) они приводят к родственным уравнениям другого типа, называемым в математике интегральными.

К счастью, я уже занимался теорией интегральных уравнений и раньше, но еще более удачным оказалось то, что уравнения, к которым привело нас решение задачи прогнозирования, представляли собой лишь немного более общий случай уравнений, ранее изученных Эберхардом Хопфом и мною. Таким образом, я смог не только поставить задачу прогнозирования, но и решить ее. В довершение всех удач полученное решение было по форме довольно простым. Оказалось, что решение, найденное нами на бумаге, нетрудно воплотить в конкретный прибор; для этого нужно было только собрать несложную схему из индуктивностей, емкостей и сопротивлений и подключить ее к небольшому электродвигателю того типа, который можно купить у любой фирмы, выпускающей измерительные приборы.

Мы построили прибор, преобразовывавший высоту движущейся точки в электрическое напряжение. Затем мы пропускали это изменяющееся во времени напряжение через совокупность сопротивлений, конденсаторов и катушек с магнитными сердечниками. В другой точке системы мы снимали напряжение и непрерывно измеряли его вольтметром. Конкретный тип вольтметра, использовавшегося нами, позволял строить непрерывный график изменения напряжения. Эта запись использовалась в качестве выходного сигнала и служила для прогнозирования значения напряжения на некоторый интервал времени вперед.

Следующая задача, которой я занялся, состояла в прогнозировании на основании неточных данных о прошлом. Эта задача также сводилась к задаче на нахождение минимума, причем здесь уже нам надо было располагать не только статистикой самих упреждаемых кривых, но и статистикой ошибок в определении прошлых координат этих кривых. После этого рассматриваемая задача о нахождении минимума свелась к другому уравнению Винера - Хопфа, решаемому при помощи тех же методов. Таким образом, и здесь удалось построить вполне удовлетворительную математическую теорию.

В науке часто недостаточно решить какую-нибудь задачу или группу задач. После этого нужно присмотреться к этим задачам и заново осмыслить, какие же задачи вы решили. Нередко, решая одну задачу, мы автоматически находим ответ и на другой вопрос, о котором раньше вовсе не думали.

Именно так обстояло дело с новой теорией прогнозирования. Оказалось, что в теории прогнозирования будущих значений полезного сигнала, наблюдаемого в смеси с шумами, на основе данных о статистических характеристиках полезного сигнала и шума содержится также и основная идея нового подхода к задаче о таком разделении полезных сигналов и шумов, которое можно было бы считать наилучшим.

Мы обнаружили это в самое подходящее время, когда только что появившаяся новая техника радиолокации встретилась с серьезными трудностями. При использовании радиолокаторов было крайне важно уметь обнаруживать слабые сигналы на фоне маскирующего сигнал шума. Для инженера-электрика шум - это отнюдь не только те звуки, которые можно услышать но и любое нежелательное электрическое возмущение. Например, шумом являются мерцание и мелькание изображения в плохо настроенном телевизоре. Шумами называются и все те сигналы, которые проходят через радиолокационную систему и вместо того, чтобы уточнять характер полезного сигнала, лишь искажают его.

Отделение полезного сигнала от шума осуществляется при помощи фильтра. Электрические фильтры известны давно и уже много лет назад начали использоваться в телефонии, для того чтобы очищать полезный сигнал от сопутствующих ему шумов. Первоначально они конструировались так, чтобы пропускать все сигналы из определенного диапазона частот, практически не изменяя их интенсивности, и как можно сильнее ослаблять сигналы с частотами, лежащими вблизи указанного диапазона, но все же выходящими из него.

Когда же на основании опыта телефонных фильтров были созданы фильтры для телевизионных установок, оказалось, что, начиная с некоторого момента, чем лучше становились характеристики фильтра, тем хуже он работал в телевизионной схеме. В чем же здесь дело? Ответ заключается в том, что телефонные фильтры были рассчитаны на специальные характеристики человеческого уха. Ухо человека представляет собой весьма чувствительный прибор для определения высоты звука, оно достаточно точно оценивает его громкость и очень мало реагирует на так называемые фазовые соотношения, другими словами, лишь очень грубо регистрирует те моменты времени, когда колебания воздуха проходят через нуль. Переменный же ток, как я уже говорил, характеризуется не одной величиной, определяющей его интенсивность, а сразу двумя величинами, определяющими его интенсивность и фазу. Рисунок, изображающий переменный ток, можно сравнить с плоским гребнем. Перемещая такой гребень взад и вперед в его плоскости, я меняю определенную величину, которую и называют фазой. В акустике такие изменения фазы не являются совершенно неосязаемыми, но роль их очень невелика, и поэтому первоначальные телефонные фильтры и другие фильтры для звуковых колебаний обычно строились без всякого учета возможных изменений фазы.

Радиолокатор же, так же как и телевизор, порождает сигналы, воспринимаемые глазом, и для класса сообщений, передаваемых по телевидению или содержащихся в сигнале радиолокатора, глаз ничуть не менее чувствителен к ошибкам в значении фазы, чем к ошибкам в значении амплитуды. Таким образом, при использовании обычных телефонных фильтров в радиолокации и телевидении свойственные этим фильтрам фазовые искажения оказались слишком дорогой ценой за отличное качество передачи амплитуды в широком диапазоне частот. Для того чтобы свести к минимуму суммарную ошибку в телевидении и радиолокации, необходимо было за счет некоторого увеличения амплитудных искажений по сравнению с возможностями лучших телефонных фильтров существенно уменьшить фазовые искажения. Для определения разумного компромисса между этими двумя типами искажений предложенный мною метод хотя и не являлся идеальным, но все же оказался вполне полезным и давал лучшие результаты, чем все другие известные ранее методы.

Мне, конечно, не хотелось бы создать впечатление, что только я обратил внимание на непригодность старых методов конструкции фильтров для создания радиолокационных и телевизионных фильтров или что только я понимал, в чем кроется причина этой непригодности. Просто мой метод впервые позволил указать простой, удобный и разумный способ подхода к общей задаче нахождения наилучших фильтров.

Для того чтобы исследовать потенциальные возможности систем прогнозирования, мы с Байглоу организовали маленькую лабораторию. Кроме нас в ней работали еще два человека. Один из них, отличный механик и электрик, переводил наши идеи в реальные схемы, едва только мы успевали их продумать. Второй был вычислителем, который до этого работал бухгалтером.

Читатель, если ты когда-нибудь захочешь организовать вычислительную лабораторию, последуй моему совету и не бери в качестве вычислителя бывшего бухгалтера, как бы честен и квалифицирован он ни был. Вычислитель должен делать расчеты с определенной степенью точности. Это значит, что он должен учитывать определенное число значащих цифр независимо от того, появляется ли первая значащая цифра в шестом знаке после или в шестом знаке до запятой. Бухгалтер же делает расчеты с точностью до центов, и он будет работать так до судного дня. Какие бы числа ни попадались нашему бухгалтеру в процессе расчетов, он неизменно ограничивался двумя знаками после запятой все равно, были ли это числа порядка миллионов, где даже первый знак перед запятой не имел никакого значения, или порядка нескольких стотысячных.

Быть точным до последнего цента - это было делом его совести, и он просто не мог понять, что физические величины измеряются не в центах, а по скользящей шкале, в которой то, что является центом в одной задаче, может оказаться долларом в другой. В частности, когда ему нужно было вычислить малую разность между двумя большими числами, он никак не мог уразуметь, что эти большие числа должны быть измерены с гораздо большей точностью, чем та точность, с которой мы можем определить их разность.

Я чувствовал огромную ответственность за эту работу. Я старался сделать ее как можно быстрее, хотя как раз к этому я максимально не приспособлен. Не одну ночь я просидел за расчетами, безуспешно стараясь успеть к какому-то крайнему сроку, которого мне никто не назначал. В то время я еще не представлял себе всей опасности бензедрина^* и боюсь, что это серьезно отразилось на состоянии моего здоровья.

^* (Лекарство, употребляемое, в частности, как возбуждающее средство.)

Как бы там ни было, я с огорчением заметил, что груз секретности тяжело давит мне на плечи и что бензедрин играет злые шутки со способностью людей хранить тайны. Я и так не очень скрытен по натуре, а употребление этого лекарства сделало меня просто болтливым, что было совсем не ко времени. Мне пришлось отказаться от бензедрина и поискать более разумное средство для поддержания сил, необходимых, чтобы нести бремя военных тягот.

За нашей работой наблюдал доктор Уорен Уивер из Рокфеллеровского института. Мы с Байглоу несколько раз приезжали к нему для консультаций и для того, чтобы сопоставить свои идеи с представлениями других ученых, работавших над теорией прогнозирования и по проблеме сглаживания радиолокационных данных о движении самолетов. Мы совершили две или три поездки на юг, в Форт Монроу в штате Виргиния и на военную базу на побережьи Северной Каролины. Там мы встретились с сотрудниками Телефонной лаборатории Белла, которые охотно поделились с нами своими соображениями. В результате нам удалось объединить в единое целое весь материал, накопленный всеми работавшими в этой области. Должен сознаться, что несколько раз на этих встречах я засыпал, утомленный дорогой и предшествовавшей тяжелой работой.

Вернувшись домой, мы построили экспериментальную установку, позволяющую генерировать нерегулярные функции того типа, который встречается в задаче о прогнозировании движения самолетов, и затем на основе статистических данных, полученных на этой установке, построили систему прогнозирования. Нам удалось создать систему, которая определяла изменение напряжения во времени, скажем, за полсекунды до того, как это изменение реально наступало. Это позволило проверить правильность нашей теории и выяснить критерии, которыми следует руководствоваться при построении приборов, обеспечивающих хорошее прогнозирование.

Весьма любопытной оказалась и сама задача генерирования нерегулярных кривых со статистически заданной степенью нерегулярности. Мы проектировали на потолок луч света, совершавший более или менее периодическое движение. Затем стремились следовать за этим лучом при помощи другого луча, отражавшегося от зеркала, угол поворота которого определялся поворотом рукоятки определенного прибора. Однако в этом приборе перемещение пятна на потолке не было пропорциональным повороту рукоятки, управлявшей движением зеркала, а довольно сложным образом зависело от характеристик всего прошлого пути зайчика (от интеграла и производных этого пути). Более того, сама рукоятка была соединена с, целой системой пружин и противовесов, и потому у оператора создавалось ощущение, очень далекое от обычного для подобных рукояток. Таким образом, управление движением светового пятна было, во-первых, достаточно сложным, а во-вторых, совершенно необычным. Естественно, что каждый человек реагировал на работу прибора несколько по-своему; поэтому при конструировании системы прогнозирования мы исходили не только из общих характеристик прибора, но и из конкретных возможностей каждого человека, находившегося на определенном уровне тренированности.

За эту работу мы были вознаграждены ясными и последовательными результатами. С одной стороны, мы построили механическую систему, позволившую в значительной степени осветить характер поведения человека, решающего некоторую искусственную задачу, и природу нерегулярного поведения, вызванного участием человека в системе управления. С другой стороны, мы нашли способ воспроизведения основных черт нерегулярного движения самолета в полете. Поэтому мы могли надеяться, что наша теория позволит создавать системы, которые и на практике помогут сбивать реальные самолеты.

Для задачи управления противовоздушным огнем наши идеи имели двоякую ценность. В таких задачах мы сталкиваемся с необходимостью учитывать два субъективных психологических фактора. С одной стороны, характер полета самолета, управляемого пилотом, стремящимся обеспечить безопасность своей машины, в значительной мере зависит не только от технических возможностей самолета, но и от состояния нервной системы человека, так что действия пилота мало отличаются от той гипотетической модели поведения, которую мы построили. С другой стороны, наводчик зенитного орудия по техническим причинам не может идеальным образом следить за целью и, кроме того, совершает случайные ошибки, связанные с ограниченными возможностями его органов чувств и мускулов. Два вида этих субъективных факторов входят в качестве составных частей в тот полумеханизированный процесс, в результате которого зенитное орудие сбивает самолет.

В начале войны единственный известный метод слежения за самолетом заключался в том, что наводчик зенитного орудия должен был держать самолет на прицеле своего орудия, управляя движением орудия вручную. В ходе войны в связи с усовершенствованием радиолокаторов этот процесс был механизирован. Появилась возможность непосредственно связать орудие с радиолокатором, определявшим местоположение самолета, исключив, таким образом, субъективный элемент в операции наведения орудия.

Однако у нас не было ни малейшей возможности устранить психологические факторы в поведении противника, а чтобы иметь возможность дать наиболее полное математическое описание общей задачи управления зенитным огнем, необходимо рассматривать все факторы этой задачи с единой точки зрения - либо с точки зрения человека, либо с точки зрения машины. Поскольку наше понимание процессов в механическом устройстве для наведения орудия на цель было куда более полным, чем понимание психологии пилота, мы решили попытаться построить механические модели поведения наводчика зенитного орудия и пилота самолета.

И в том и в другом случае поведение людей основывается на том, что они наблюдают совершаемые ими ошибки и стараются исправить их, сознательно действуя в направлении, обеспечивающем уменьшение этих ошибок. Такой метод управления показался нам довольно похожим па метод, уже давно известный в электротехнике и начавший в это время применяться в следящих системах и в системах, использующих для целей управления внешние источники энергии, скажем, при управлении грузовиком. Такой принцип управления называется принципом отрицательной обратной связи.

Отрицательная обратная связь может использоваться, например, для управления вращением орудийной башни корабля. Если орудия башни направлены не в том на-правлении, которое определено вычислительным устройством, разница в направлениях используется в качестве сигнала управления устройством поворота башни таким образом, чтобы вызвать поворот этой башни в направлении, заданном вычислительным устройством.

Все физиологи прекрасно знают, что патологическое состояние какого-нибудь органа в значительной мере позволяет уяснить законы его нормального функционирования. Поэтому мы задали себе вопрос, обладают ли системы с отрицательной обратной связью какой-либо ярко выраженной специфической патологией. Такая постановка вопроса является, по-видимому, совершенно закономерной.

Для того чтобы разобраться в общих принципах использования отрицательной обратной связи, рассмотрим пример орудийной башни, поворот которой регулируется простым поворотом рукоятки. Если поворот башни выполняется непосредственно с помощью рукоятки, то одно и то же усилие, приложенное к рукоятке, вызовет различные результаты в зависимости от того, нагрелась ли башня или нет (ибо от этого зависит, является ли смазка жидкой или застывшей). Кроме того, результаты поворота рукоятки будут зависеть и от того, опущены ли орудия башни, так что ее момент инерции относительно вертикальной оси велик, или же эти орудия подняты, что сразу приводит к уменьшению момента инерции. Основная цель использования отрицательной обратной связи в системе управления орудийной башней заключается в том, чтобы сделать реакцию башни более точно пропорциональной усилию, приложенному к рычагу, и, следовательно, меньше зависящей от трения, момента инерции и других внешних условий.

В системе с отрицательной обратной связью зависимость реакции от изменения нагрузки не просто меньше, чем в системах без обратной связи. Эта зависимость становится все меньшей и меньшей по мере того, как все большая и большая часть реакции системы подается обратно на ее вход, - другими словами, по мере того, как повышается коэффициент усиления в цепи обратной связи. Однако такое улучшение характеристик системы не продолжается до бесконечности, так как на определенном этапе при некотором большом значении коэффициента усиления в цепи обратной связи в системе самопроизвольно возникают колебания, система начинает вести себя совершенно диким образом, и зависимость реакции от нагрузки оказывается даже большей, а не меньшей, чем для систем без обратной связи. Мы решили, что если процессы управления в человеческом организме и в самом деле в значительной степени определяются использованием отрицательной обратной связи, то должны существовать условия очень сильной обратной связи, при которых человеческий организм вместо того, чтобы эффективно осуществлять управление, попадет в режим все более и более сильных свободных колебаний, которые будут продолжаться либо до полного разрушения организма, либо до полной перестройки его поведения.

Это соображение, в равной степени принадлежащее мне и Байглоу, я изложил моему другу нейрофизиологу доктору Розенблюту. В то время он еще не переехал в Мексику и работал вместе с доктором Кэнноном в Гарвардской медицинской школе. Мы задали ему конкретный вопрос: не существует ли такого нервного расстройства, при котором у больного в состоянии покоя не наблюдается никакого тремора, но как только он пытается взять, например, стакан воды, у него начинается дрожь, которая становится все сильнее и сильнее до тех пор, пока эта попытка не потерпит полную неудачу, т. е. пока он не прольет воду?

Доктор Розенблют ответил, что такое патологическое состояние хорошо известно и называется интенционным тремором; обычно причина этого заболевания связана с расстройством мозжечка, управляющего целенаправленной мышечной деятельностью человека и определяющего уровень, на котором эта деятельность происходит. Таким образом, оказалось, что наше предположение о значительной роли обратной связи в системе управления человека можно подтвердить ссылкой на бесспорное сходство расстройства систем с обратной связью и общеизвестной в медицине формой патологии целенаправленного организованного поведения человека.

Около двух лет тому назад мне самому пришлось столкнуться с событием, которое можно рассматривать как иллюстрацию к излагаемым здесь идеям. Совершенно неожиданно моя маленькая внучка, жившая тогда у нас, заболела интенционным тремором того типа, о котором я только что рассказал. Мы сразу же отвезли ее в больницу и узнали, что заболевание вызвано особой формой энцефалита, затронувшего мозжечок. Положение было очень серьезным, но по счастливой случайности девочка полностью выздоровела, избежав каких бы то ни было остаточных явлений. Если бы я был суеверен, ее заболевание и многие другие похожие случаи, о которых рассказывали мне врачи, заставило бы меня поверить, что болезнь - это злобное существо, с особенным удовольствием мстящее ученым, которые с ней борются.

Теперь я хочу вернуться к работе нашей тройки. Мы изложили свои идеи в статье, но, главное, мы с Байглоу почувствовали, что можем уверенно обращаться с субъективными факторами в системе управления, рассматривая их просто как дополнительные технические элементы с обратной связью. В результате этого мы пришли к выводу, что можем уже перейти от наших грубых экспериментальных установок к созданию полной системы управления противовоздушным огнем.

Было очевидно, что в принципе система управления огнем зенитной артиллерии должна быть системой с обратной связью, содержащей множество второстепенных обратных связей, характеристики которых должны были влиять на всю систему в целом. На самом деле эти характеристики были нам неизвестны, поэтому можно было рассчитывать лишь на создание весьма несовершенной и плохо отрегулированной установки.

Исходя отсюда, было решено, что нет особого смысла развивать дальше работу в этом направлении отчасти еще потому, что предварительные математические расчеты не давали надежды на особенно высокое качество работы подобных систем управления.

Наши идеи были с энтузиазмом подхвачены другими специалистами в этой области и в конечном счете привели к определенному повышению качества практически используемых систем, в частности систем для отделения ошибок экспериментальных данных. Окончательно отработать конструкцию предложенной системы слежения нам не поручили; вместо этого меня попросили написать книгу, посвященную временным рядам, экстраполяции и интерполяции. Эта книга была размножена фотолитографским способом и благодаря желтой суперобложке получила название "Желтой опасности", перехватив это прозвище у книг математической серии, выпускаемой немецким издательством Шпрингера в одинаковых желтых переплетах. Мой учебник довольно широко использовался проектировщиками систем управления наводкой и огнем зенитной артиллерии во время войны, а также специалистами по следящим системам и системам связи, которым он оказался полезен и в военные и в послевоенные годы. После войны книга была еще раз переиздана в расширенном и переработанном виде с приложением, написанным профессором Норманом Левинсоном, помогающим лучше уяснить способы применения предложенного метода.

Проделанная мною работа по статистической теории управления огнем зенитной артиллерии привела в конце концов к выработке общей статистической точки зрения на проблемы связи. За прошедшие годы эта точка зрения стала общепринятой, но это еще не самое главное. Более важно то, что в настоящее время статистический подход проникает почти во все разделы техники и что этот подход находит сейчас применение и в таких бывших ранее далекими от математики областях, как метеорология, социология и экономика.

Теперь я хотел бы вернуться к своим предыдущим замечаниям, касающимся Уилларда Гиббса и того переворота, который он и его современники совершили в физике. Ортодоксальная ньютоновская точка зрения на физическую динамику сводит законы природы к определенным уравнениям, называемым дифференциальными уравнениями относительно скоростей изменения неизвестных параметров. С помощью этих уравнений скорость изменения физических параметров может быть определена по их значениям, и зная начальные значения (т. е. значения в нулевой момент времени) наших параметров, мы можем шаг за шагом проследить во времени все течение описываемого явления. В самом деле, в каждый момент времени мы будем знать значения всех интересующих нас параметров; но тогда по этим значениям мы определим также и скорость их изменения, а это уже позволяет нам приближенно определить значения наших параметров и в близкий последующий момент времени.

Выбрав какой-то достаточно короткий промежуток времени, мы можем, двигаясь такими небольшими шагами, в конце концов определить значения всех интересующих нас параметров в любой наперед заданный момент. Именно так поступают астрономы, рассчитывая орбиты планет, и специалисты по баллистике, определяя траектории вылетающих из орудия снарядов.

В астрономии, как я уже говорил раньше, расчет орбит производится с очень большой точностью и с такой же точностью определяются и все исходные данные. Однако в баллистике, как и в большинстве других технических дисциплин, дело обстоит совсем не так. В момент выстрела, например, мы можем определить угол прицеливания лишь с весьма ограниченной точностью. То же самое справедливо и относительно веса снаряда, мощности заряда и параметров, характеризующих атмосферные условия. В результате с самого начала вместо точных значений всех параметров задачи мы располагаем лишь определенными диапазонами их возможных значений. Классический метод решения такой баллистической задачи состоит в том, что исходные данные сперва считаются точно известными. После этого определяют дальность действия, угол встречи, скорость при ударе и другие существенные параметры. Затем полученные результаты пересматриваются с помощью методов интерполяции или коррекции, в корне отличных от тех методов, которые использовались на первом этапе решения. При этом мы довольно бессмысленно расходуем значительные усилия сначала на то, чтобы обеспечить нереальную точность наших результатов, а затем на то, чтобы скорректировать эти недостаточно реальные данные. Существует, однако, другой метод, который все более и более начинает распространяться в последнее время; духовным отцом этого метода и является Уиллард Гиббс.

Гиббс отметил, что с процессом изменения состояния динамической системы, происходящим в соответствии с законами физики, например со свободным вращением волчка, можно связать другой процесс, очень напоминающий течение жидкости. Для того чтобы описать движение волчка, нужно указать определенную точку в некотором пространстве, существенно отличающемся от обычного трехмерного пространства, знакомого всем из курса стереометрии. Для определения положения волчка необходимо задать шесть "координат", и еще шесть "координат" требуется для описания скоростей их изменения (или тесно связанных со скоростями импульсов). Все эти величины образуют набор из двенадцати чисел, и совокупность всех таких наборов можно по аналогии назвать двенадцатимерным пространством. Оказывается, что в этом пространстве существует мера объема такая, что множество волчков, заполняющих в какой-то момент определенный объем, заполняло бы точно тот же объем и в любой другой момент времени. Такой не меняющийся во времени объем можно ввести для всех динамических систем, движение которых не сопровождается притоком или расходом энергии.

Поток, напоминающий поток жидкости, о котором мы упоминали выше, можно рассматривать как поток вероятности; именно так его и интерпретировал Гиббс. Вероятность того, что частица в определенный момент времени попадет в определенную область этого странного пространства, оказывается равной вероятности того, что она через некоторое время попадет в другую область, а именно в ту, в которую в процессе своего движения перейдет исходная область.

Типичные уравнения, описывающие такой поток, уже не принадлежат к классу так называемых обыкновенных дифференциальных уравнений, а являются интегральными. Эти интегральные уравнения связывают распределения вероятностей в прошлом с распределениями вероятностей в будущем. Получаемая связь оказывается при этом такой, что если в начальный момент времени мы будем иметь сумму нескольких разных распределений, то и в будущие моменты времени получим распределение вероятностей, являющееся суммой распределений, получаемых из каждого из тех, которые имелись вначале. Подобная система, реакция которой на сумму входных воздействий оказывается равной сумме реакций на отдельные воздействия, называется линейной. Соответственно этому и интегральные уравнения потока, описывающего динамику всевозможных аналогичных систем, также надо считать линейными.

Описанный метод весьма удобен для практических расчетов; в случае же очень сложных задач он часто оказывается гораздо более простым, чем классический метод Ньютона. В несколько упрощенном виде этот метод сейчас широко практикуется некоторыми сотрудниками технического отделения МТИ.

Кроме достоинств, связанных с простотой расчета более сложных задач, этот метод по сравнению с ньютоновским имеет принципиальное преимущество с логической точки зрения. Ведь на самом деле уменьшение точности конечных результатов объясняется вовсе не одной только неточностью уравнений и неточностью определения начальных условий; вообще все имеющиеся у нас данные содержат принципиальную неточность. Поэтому бессмысленно сначала получать результат с искусственно повышенной точностью, а затем специально изучать ошибки при расчете, с тем чтобы выяснить его реальную точность. Мы можем с самого начала выложить все наши карты на стол; в конце концов при этом мы получим ровно то, что нам нужно, не больше и не меньше. Такой подход не только позволяет сэкономить много ненужных усилий, но и приводит к повышению реальной точности расчетов.

Никакие физические измерения не являются абсолютно точными, и уже поэтому все теоретические расчеты, основывающиеся на неточных данных, также приводят к неточным результатам. Классическая ньютоновская физика приписывает неточным данным точность, которой они не обладают, определяет по этим данным решение задачи, а затем понижает точность этого решения с помощью учета неточности исходных данных. В современной физике, в отличие от ньютоновского подхода, при использовании неточных данных ученые стремятся с самого начала учитывать истинную точность наблюдений, не стараясь ни на одном этапе вычислений получить большую точность, чем та, которая на самом деле является реальной.

Если бы при решении таких задач с неточными данными мы воспользовались методом, которым пользуется астроном, определяя орбиты планет, то вполне могло бы оказаться, что мы выбрали такие начальные условия, которые приводят к результатам, не типичным для более широкого круга начальных условий, с которыми мы на самом деле сталкиваемся в исследуемой задаче. Такая нестабильность траектории может привести к неверному представлению о возможной ошибке в конечных результатах.

Как я уже говорил раньше, рассказывая о моей работе по теории прогнозирования, наиболее чувствительные из наших приборов оказываются и самыми неустойчивыми. Неустойчивость же приводит к ошибкам, вообще говоря, отличающимся от ошибок, связанных с неточностью прибора, но не менее серьезным. То, что я говорил о физических приборах, справедливо и относительно вычислительных методов. Компромисс между ошибками, связанными с неточностью данных, и ошибками, связанными с не-устойчивостью методов, может быть найден только на основе статистических рассмотрений. Почему же тогда нельзя встать на статистическую точку зрения с самого начала и вычислять одновременно как средний результат, так и ошибку этого результата с единой точки зрения? И если такое признание статистической природы науки уже сейчас принесло большую пользу во многих технических задачах ньютоновского типа, то во сколько же раз эта польза будет больше при таком подходе к решению задач, в которых ошибки наблюдения обычно очень велики!

В качестве примера возьмем метеорологию. Мы достаточно хорошо знакомы с законами динамики атмосферы, и если бы можно было с высокой точностью определять начальные условия для метеорологических задач, то можно было бы решать эти задачи чисто ньютоновским методом, хотя и в этом случае пришлось бы затратить много лишних усилий.

Однако на самом деле для определения состояния атмосферы берется по три, четыре пробы в день на сотню тысяч кубических миль атмосферы.

Недавно по предложению Джона фон Неймана была предпринята попытка решения задачи прогноза погоды, при которой эта задача рассматривалась как некоторая очень сложная задача того же типа, что и астрономическая задача об определении планетных орбит. Идея заключалась в том, чтобы ввести все данные о начальном состоянии атмосферы в сверхмощную вычислительную машину и, используя затем законы движения, выражаемые уравнениями гидродинамики, рассчитать погоду на продолжительное время вперед.

Однако основное препятствие на этом пути состоит в том, что бюро прогнозов располагает лишь ограниченной информацией о состоянии атмосферы в отдельных точках, разделенных колоссальными промежутками. Это препятствие можно как-то преодолеть, лишь прибегнув к помощи статистических методов. Поэтому наиболее соответствующим природе задачи здесь был бы метод, органически объединяющий динамические и статистические соображения. Существуют определенные доводы, показывающие, что статистические соображения в метеорологии можно отбросить, лишь вообще отказавшись от любых исследований.

Разумеется, я не собираюсь отрицать значение классической механики; мне хотелось бы, однако, обратить внимание на важные преимущества подхода Гиббса, при котором законы динамики используются для построения некоторого статистического потока.

Положение дел в метеорологии является типичным для всех тех наук, которые лишь недавно стали рассматриваться как точные и использовать количественные методы. В экономике так называемая эконометрика, изучающая экономическую динамику, жестоко страдает от того, что исходные числовые данные в ее задачах никак не могут быть точно определены и должны заменяться грубыми оценками. Кто может сказать, как точно определить, что такое спрос, и как измерить его таким образом, чтобы это удовлетворило сразу всех экономистов? И разве могут совпасть мнения двух экономистов о размерах безработицы в США в данный момент времени?

Эконометрика не сдвинется с мертвой точки, пока не будут сделаны два следующих шага. Во-первых, необходимо, чтобы все величины, рассматриваемые в эконометрике, такие, как спрос, объем запасов и тому подобное, определялись с той же степенью точности и строгости, с которой рассчитываются соответствующие динамические процессы. Во-вторых, с самого начала нужно признать статистический и недостаточно точный характер этих величин и вытекающую отсюда необходимость гиббсовского подхода к их исследованию.

Все сказанное о метеорологии и экономике в равной степени справедливо и для изучения динамических процессов в социологии, для биометрики и в особенности для крайне сложной проблемы изучения нервной системы, так сказать, метеорологии мозга. Это азбучные истины принципов использования математического метода в науках, находящихся на полпути между точными и гуманитарными. Я думаю также, что эти соображения будут играть центральную роль и в технике будущего.

Новые методы, о которых я говорю, в какой-то степени содержались уже в моих работах военных лет по системе упреждения для управления огнем зенитной артиллерии и в моих последующих работах по теории связи. Пока эти методы освоены лишь небольшим числом специалистов, работающих в некоторых специальных областях науки и техники, но они опираются на здоровью философские принципы и обещают решительно изменить лицо всех точных или хотя бы полуточных наук.

Когда я писал свою первую работу по теории прогнозирования, я не предполагал, что некоторые из основных математических идей этой статьи были уже опубликованы до меня. Но вскоре я обнаружил, что незадолго до второй мировой войны советский математик Колмогоров напечатал в "Докладах" Французской академии наук небольшую, но очень важную заметку, посвященную этой же теме. В своей работе Колмогоров ограничился изучением прогнозирования для дискретных последовательностей, в то время как я изучал случаи непрерывного времени. Колмогоров ничего не говорил о фильтрах и вообще не касался вопросов, имеющих хоть какое-нибудь отношение к электротехнике. Кроме того, он не указывал никаких путей физической реализации своих систем прогнозирования или возможности их использования для управления огнем зенитной артиллерии.

Тем не менее все идеи по этому поводу, которые мне казались действительно глубокими, появились в заметке Колмогорова до того, как я опубликовал свою статью, хотя я и узнал об этом только через некоторое время. Работы Колмогорова и таких его учеников; как Крейн^*, продолжали появляться в "Докладах" Академии наук СССР, и хотя эти статьи в основном базировались на представлениях о теории прогнозирования, которые были развиты Колмогоровым в его первой статье и были несколько уже моих концепций, у меня нет никакой уверенности в том, что Колмогоров самостоятельно не нашел также и известных мне возможностей применения этих методов.

^* (На самом деле одесский математик проф. М. Г. Крейн не является учеником Колмогорова, но его работа по теории прогнозирования действительно возникла в результате разговоров с Колмогоровым. (Прим. ред.))

Если дело обстояло именно так, ему, наверное, просто не удалось опубликовать свои результаты в открытой печати ввиду того, что они имели военное значение. Недавняя статья Крейна, в которой он прямо ссылается на мои прикладные работы, еще более убеждает меня в этом.

Я никогда не встречался с Колмогоровым, никогда не был в России и никогда не переписывался ни с ним, ни с кем-нибудь из его учеников^*.

^* (После написания этой книги Винер в 1960 г. посетил СССР. 250)

Все, что я говорю о нем, в значительной степени основано на догадках. Когда я только еще начинал работать для Военного министерства США и ничего не знал о статье Колмогорова, возник вопрос, не интересуется ли кто-нибудь за границей теми же проблемами, что и я. Я говорил тогда, что немецкие ученые вряд ли подготовлены к работе в этой области, что мои друзья Крамер в Швеции и Леви во Франции вполне могли бы увлечься теми же идеями, но что если кто-нибудь в мире занимается сейчас тем же, что и я, то, вероятнее всего, это Колмогоров в России. Я сказал это, исходя из того, что за последние двадцать-тридцать лет почти ни разу ни один из нас не опубликовал какой-нибудь работы без того, чтобы очень скоро не появилась тесно связанная с ней работа другого на ту же тему.

Года два-три тому назад мне попалась русская книга по теории связи, прогнозирования и другим тесно связанным вопросам, в которой приводилось множество ссылок на мои работы и работы Колмогорова. В этой книге приоритет признавался за Колмогоровым, и хотя это справедливо лишь отчасти, все же, как я уже говорил, вполне можно утверждать, что Колмогоров не только независимо разобрал все основные вопросы в этой области, но и был первым, опубликовавшим свои результаты. Мои собственные работы рассматриваются в русской книге очень обстоятельно, и их оценка является гораздо более объективной, чем та, на которую можно было бы рассчитывать при нынешних отношениях между нашими странами.

"Желтая опасность" по-прежнему играет важную роль в современной исследовательской жизни Америки как в военных, так и в открытых исследованиях. С разрешения правительства она была переиздана; экземпляр этой книги, должно быть, попал в Россию, что и послужило основанием для тех замечаний, о которых я только что говорил.

С определенной точки зрения мою работу, или, точнее, работу нашей группы, можно считать покрывающей очень широкую область теории и практики связи. Прежде всего "Желтая опасность", без сомнения, представляет собой статистическое исследование вопросов теории связи. В то время, когда книга писалась, почти никто не рассматривал теорию связи с этой точки зрения. Поэтому я думаю, что мне можно извинить некоторую гордость, которую я испытываю сегодня в связи с тем, что статистический подход к вопросам теории связи получил повсеместное распространение.

Я подошел к теории информации с позиций изучения электрических систем, проводящих непрерывный ток или что-нибудь такое, что по крайней мере может быть интерпретировано как непрерывный ток. В то же время Клод Шеннон из Телефонной лаборатории Белла параллельно разрабатывал близкую и во многом эквивалентную теорию с точки зрения теории электрических переключательных схем. Эта работа представляла собой непосредственное развитие его предыдущих работ, посвященных использованию алгебры логики для решения задач теории релейных схем.

Как я уже говорил выше, Шеннон любит дискретное и сторонится непрерывного. Он рассматривает дискретные сообщения как последовательность во времени утвердительных и отрицательных ответов, и каждый выбор между "да" или "нет" считает элементом информации. В то же время я, занимаясь теорией непрерывной фильтрации и исходя из точек зрения, казавшихся вначале совершенно отличными от точки зрения Шеннона, пришел к весьма близкому определению единицы количества информации.

Введя определение понятия количества информации по Шеннону - Винеру (ибо оно в равной мере принадлежит нам обоим), мы совершили радикальный переворот в этой области. В течение многих лет предполагалось, что пропускная способность линии связи за единицу времени определяется шириной полосы частот, используемой этой линией. Считалось, что по линии с шириной полосы частот? в 200 гц можно передать за одно и то же время в два раза больше информации, чем по линии с полосой пропускания в 100 гц. При этом игнорировался тот факт, что при передаче в отсутствие шумов любая полоса частот окажется достаточной для того, чтобы можно было передать любую информацию за одну секунду. Одно значение мгновенного напряжения, измеренное с точностью до одной десяти триллионной, могло бы передать всю информацию, содержащуюся в Британской энциклопедии, если бы только шумы в наших цепях не ограничивали возможную точность измерения пределами порядка одной тысячной.

Первое время после изобретения телефона лишь очень немногие линии были загружены до предела пропускной способности. Однако с развитием телефонии и появлением новых способов связи, таких, как радио и телевидение, возникла необходимость в более полном использовании имеющихся возможностей передачи сообщений. Стало ясно, что уровень шумов в линиях или воздушном канале связи является еще одним важным фактором, требующим пристального внимания. Весь эфир заполнен возмущениями, которые радисты называют атмосферными помехами, и ни один проводник, будь он металлическим или газовым, не может переносить электричество порциями, меньшими чем заряд одного электрона. Пульсации, связанные с нерегулярностью потока электронов, получили название дробового эффекта, и их учет играет важную роль при проектировании современных систем связи.

Лишь совсем незадолго до второй мировой войны нагрузка линий связи возросла настолько, что неизбежные шумы стали серьезным препятствием на пути еще большего повышения их загруженности. При этом статистический подход к теории связи, который я в какой-то мере предугадал в своих старых работах по обобщенному гармоническому анализу и которому мы вместе с Шенноном придали столь большое значение в наших работах периода начала войны, вскоре после войны стал основным методом исследования в подавляющем большинстве работ.

Наша работа, посвященная теории обратной связи в приложении к системам управления зенитным огнем и нервной системе человека, привела к еще одному перевороту, который, как и первый, получил повсеместное признание за последние несколько лет. Когда я впервые начал работать в МТИ, электротехника делилась на два основных раздела, которые в Германии назывались электротехникой слабых и электротехникой сильных токов, а в Соединенных Штатах - электроэнергетикой и электросвязью.

Между этими двумя областями действительно существует принципиальное различие, но его сущность и точное положение границы раздела в течение длительного времени оставались неясными. Генераторы телевизионной станции или радиостанции, ведущей трансатлантические передачи, могут вырабатывать относительно большие мощности; в то же время слабенький двигатель в бормашине у зубного врача потребляет лишь малые доли лошадиной силы. Тем не менее в первом случае электричество явно используется прежде всего для обеспечения связи, а во втором служит лишь источником энергии.

В эпоху, когда истинная природа различия между двумя разделами электротехники еще не была полностью понятна, естественно, считалось, что следящие системы, управляющие движением орудийной башни, как и все другие части мощных и громоздких устройств, должны относиться к области электроэнергетики, а не электросвязи. Существенно отметить при этом, что в электроэнергетике сложилась определенная традиция рассматривать все электрические токи и напряжения как величины, непрерывно меняющиеся во времени, в то время как в теории связи, в первую очередь под влиянием работ Хевисайда, принято было рассматривать сигналы как суммы большого или даже бесконечного числа гармонических колебаний различных частот. В то время было совсем не легко понять, что в теории следящих систем и автоматического регулирования, так же как, например, в телефонии или телевидении, наиболее удобным является именно частотный подход к задачам, а не подход, исходящий из представления всех процессов в виде явных функций времени.

Мне кажется, что я могу гордиться тем, что впервые отчетливо это понял и отнес теорию следящих систем к области теории связи. Исходя из своих общих идей, я рассматривал автоматические вычислительные машины также как одну из форм систем связи, поскольку основное внимание здесь уделяется передаче сигналов, а не мощностей. С моей точки зрения, такие системы представляют собой просто последовательность переключающих устройств, соединенных между собой таким образом, что информация, содержащаяся в сигнале на выходе каких-то из них, используется в последующих устройствах в качестве входного сигнала и сигнала управления.

Ясно, что такие переключающие устройства могли реализоваться и в форме зубчатых колес или других подобных механизмов, и в форме механических или электрических реле, использующих электронные лампы или другие средства электроники. Как я уже говорил, мне казалось, что наиболее удобными будут переключающие устройства, которые осуществляют выбор между двумя, а не десятью возможностями, и я попытался популяризировать эти идеи среди широких кругов инженеров.

Вскоре я познакомился с первой из новых цифровых машин, построенных на реле. Она находилась в Гарвардском университете. Работы по созданию этой машины велись по правительственному заданию, и руководил ими Говард Эйкен. Его успехи произвели на меня большое впечатление и вызвали чувство глубокого восхищения. Эйкен рассматривал свою машину как современный вариант тех весьма примитивных вычислительных машин, которые около ста лет тому назад разрабатывал Бэббедж в Англии. В свое время Бэббедж прекрасно разобрался в математических возможностях вычислительных машин, но совершенно не понял возникающих при этом чисто технических задач.

Меня очень удивило, что Эйкен в качестве основных элементов своей машины выбрал сравнительно медленно действующие механические реле, не придав особого значения громадному увеличению скорости вычислений, которого можно было бы достигнуть, используя электронные реле. Порочность этой точки зрения в настоящее время очевидна, в частности благодаря самому Эйкену, ставшему одним из наиболее энергичных и оригинальных изобретателей и конструкторов электронных вычислительных машин. Но тогда у него была какая-то странная причуда, заставлявшая его считать работу с механическим реле нравственной и разумной, а использование электронных реле - делом, никому не нужным и морально нечистоплотным.

В этой связи мне хочется напомнить об одном чрезвычайно опасном свойстве, которым часто отличаются наиболее талантливые и целеустремленные изобретатели. Люди такого склада обычно стремятся навеки законсервировать технические приемы своей области на том уровне, которого они сами достигли, и проявляют чудеса моральной и интеллектуальной изворотливости, сопротивляясь, а иной раз даже воздвигая непреодолимые препятствия на пути новых работ, основанных на новых оригинальных принципах. Мы, математики, нуждаемся лишь в таких недорогих материалах, как бумага и, быть может, типографская краска, и мы давно примирились с мыслью, что при работе в какой-нибудь бурно развивающейся области наши открытия начинают устаревать в тот самый момент, когда они изложены на бумаге, и даже раньше - в момент, когда они еще только зарождаются в наших умах. Мы знаем, что в течение долгого времени все наши результаты будут служить лишь отправными точками для других ученых, работающих над теми же проблемами и заранее предвидевших все то, что нам удалось достигнуть. Именно в этом и заключается смысл знаменитого изречения Ньютона, сказавшего: "Если я видел дальше, чем другие, то потому, что я стоял на плечах гигантов".

В то же время коммерческие возможности, связанные с изобретательством, заставляют людей, работающих в промышленности, закрывать глаза на этот основной факт и надеяться, что им удастся остановить прогресс как раз на том уровне, которого они смогли достичь. Изобретателей толкает на этот путь патентная система и коммерческое отношение к техническим идеям как к объекту продажи. Однако такой взгляд на вещи безусловно не реалистичен. Изобретатель, как практик, должен иметь практическое чутье, подсказывающее ему, что в течение многих лет его основным достижением будет не изобретение какого-нибудь одного устройства, а содействие рождению нового круга идей, касающихся широкого класса технических устройств прошлого, настоящего и будущего. Он должен работать в согласии с этим новым кругом идей и должен понимать, что раз ему удалось превзойти тех, кто жил до него, то и его работа неизбежно послужит лишь фундаментом для будущих работ, а не останется навеки последним словом науки и техники.

Что касается меня, то личная заинтересованность в развитии вычислительных машин увела меня далеко за пределы круга идей, связанных с прошлым, настоящим и будущим машин, сделанных из латуни, меди, стекла и стали. Человеческий мозг и нервная система в некоторых отношениях также напоминают вычислительные машины. Подобно тому, как на выходе реле возможны лишь два сигнала "да" и "нет", для нервного волокна возможны лишь два основных состояния: состояние, в котором по волокну передается сигнал, и состояние, в котором никакого сигнала не передается. К этому сводится проявление известного принципа "все или ничего" в деятельности нервной системы, и хотя приведенная здесь нарочито грубая и упрощенная формулировка этого принципа, воз-можно, и не является вполне точной, она достаточно хорошо определяет основную закономерность передачи раздражений по нервным тканям.

Нервное волокно, правда, может быть приведено в раздражение при помощи сигналов различной интенсивности, но в конце концов возможны лишь два исхода: либо возникшее раздражение затухнет в волокне, так и не дойдя до его конца, либо же в волокне возникнет то, что химики называют процессом автокатализа, и появится электрический импульс, который от одного конца волокна дойдет до другого. В тот момент, когда этот импульс до-ходит до второго конца нервного волокна, он оказывается уже практически не зависящим от интенсивности исходного раздражения, и следовательно, эту интенсивность можно не принимать во внимание. Таким образом, между нервным волокном и электрическим триггером - цепью с двумя и только двумя состояниями равновесия - существует определенная аналогия. Эта аналогия оказывается очень полной, так как уже задолго до того, как сигнал достигает конца нервного волокна, вся содержащаяся в нем полезная информация заключается лишь в числе импульсов, а не в их величине (т. е. интенсивности).

Нервные волокна являются не только переключающими устройствами, но и входят как составная часть в целую систему переключающих устройств. Они соединяются друг с другом в особых точках или узлах, называемых синапсами. При этом ответ на вопрос о том, будет или не будет распространяться сигнал по выходящему из синапса волокну, зависит от всего множества сигналов, пришедших в этот синапс по входным волокнам. В простейших случаях синапс просто характеризуется определенным порогом раздражимости, т. е. выходное волокно раздражается и передает сигнал, если за какой-то определенный критический промежуток времени входные волокна передают больше какого-то определенного числа сигналов, и не раздражается, оставаясь невозбужденным, если этого не происходит.

В повседневной жизни мы так привыкли к явлению обратной связи, что часто забываем о его роли в самых простых процессах. Если нам удается стоять на ногах, то достигается это совсем иначе, чем в случае, например, статуи, так как для того, чтобы удержать в вертикальном положении самую устойчивую статую, ее нужно все же прикрепить к какому-то пьедесталу. Люди стоят потому, что они непрерывно сопротивляются тенденции упасть вперед или назад и умеют непроизвольно компенсировать эти тенденции с помощью мускульных усилий, отклоняющих тело в обратном направлении. Равновесие человеческого тела, так же как и другие виды равновесия, наблюдаемые в живых организмах, не является статическим, а достигается за счет непрерывно протекающих процессов, активно препятствующих развитию любой тенденции, направленной на то, чтобы его нарушить. Таким образом, стоя на месте или передвигаясь, мы непрерывно сражаемся с силами земного притяжения, а вся наша жизнь есть непрекращающаяся борьба со смертью.

Все эти соображения заставили меня склониться к мысли, что нервная система человека является неким аналогом вычислительной машины, и я поделился своими соображениями с доктором Розенблютом и другими нейрофизиологами. Мне удалось собрать группу нейрофизиологов, инженеров-связистов и специалистов по вычислительной технике на неофициальный семинар в Принстоне. Выяснилось, что представители каждой из этих профессий были очень рады познакомиться с работами своих коллег и воспользоваться новой для себя терминологией. В результате специалисты в этих различных областях очень быстро начали говорить на одном языке, словарь которого содержал термины, заимствованные и у инженеров-связистов, и у специалистов по автоматическому регулированию, и у нейрофизиологов.

Например, всех их интересовали вопросы хранения информации, предназначенной для использования впоследствии, и все пришли к выводу, что слово память (широко применяемое в нейрофизиологии и психологии) хорошо подходит для того, чтобы объединить разнообразные методы хранения информации, рассматриваемые в различных областях науки и техники. Все согласились также, что термин обратная связь, впервые появившийся в электротехнике и подхваченный специалистами по автоматическому регулированию, правильно описывает многие явления не только в машинах, но и в живых организмах. Наконец, все были согласны измерять количество информации числом ответов типа "да" или "нет" и в конце концов остановились на термине "двоичная единица" или "бит"^* для обозначения этой единицы количества информации. Я считаю, что встреча в Принстоне дала жизнь новой науке кибернетике - теории управления и связи в машинах и живых организмах.

^* (Сокращение английского термина "binary digit", т. е. "двоичная цифра".)

Я надеялся, что новая наука будет быстро развиваться в самых различных направлениях. Со временем кибернетика действительно сделала огромные успехи, и в них есть и моя доля труда. Но тогда обстановка не благоприятствовала нормальному распространению новых идей, и мне пришлось долго ждать, пока к тому, что я считал серьезным вкладом в науку, в обществе перестали относиться как к научной фантастике и пустой погоне за сенсацией.

В наше время научная фантастика стала модой; даже серьезные ученые пишут теперь научно-фантастические романы и считают это своей заслугой. Ребенком я сам страстно увлекался Жюлем Верном и Гербертом Уэллсом, отцами современной научно-фантастической литературы, но то, что пишется сейчас, делается гораздо более ловко и приносит несравненно больше вреда. С одной стороны, такого рода литература возбуждает инстинкты насилия и жестокости, оказывая такое же пагубное влияние, как лишенные комизма комиксы или гангстерские истории, в которых "ощупью крадутся в темноте, и мертвые тела падают на землю с глухим стуком". С другой стороны, эта литература способствует воспитанию поколения молодежи, которое, овладев языком научно-фантастических произведений, считает, что оно мыслит научными терминами. Наши учебные заведения, занимающиеся подготовкой научных и технических кадров, испытывают серьезные затруднения, перевоспитывая юношей, которые решили посвятить себя науке только потому, что привыкли играть с идеями всеразрушающих сил, иных миров и ракетных путешествий.

Все эти порочные сказки в значительной степени порождены второй мировой войной, в результате которой целое поколение ученых оказалось почти полностью деморализованным. Во время войны положение науки, и в частности математики, резко изменилось. Прежде всего, из жизни людей совершенно исчез досуг. До войны в какой-нибудь комнате отдыха Уокер Мемориал^* нередко можно было наткнуться на группу студентов МТИ, развлекающихся одной-двумя партиями бриджа.

^* ( Уокер Мемориал (Walker Memorial) "название одного из зданий МТИ.)

Мне частенько случалось играть с ними. Я не считал это время потерянным ни для себя, ни для них, потому что в перерыве между партиями возникали самые разнообразные споры, которые иногда превращались в пустой студенческий треп, а иногда приводили к интересному столкновению идей. С того момента, как началась война, все стали убийственно серьезны, возможности какой бы то ни было интеллектуальной игры оказались крайне ограничены. Даже сейчас, спустя много лет после того, как война кончилась, трудно встретить молодых людей, которые осмелились бы оторвать время от своей работы, чтобы подумать о том, что эта работа собой представляет. По-моему, часы, проведенные за чтением фантастических историй о космическом пространстве, не могут заменить хорошей студенческой трепотни.

Перед войной, особенно в период депрессии, доступ в науку был сильно затруднен. К тем, кто хотел заниматься научной работой, предъявлялись очень высокие требования. Во время войны произошли два существенных изменения. Во-первых, обнаружился недостаток в людях, способных осуществить все необходимые для войны научные проекты. Во-вторых, поскольку их все равно нужно было осуществлять, пришлось перестроить всю систему так, чтобы иметь возможность использовать людей с минимальной подготовкой, минимальными способностями и минимальной добросовестностью.

В результате молодые люди вместо того, чтобы готовиться к долгому и трудному пути, жили с легким сердцем, не беспокоясь о завтрашнем дне, считая, что бум в науке будет продолжаться вечно. Дисциплина и тяжелый труд были для них не обязательны, и надежды, которые они подавали, расценивались ими как уже исполненные обещания. Ученые старшего поколения задыхались от недостатка помощников, от нехватки рабочих рук, а зеленые юнцы выискивали хозяина, который спросит поменьше, но зато не поскупится на лесть и деньги и проявит максимальную терпимость.

Это было одним из проявлений общего падения нравов, начавшегося тогда среди ученых и продолжающегося до сих пор. Почти во все предыдущие эпохи в науку шли только те, кого не пугала суровость труда и скудость результатов. У Теннисона в стихотворении "Северный крестьянин. Новое летоисчисление" есть такая строка: "Не женись из-за денег, но иди туда, где они есть!".

В соответствии с этой мудростью честолюбивые люди, относящиеся к обществу недостаточно лояльно, или, выражаясь более изящно, не склонные терзаться из-за того, что тратятся чужие деньги, когда-то боялись научной карьеры, как чумы. А со времен войны такого рода авантюристы, становившиеся раньше биржевыми маклерами или светочами страхового бизнеса, буквально наводнили науку.

Нам пришлось отказываться от многих старых представлений. Мы все знали, что у ученых есть свои недостатки. Среди нас были педанты, любители спиртного, честолюбцы, но при нормальном положении вещей мы не ожидали встретить в своей среде лжецов и интриганов.

Расставшись со своей уединенной жизнью и погрузившись в научный водоворот военного времени, я начал понимать, что среди тех, кому я доверяю, есть люди, не заслуживающие ни малейшего доверия. Не один раз мне приходилось переживать жестокое разочарование, и каждый раз это причиняло боль.

Вскоре после событий в Пирл-Харборе состоялось заседание, созванное для объединения усилий ученых, работавших в области теории связи. Читатель, наверное, удивлен, что, говоря столько времени о войне, я ничего не сказал о Пирл-Харборе и о формальном вступлении Америки в войну. Я не сделал этого потому, что все мы давно были убеждены в неизбежности войны - как именно это произойдет, в конце концов было не так уж важно, - и начало войны ничего не изменило в моей оборонной работе.

Осенью 1941 года напряжение, созданное разгромом союзников в Норвегии, Голландии и Франции, битвой за Англию и зыбкостью ситуаций в Северной Африке, достигло предела, а тут еще оно осложнилось почти всеобщей уверенностью, что в Японии тоже что-то готовится.

Никто из нас не ожидал того, что произошло в Пирл-Харборе, но, кажется, никто не сомневался, что в условиях военной диктатуры Япония не станет разыгрывать войну согласно общепринятым дипломатическим церемониям, тем более, что это явно было бы нам на руку. Поэтому я, по крайней мере, воспринял Пирл-Харбор как позор и унижение, но не как что-то неожиданное.

События в Пирл-Харборе, непосредственно вызвавшие вступление Америки во вторую мировую войну сразу на обоих полушариях, имели для меня лично ряд серьезных последствий. Мне не пришлось более активно включаться в военные исследования, потому что я уже больше года делал в этом направлении все, что мог. Но война полностью разрушила наши планы - мои и Мануэля Сандо-валя Байарты: мы собирались поехать в Южную Америку с миссией доброй воли; основные средства на поездку должен был дать Государственный департамент (или, если бы с просьбой пришлось обращаться Байарте, мексиканское правительство).

Еще больше мучил меня вопрос, что же теперь будет с моими друзьями Ли. Мы, наконец, получили для них разрешение приехать в Америку на одном из пароходов, отплывавшем из Гонконга. А тут разыгрались события в Пирл-Харборе, и пароход не смог выйти из гавани или, во всяком случае, не смог взять на борт наших друзей. В результате Ли, который уже пять лет был оторван от научной работы из-за китайско-японской войны, оказался вынужденным ждать еще пять лет, и только после дня победы над Японией нам удалось добиться его возвращения в Соединенные Штаты. В течение всего этого времени место, которое предназначалось ему на кафедре электротехники МТИ, оставалось свободным или полусвободным; когда Ли в конце концов приехал в Америку, он сразу получил должность преподавателя. Вскоре он стал ассистентом, а потом и доцентом.

Положение специалиста, который, наподобие Рип Ван Винкля^*, проспал целое десятилетие и, проснувшись, обнаружил, что мир стал иным, очень трудно.

^* (Герой рассказа американского писателя Вашингтона Ирвинга (1783-1859), проспавший двадцать лет и после этого вернувшийся в родную деревню. )

Первое, что приходит в голову, - потратить один-два года на изучение перемен, происшедших за это время. В каком-то смысле это вполне возможный, хотя далеко не самый правильный путь. Необходимость поглотить огромное количество нового материала может привести к умственному несварению. К тому же тот, кто догоняет, вынужден вступить в соревнование с людьми младшего поколения, которые овладевали определенной отраслью знания по мере ее развития, т. е. более легким путем, и потому чувствуют себя в этой области, как дома. Рип Ван Винклю тягаться с ними не под силу.

Положение Ли облегчалось тем, что я недавно изложил значительную часть статистической теории связи в "Желтой опасности". Беседуя с Ли, я сказал ему, что один из способов не оказаться безнадежно отсталым - это постараться немного забежать вперед, обеспечив себе преимущество в несколько лет и предоставив другим возможность догонять. Ли ухватился за эту идею.

Ему помогли многолетние навыки нашей совместной работы, благодаря которым он прекрасно разбирался в особенностях моей манеры мышления и изложения. Вот почему Ли взял на себя задачу, исходя из набросанных мной (в весьма общем виде) идей, детально разобрать все проблемы, представляющие интерес для инженеров-связистов, т. е. познакомить широкие технические круги с той областью знания, которую я позже назвал кибернетикой.

Ли упорно проводил в жизнь свою программу и за несколько лет добился блестящего успеха. Сейчас он пишет книгу для инженеров, в которой теория связи рассматривается с новой точки зрения^*; в своей работе он проявляет огромное терпение, исключительную тщательность и полное понимание интересов читателя. Так как я слишком близок к появлению на свет этой теории, для меня подобная объективность изложения была бы невозможна.

^* ( Книга Ли под названием "Статистическая теория связи" ("Statistical theory of communication") была опубликована в США в 1960 г.)

Ли познакомил с новыми идеями сотрудников многих государственных и частных лабораторий. Он научил целое поколение молодых инженеров-электриков широко пользоваться статистическими соображениями и рассматривать возникающие в их области задачи с пропагандируемой мной точки зрения. Он организовал летние конференции для инженеров, творчески работающих в промышленности связи; приезжая в МТИ, они получали возможность освежить свои знания с позиций кибернетики.

Таким образом, трудности, созданные десятилетней изоляцией, были успешно преодолены. Старт, взятый Ли в области новых методов, позволил ему быстро наверстать упущенное за 1936-1946 годы, а главное, интересующие его специфические проблемы служили великолепной лакмусовой бумажкой, с помощью которой Ли всегда мог определить, до конца ли он разобрался и достаточно ли близко познакомился с исследованиями предыдущего периода. Короче говоря, курс, который был избран в тот момент, когда по окончании войны семья Ли прибыла на южный вокзал Бостона, полностью себя оправдал.

Возвращение Ли в МТИ очень помогло мне продвинуться в исследовании следящих систем и всего того круга проблем, которому я позднее дал название кибернетики. Как я уже говорил, Ли сейчас сам кончает книгу на эту же тему.

К сожалению, всего того, что могли сделать мы вдвоем, и того, что могли бы сделать на нашем месте сто человек, все равно было бы недостаточно, чтобы охватить хотя бы ничтожную часть литературы по следящим системам и заводам-автоматам, к созданию которых привели наши ранние совместные работы. Заводы-автоматы обещают стать не исключением, а правилом уже для тех, кто занимается сейчас в колледжах. Они породили новый вид специалистов, которые умеют не только строить такие заводы, но и решать с их помощью самые разнообразные задачи. Современная техника создания заводов-автоматов выходит далеко за рамки возможностей сугубого теоретика вроде меня.

Как читатель увидит из следующей главы, я считал своей обязанностью не столько дальнейшее совершенствование заводов-автоматов, сколько объяснение их природы и тех последствий, к которым приведет их распространение; я хотел прежде всего предупредить рабочих и работодателей о необходимости разумного отношения к этой проблеме.