5. Некоторые математические проблемы, связанные с биологическими исследованиями

До сих пор мы все время говорили о возможностях и перспективах применения математических методов для нужд биологии. Но не менее важна и «обратная связь» - влияние биологических исследований на развитие математики, на возникновение новых математических проблем. За последние десятилетия это влияние биологии на математическую проблематику стало достаточно существенным. В этом заключительном разделе нашего краткого очерка мы рассмотрим некоторые математические проблемы, возникшие полностью или в значительной мере в связи с теми или иными биологическими исследованиями.

1. Проблемы надежности и скорости

Одно из замечательных свойств живых систем - это их надежность. Еще сравнительно недавно старые кадровые артиллеристы, сетуя на замену в артиллерии конной тяги механической, выдвигали в качестве основного аргумента то, что живое существо - лошадь - гораздо надежнее в работе, чем самый совершенный механизм. Вместе с тем элементы, из которых строится живая система,- отдельные клетки - вовсе не обладают такой уж большой надежностью. Их ответы на те или иные воздействия довольно неустойчивы, а сами клетки легко разрушаются. Это положение обратно тому, с которым мы обычно встречаемся в технических системах. Там, как правило, усложнение конструкции требует для обеспечения работоспособности системы все большей надежности отдельных ее элементов. Например, если в радиоприемнике имеется пять ламп, каждая из которых служит в среднем 1000 часов, то такое устройство можно считать достаточно надежным. А если взять ламповую вычислительную машину (в настоящее время такие машины почти совсем вышли из употребления, но в 50-х годах они были широко распространены), содержащую несколько тысяч ламп, то при той же надежности этих элементов машина в целом весьма ненадежна, поскольку в среднем через каждые 10-15 минут какая-то из ламп в машине перегорает, а при этом машина выходит из строя.

Какими же способами в живых организмах достигается такая надежность системы, которая существенно превосходит надежность составляющих ее элементов? Как математическая проблема этот вопрос впервые был рассмотрен Дж. Нейманом. Изучая сети, составленные из элементов, каждый из которых может с некоторой вероятностью «не сработать», он показал, что вероятность «несрабатывания» такой сети в целом можно, при соответствующей оранизации ее работы, сделать сколь угодно малой. Например, если имеется достаточно большой запас ненадежных выключателей, каждый из которых с некоторой вероятностью ε^* не замыкает сеть в положении «включено» и с той же вероятностью не размыкает ее в положении «выключено», то из них можно собрать схему, которая будет работать как выключатель, имеющий сколь угодно малую вероятность ошибки.

^* (При этом следует полагать, что ε<½, так как если ε>½, то это просто означает, что положения «включено» и «выключено» нужно поменять местами, а при ε=½ изменение положения выключателя вообще не играет никакой роли и из таких выключателей ничего разумного собрать нельзя)

В такого рода схемах надежность достигается применением процедуры, аналогичной «принятию решения большинством голосов». При этом, однако, увеличение надежности достигается за счет возрастания числа элементов, составляющих сеть. По-видимому, нет достаточных оснований считать, что принципы, найденные Дж. Нейманом для построения надежных схем из ненадежных элементов,- единственные, с помощью которых может быть решена задача обеспечения надежности, и что именно так она решается в живых системах. Таким образом, вопрос о тех общих принципах, которые обеспечивают надежность живых систем, еще далеко не решен.

Проблема надежности, о которой мы упомянули, родственна в известной мере другой проблеме, которую можно назвать проблемой скорости. Как известно, современная вычислительная машина производит арифметические операции со скоростью несравненно большей, чем человек. Тем не менее при решении некоторых задач человеческий мозг вполне может конкурировать по скорости с самой быстродействующей машиной. Предположим, человеку задается вопрос: «Смотрели ли Вы вчера в телескоп?». Как правило, для ответа на этот вопрос человеку достаточно доли секунды. (Может быть, лишь астроном-наблюдатель, для которого смотреть в телескоп - обычное, но все же не ежедневное занятие, задумается на больший срок). При этом человек вовсе не должен вспоминать в деталях весь свой вчерашний день (встал, умылся, позавтракал и т. д.), чтобы дать верный ответ. Он сразу же использует некоторую более общую информацию (например: «никогда в жизни не смотрел в телескоп» или: «смотрел, но это было очень давно»). А для машины нет аналогичных способов быстрого получения ответа. Если мы хотим выяснить, не записана ли в ее памяти (неизвестно, в каком месте) какая-либо определенная информация, то у нас нет иного способа, как перебрать по очереди все ячейки ее памяти. Обследование каждой отдельной ячейки делается быстро, однако при большом объеме памяти весь процесс такого последовательного поиска займет немало времени.

С тем обстоятельством, что человеческий мозг успешно справляется с задачами, требующими, казалось бы, перебора столь большого числа вариантов, что это затруднительно даже для электронной машины, мы сталкиваемся в самых разнообразных случаях, например при игре в шахматы. Хороший шахматист «видит» все возможности игры на несколько ходов вперед и безошибочно рассчитывает многоходовые комбинации, учитывая все возможные варианты. Как показывает несложный подсчет, если при этом действительно перебирать все допустимые правилами игры собственные ходы и все возможные ответы противника, то такой перебор окажется непосильным даже для самых быстрых электронных машин. Высказываемое иногда предположение, что в мозгу на самом деле происходит весьма быстрая, но не контролируемая нашим сознанием переработка информации, представляется маловероятным, так как для этого нужно было бы предположить существование в нервных клетках каких-то неизвестных нам и необычайно быстрых физико-химических процессов (ведь обработка информации - обязательно материальный процесс). Следовательно, экономия времени в такого рода ситуациях достигается не за счет каких-либо сверхбыстрых процессов, а за счет применения методов обработки информации, существенно отличных от полного перебора. В последнее время в связи с развитием так называемого эвристического программирования, т. е. применения вычислительных машин к решению разного рода невычислительных задач (сюда относится и составление программ для игры в шахматы), был выполнен ряд исследований, посвященных различным методам, повышающим эффективность перебора возможных вариантов с целью выбора наилучшего. Полученные при этом математические результаты позволили, например, реализовать на сравнительно медленной вычислительной машине М-20 такую программу для игры в шахматы, которая для каждого хода проделывает анализ на 5 полуходов вперед (т. е. оценивает положение, возникающее после трех собственных ходов и двух ответов противника). Такую программу на машине М-20(да и на более быстродействующей) заведомо невозможно реализовать, если пользоваться лишь методом полного перебора всех возможных вариантов.

Математические результаты, относящиеся к исследованию наиболее эффективных методов обработки и использования больших массивов информации, представляют существенный интерес. Однако то, что сделано в этом направлении до сих пор, не дает еще достаточно ясного ответа на вопрос о том, как справляются с такого рода задачами живые системы. Таким образом, наряду с парадоксом о надежных системах, построенных из ненадежных элементов, живые организмы приводят нас еще к одному парадоксу, который можно сформулировать так: быстрые системы, построенные из медленных элементов.

2. Автоматы в случайных средах

Одно из важных качеств живых систем состоит в том, что можно назвать целесообразностью их поведения. Каждое живое существо действует так, чтобы обеспечить себе возможно более благоприятные условия (ищет пищу, уклоняется от опасности и т. д.). Естественно, возникает желание построить формальную математическую модель того, что мы называем целесообразностью поведения. Это было осуществлено M. Л. Цетлиным в развитой им теории поведения автоматов в случайных средах. Попытаемся кратко изложить основные идеи этой теории.

Под автоматом, или, точнее, конечным автоматом, понимается некоторое устройство А, обладающее следующими свойствами:

1.Это устройство имеет некоторое фиксированное число состояний s₁, s₂,.., s_n. В каждый момент времени автомат находится в одном из этих состояний;

2.Автомат может производить некоторое число действий φ₁, φ₂,.., φ_ι; выбор действия определяется состоянием автомата;

3.Автомат может получать от внешней среды некоторое число различных сигналов f₁, f₂, .., f_k и в зависимости от получаемого сигнала менять свое состояние.

Рассмотрим тот простейший случай, когда входной сигнал, получаемый автоматом от внешней среды, принимает только два значения: f=1 и f=0, которые мы условно назовем «поощрением» и «штрафом» (или «отсутствием поощрения»).

Мы скажем, что автомат А находится в стационарной случайной среде, если действия автомата и сигналы, получаемые им от внешней среды, связаны следующим образом: в ответ на действие φ_α, совершаемое в момент времени t, автомат в момент t+1 с вероятностью р_α получает поощрение, а с вероятностью q=1-р_α получает штраф^*. Если автомат совершает все свои действия с одной и той же вероятностью и независимо от воздействия среды, то математическое ожидание его выигрыша (за один такт работы) равно

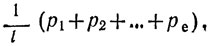
где l - число действий. Далее очевидно, что при любом поведении автомата математическое ожидание его выигрыша заключено между minр_α (что соответствует непрерывному ?повторению самого невыгодного действия) и maxpр_α (что отвечает ? наивыгоднейшему действию). Если бы вместо автомата действовал человек, который знал бы величины р_α, то его тактика была бы очевидна: он все время повторял бы то действие, которому отвечает максимальное р_α, и получал бы (в среднем) максимальный возможный выигрыш, равный maxр_α. Но мы рассматриваем не человека, а автомат, который такими сведениями не располагает, а может лишь в зависимости от получаемых от среды сигналов переходить из одного состояния в другое и, следовательно, менять свои действия. То, как автомат меняет свои состояния (а следовательно, и действия) в ответ на сигналы среды, называется тактикой автомата. Мы скажем, что автомат обладает целесообразной тактикой, если математическое ожидание его выигрыша больше, чем ¹/_l (р₁+р₂ +... + P_l), т. е. больше, чем выигрыш, отвечающий чисто случайному поведению. Нетрудно указать примеры автоматов, обладающих целесообразным поведением. Более того, можно доказать следующее утверждение: если среда (т. е. вероятности р_α) задана, то для каждого положительного числа ε можно построить такой автомат, что математическое ожидание его выигрыша будет меньше, чем на ε отличаться от max р_α, т. е. от максимально возможного выигрыша.

^* (Величины р_α и q_αзависят от состояния автомата, но не зависят от момента времени t. В этом и состоит смысл термина «стационарная» среда. Время мы здесь для удобства считаем не непрерывным, а дискретным)

Приведем элементарный пример автомата, обладающего целесообразным поведением. Пусть автомат А_2,2 имеет два состояния s₁ и s₂ и два действия (φ₁ и _φ2, причем в состоянии s₁ совершается действие φ₁, а в состоянии s₂ - действие φ₂. Пусть тактика этого автомата состоит в том, что при получении поощрения она сохраняет свое состояние, а при штрафе - меняет. Если в соответствии с введенными выше обозначениями р₁ и q₁=1-p₁ - вероятности поощрения и штрафа в первом состоянии, а р₂ и q₂=1-р₂ - аналогичные вероятности для второго состояния, то, как нетрудно показать, наш автомат (независимо от своего состояния в начальный момент) будет на протяжении длительного промежутка времени с вероятностью

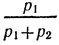
находиться в состоянии s₁, а с вероятностью

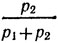
в состоянии s₂. Так как в состоянии s_i (i=1,2) математическое ожидание выигрыша равно то окончательно математическое ожидание выигрыша для нашего автомата равно

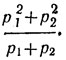
Предположим, что р₁≠р₂ (если p₁ = p₂, то все тактики автомата дают один и тот же результат). Тогда элементарный подсчет показывает, что

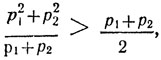
т. е. наш автомат выигрывает больше, чем автомат, выбирающий свои действия случайно.

Если параметры среды (т. е. вероятности р_α ) не постоянны, а меняются с течением времени случайным образом, то опять-таки можно ставить вопрос об автомате, обладающем в данной среде целесообразным поведением. Можно, например, считать, что имеются две стационарные среды и автомат случайным образом переходит из одной среды в другую. При этом ему нужно после каждого перехода «адаптироваться к новым условиям», и важно, чтобы это время адаптации было мало по сравнению со временем, в течение которого среда остается постоянной. Иначе автомат не будет успевать приспосабливаться к перемене условий существования.

Вместо взаимодействия одного автомата со средой можно рассматривать поведение коллектива взаимодействующих между собой автоматов в некоторой среде. При этом возможный выигрыш каждого автомата определяется как его собственной тактикой, так и тактикой остальных автоматов, которые по отношению к каждому фиксированному автомату тоже играют роль своего рода «внешней среды».

Мы не имеем возможности излагать здесь теорию поведения автоматов сколько-нибудь подробно. Нам хочется лишь подчеркнуть, что такое, казалось бы, далекое от математики понятие, как понятие целесообразности поведения живого организма, на самом деле, при соответствующей его формализации, приводит к постановке точных задач и к интересным и важным математическим результатам.

3. «Метод оврагов»

Задача о «разумном» или «целесообразном» функционировании той или иной системы, биологической или технической, родственна, По существу, чисто математической задаче об отыскании экстремума (для определенности, скажем, минимума) некоторой функции многих переменных. Действительно, обычно можно бывает связать с системой некоторую функцию Φ (оценочную функцию) так, чтобы ее минимум отвечал тому состоянию системы, которое с некоторой точки зрения является оптимальным.

Если бы оценочная функция, о которой идет речь, была задана какой-то формулой, то для нахождения ее минимума можно было бы воспользоваться хорошо известным из анализа приемом: продифференцировать эту функцию по каждому из аргументов, приравнять эти производные нулю и решить полученную таким образом систему уравнений^*. Однако в задачах, связанных с физиологией, мы обычно не можем дать аналитического выражения для оценочной функции. Поэтому поиск ее минимума должен, по необходимости, сводиться к серии проб, или чисто случайных, или подчиненных определенной тактике. Так как наша оценочная функция, вообще говоря, меняется со временем (то состояние, которое благоприятно для системы в данный момент, может оказаться непригодным для нее в дальнейшем в силу изменения окружающих условий), то процесс отыскания ее минимума должен повторяться многократно и не быть слишком длительным (иначе существенное изменение ситуации произойдет раньше, чем мы закончим поиск). Какие же возможны разумные тактики такого поиска?

^* (Впрочем, при большом числе переменных этот путь мало эффективен и в том случае, если функция задана аналитически)

Если о функции Φ = Φ(х₁ х₂, .., х_n) нам ничего не известно, то для отыскания ее минимума нельзя предложить ничего лучшего, чем так называемый слепой поиск, состоящий в том, что различные точки в пространстве параметров просматриваются в том или ином случайном порядке. В каждой из выбираемых точек находится значение оценочной функции и поиск прекращается тогда, когда находится значение, не превосходящее некоторого допустимого предела. После того как, в силу изменения оценочной функции во времени, ее значение в данной точке превысит допустимый предел, поиск возобновляется. Ясно, что такой поиск, особенно в случае большого числа параметров, может быть весьма продолжительным. Например, если бы человек обучался координации движений при ходьбе с помощью «слепого поиска», то скорее всего он не научился бы ходить до конца жизни.

Если оценочную функцию можно считать непрерывно зависящей от параметров, то для отыскания ее минимума можно применять различные методы локального поиска, общей основой которых служит следующая идея: изучив поведение функции в окрестности некоторой точки, мы устанавливаем, в каких направлениях функция убывает, и в соответствии с этим перемещаемся в новую точку. Например, определяем в данной точке направление наибыстрейшего убывания функции и затем сдвигаемся в этом направлении на определенное расстояние (так называемый «градиентный метод»). Однако во всех таких процессах локального поиска существует опасность «зацикливания», т. е. блуждания в окрестности какой-то локальной «ямы», в которой значения функции меньше, чем в близлежащих точках, но весьма далеки от абсолютного минимума.

Опасность такого зацикливания делает существенным использование тех или иных методов нелокального поиска. Однако для того чтобы получить на этом пути результаты, существенно лучшие, чем слепой поиск, нужно, чтобы наша функция была соответствующим образом организована. Поясним смысл этого, рассмотрев так называемый «метод оврагов», предложенный для отыскания экстремумов функций многих переменных И. М. Гельфандом и М. Л. Цетлиным. Идея этого метода возникла на основе изучения особенностей поведения живых систем.

Предположим, что переменные, от которых зависит функция Φ, могут быть разбиты на две группы, скажем х_n, х₂, .., х_n и у₁ у₂,.., у_k. Допустим, что большинство переменных входит в первую группу и что изменение значений этих параметров заметно меняет значение функции Φ. Эти переменные мы назовем несущественными. Вторая группа включает небольшое число переменных (может быть, всего 2-3) и от них функция Φ зависит сравнительно слабо. Эти переменные называются существенными. То обстоятельство, что изменение несущественных переменных достаточно резко сказывается на значении оценочной функции, позволяет сравнительно просто подобрать подходящие значения этих переменных; поэтому основные затруднения при отыскании экстремума связаны с наличием существенных переменных (именно этим и объясняется та на первый взгляд несколько нелогичная терминология, которую мы ввели). Конечно, не всякая функция многих переменных допускает такое разбиение параметров на существенные и несущественные. Однако для многих функций, возникающих из практических задач, такое положение имеет место. В частности, с такой ситуацией приходится встречаться в задачах координации движений. Грубая схема того или иного движения (бег, прыжок, плавание, удар ракеткой по мячу и т. д.) усваивается человеком, как правило, сравнительно легко (на нашем языке - легко находятся нужные значения «грубых», несущественных параметров этого движения), после чего начинается трудная и кропотливая «отработка техники», совершенствование деталей этого движения (т. е. выбор оптимальных значений существенных параметров).

Разумеется, и в тех случаях, когда рассматриваемая функция обладает «организацией» в указанном выше смысле, мы не можем заранее выделить существенные и несущественные параметры, а лишь исходим из возможности такого выделения. Само же выделение существенных и несущественных переменных должно происходить автоматически, в процессе отыскания экстремума.

Таковы те общие соображения, которые были положены в основу «метода оврагов». Сам этот метод состоит в следующем. Сперва в пространстве переменных выбираем некоторую произвольную точку Хо и, отправляясь от нее, начинаем поиск минимума каким-либо локальным способом, например спуском по градиенту. Спуск продолжается до тех пор, пока дальнейшее продвижение не станет малоэффективным, т. е. пока отношение Δ/Φ Φ(где ΔΦ - изменение Φ за один шаг) не станет меньше некоторой заданной величины Δ. Величину Δ не надо брать слишком малой, так как там, где ΔΦ/Φ мало, различие между существенными и несущественными переменными исчезает и применение локального спуска приводит к блужданию, не приближающему нас к цели.

Пусть локальный спуск привел нас в некоторую точку М₀. Зафиксируем ее и выберем некоторую точку Х₁ в окрестности исходной точки Х₀, по отстоящую от X₀ на расстояние, существенно превышающее шаг градиентного спуска. Применив в точке Х₁ локальный спуск, придем в некоторую точку М₁. После этого соединяем точки М₀ и М₁ прямой, выбираем на этой прямой точку Х₂, отстоящую от точки M₀ на некоторое расстояние L, существенно превышающее первоначально выбранный градиентный шаг, и затем с шагом L производим из Х₂ спуск, приводящий нас в некоторую точку М₂. Далее, по точкам M₁ и М₂ выбирается точка Х₃ так же как по М₀ и M₁ выбиралась точка Х₂, и процесс повторяется.

Наглядный смысл метода состоит в следующем. Разделение переменных на существенные и несущественные означает, что поверхность, определяемая рассматриваемой функцией Φ, имеет вид рельефа, прорезанного «оврагами», и мы сперва нащупываем направление такого «оврага» (прямая М₀М₁), а потом идем по дну этого оврага к возможно более низкой точке (см. рис. 5).

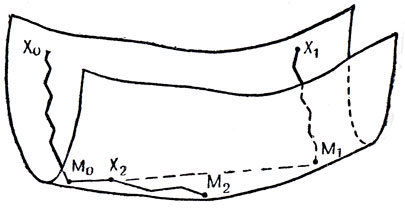
Рис. 5 Схема «метода оврагов»,

«Метод оврагов» был с успехом применен к решению ряда задач, например к изучению молекулярной структуры некоторых аминокислот по данным рентгеноструктурного анализа.

4. Формальные модели самовоспроизведения

Во все времена одной из самых характерных черт живых существ считалась их способность к порождению себе подобных. Вопрос о том, способны ли к такому воспроизведению не живые существа, а машины, представляется на первый взгляд не очень серьезным. Дж. Нейман был первым, кто поставил его как строгую научную проблему и получил здесь глубокие результаты. Его интерес к этим вопросам стимулировался как желанием разобраться в фундаментальных свойствах биологических систем, так и стремлением выяснить те возможности, которыми обладают (хотя бы в принципе) создаваемые человеком автоматические конструкции.

Некоторыми авторами, в том числе и самим Дж, Нейманом, были предложены различные физические конструкции, обладающие способностью к самовоспроизведению. Точнее, речь идет о следующем: некоторое устройство, «машину», помещают в среду, в которой находятся в достаточном количестве соответствующие детали («пища»). Машина отбирает необходимые детали и создает из них собственную копию. В отсутствие же первоначальной машины, т. е. «родителя», детали «сами собой» в такую машину не соединяются.

Некоторые из таких конструкций весьма остроумны. Так, например, Пенроуз придумал следующую модель: весь запас деталей состоит из двух типов плоских кусков твердого материала, снабженных выступами и захватами. Обозначим эти два типа деталей символами А и В. Элементы А и В могут сцепиться друг с другом двумя различными способами, образуя либо машину АВ, либо машину ВА. Если в закрытый ящик поместить машину АВ и запас элементов обоих типов, то при встряхивании ящика в нем (за счет сил сцепления и силы тяжести) будут возникать новые копии машины АВ (но не ВА). Если же первоначально в ящик поместить машину ВА и запас деталей, то при встряхивании будут возникать новые экземпляры машины ВА (но не АВ).

Построение подобных моделей весьма увлекательно, но мы рассмотрим сейчас чисто логическую сторону дела, т. е. будем интересоваться не физическими, а математическими моделями самовоспроизведения.

Представим себе плоскость, разбитую на квадратные клетки. Предположим, что в каждой такой клетке «живет» некий автомат, имеющий конечное число состояний. Время будем считать дискретным. Предположим, что состояние каждого автомата в момент времени Т определяется состоянием самого этого автомата и всех его соседей в момент Т-1 Будем, наконец, считать, что для каждого автомата есть состояние, называемое покоем, и что в каждый момент времени все автоматы, кроме конечного их числа, находятся в этом состоянии.

Назовем конфигурацией любой фиксированный набор клеток, в каждой из которых для находящегося в ней автомата зафиксировано его состояние. Конфигурация С′ называется копией конфигурации С, если одна из них может быть переведена в другую с помощью некоторого движения плоскости. Пусть С - некоторая конфигурация и пусть в момент Т=0 во всех клетках, не принадлежащих С, автоматы находятся в состоянии покоя. Говорят, что эта конфигурация способна произвести n потомков за время Т, если в какой-то момент Т′≤Т в конфигурации, состоящей из всех активных (т. е. не находящихся в состоянии покоя) клеток, имеется n попарно непересекающихся копий конфигурации С. Конфигурация называется неограниченно размножающейся, если для каждого n найдется время T, за которое эта конфигурация способна воспроизвести n потомков.

Описанная формальная схема представляется, конечно, чрезвычайно упрощенной по сравнению с теми процессами самовоспроизведения, которые мы наблюдаем в живой природе. Однако эта упрощенная схема допускает постановку и строгое математическое решение ряда интересных и важных вопросов, таких, как существование нетривиальных (т. е. достаточно сложных) неограниченно размножающихся конфигураций, оценка возможной скорости их размножения, существование конфигураций, которые можно задать в начальный момент, но которые не могут быть получены в момент Т>0 ни из какой конфигурации, заданной в начальный момент^*, и т. д. Таким образом, здесь мы опять-таки, как и во многих других случаях, исходя из некоторого реального явления (в данном случае - размножения), строим абстрактную модель, сохраняющую лишь некоторые, самые основные черты этого явления, но зато уже достаточно простую, чтобы ее исследование можно было строить как точную математическую теорию.

^* (Конфигурацию, которая не может быть получена ни из какой начальной, называют «конфигурацией райского сада» (по библейским сказаниям, люди начали свое существование в райском саду, но вернуться туда уже не могут.)

5. Проблемы искусственного интеллекта и распознавание образов

До сих пор мы касались, в основном, математических моделей и проблем, возникающих в связи с такими биологическими процессами, как выполнение движений, распространение возбуждения, размножение (самовоспроизведение). Все эти процессы связаны с «животной», а не с «интеллектуальной» активностью. Но в последнее время возник большой интерес к проблемам, которые принято называть проблемами «искусственного интеллекта». Под этим понимается решение, с помощью вычислительных машин и соответствующих программ для них, задач, которые мы считаем специфическими для сознательной деятельности разумного существа. Конечно, выполнение сложных вычислений, с которыми машина справляется несравненно быстрее, чем человек,- это тоже интеллектуальная деятельность, но речь идет не об этом, а о задачах не вычислительного характера. Например, может ли машина «научиться» играть в шахматы хотя бы на уровне рядового шахматиста, а если это возможно, то какие принципы должны быть положены в основу ее обучения? Задача составления и исследования «шахматных программ» уже дала ряд интересных и важных математических результатов, значение которых выходит за пределы шахматной проблематики.

Сейчас делаются уже небезуспешные попытки осуществить на вычислительных машинах такую «высокоинтеллектуальную» деятельность, как нахождение формулировок и доказательств математических теорем. Несомненно, впрочем, что в этой области мы достигли бы значительно больших успехов, если бы сами математики могли разобраться в том, как они справляются с подобной деятельностью. По-видимому, однако, значительная часть такого рода деятельности лежит в какой-то плохо контролируемой подсознательной области.

К проблемам искусственного интеллекта примыкает и так называемое распознавание образов, о котором мы уже упоминали выше в связи с задачей анализа кардиограмм. Будем для определенности говорить о зрительных образах, хотя можно было бы рассматривать и образы какой-либо иной природы (скажем, воспринимаемые с помощью слуха или осязания). Для того чтобы разъяснить сущность такого рода проблем, рассмотрим следующий пример. Допустим, что человеку, не знающему букв, показывают различные начертания разных букв и каждый раз говорят, что это за буква. Вскоре этот человек научится распознавать буквы, причем не только в тех начертаниях, которые он видел, но и в других. Едва ли этот человек смог бы сам точно сформулировать те признаки, по которым он отличает одну букву от другой. Точно так же мы не можем детально описать, как именно (по каким формальным признакам) мы отличаем кошку от собаки, хотя и делаем это достаточно легко и уверенно.

Возникает желание, с одной стороны, проанализировать те методы, с помощью которых задачу узнавания решает человек, а с другой - составить программу, дающую решение такого рода задач на вычислительной машине. Видимо, процесс распознавания образов, осуществляемый нашим мозгом, основан в общих чертах на следующих принципах, которыми мы пользуемся подсознательно. В том материале, который предъявляется для обучения распознавания тех или иных объектов, мы фиксируем различные признаки этих объектов (размер, форма, окраска и т. п.) и отбираем те из них, которые полезны в данной задаче (например, если нужно отличать зайцев от кошек, то число ног - бесполезный признак, поскольку их по четыре и у тех и у других, а длина ушей - полезный признак, поскольку у кошек и у зайцев она сильно различается). Отобрав некоторое, сравнительно небольшое число таких полезных признаков, наш мозг пользуется ими в дальнейшем для опознавания новых объектов. Важно, что при этом мы не имеем заранее никакого списка «полезных» или, точнее, «несущих информацию» признаков; их отбор происходит в процессе самого обучения. При переходе к новой задаче - распознаванию объектов других типов - отбор этих признаков производится заново.

Описанные принципы могут быть положены в основу составления машинной программы распознавания образов. Однако реализация этих принципов на вычислительной машине связана с рядом математических проблем, в известной мере аналогичных тем, которые возникают, например, при составлении шахматных программ. В частности, здесь мы снова сталкиваемся с уже упоминавшимся парадоксом: мозг, состоящий из медленно работающих нейронов, решает задачи типа распознавания несравненно быстрее, чем быстродействующая вычислительная машина. Например, в экспериментах по узнаванию, проведенных М. М. Бонгардом и его сотрудниками на машине М-20, распознавание буквы «А» занимало около 20 секунд, а человеку для решения подобных и даже значительно более сложных задач распознавания достаточно долей секунды.

Видимо, настанет время, когда математическая биология превратится в такое же мощное орудие исследования живой природы, каким применительно к физическим явлениям служит сейчас теоретическая физика. Вместе с тем несомненно и то, что биологические проблемы послужат источником многих математических исследований. Если пока что эти исследования развиваются не слишком быстро, то это объясняется не недостатком биологических проблем, требующих математической разработки, а сложностью этих проблем. С некоторыми уже полученными в этой области результатами мы постарались познакомить читателя этой маленькой книжки.