171. Головоломный лабиринт

Приведем один не построенный, а только начерченный лабиринт (рис. 192) с готовым и упрощенным решением его: все тупики (слепые проходы) в нем уже заштрихованы, и главнейшие пути указаны точечными или штриховыми линиями. И по решению, данному на этой фигуре, видно, что от А надо сначала идти к С и потом от F к В.

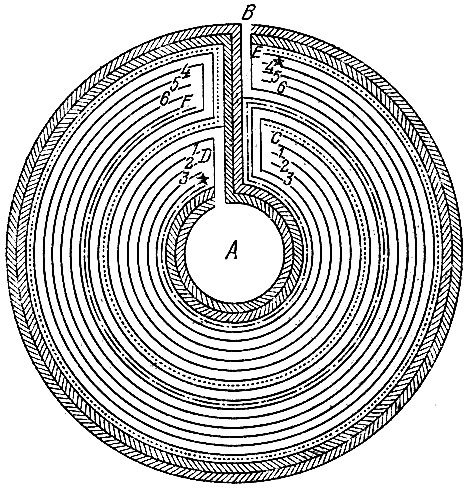
Рис. 192

Но, когда мы придем к С, у нас появляются три дороги, обозначенные 1, 2, 3, чтобы дойти до D. Точно так же, когда мы дойдем до F, тоже видны три дороги, обозначенные 4, 5, 6, чтобы дойти до F. У нас есть также обозначенная точками дорога от С до Е, другая - обозначенная точками дорога от D до F и проход от D до E, указанный звездами. Мы можем, следовательно, выразить положение дела маленькой упрощенной диаграммой на рис. 193. Здесь все пути соответствуют путям кругообразного лабиринта, но только более доступны глазу. И вот при таких-то условиях, при условии также, которое здесь можно выполнить, не проходить дважды через один и тот же проход, окажется 640 путей от А до В.

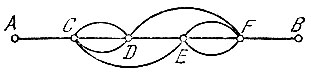
Рис. 193

Для головоломного лабиринта это - не правда ли?- довольно хорошо.