170. О фигурах, вычерчиваемых одним росчерком

Известен анекдот: некто давал миллион рублей каждому, кто начертит следующую фигуру (рис. 180). Но при вычерчивании ставилось одно условие. Требовалось, чтобы фигура эта была вычерчена одним непрерывным росчерком, т. е. не отнимая пера или карандаша от бумаги и не удваивая ни одной линии, другими словами, по раз проведенной линии нельзя уже было пройти второй раз.

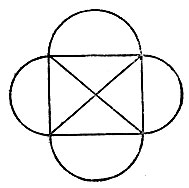
Рис. 180

Надежда стать "миллионером", решив такую легкую задачу, может заставить испортить много бумаги и потратить много времени на попытки вычертить эту фигуру, как требовалось, одним росчерком. Задача, однако, не решается, и это тем досаднее, что она не решается только "чуть-чуть"... Никак не удается провести только одной "последней" какой-либо линии. Удается даже открыть секрет, что вся трудность в том, чтобы вычертить сначала одним росчерком, не повторяя линии, еще более простую фигуру - четырехугольник с двумя диагоналями (рис. 181). Это, казалось бы, уже совсем просто, а все-таки... не удается!...

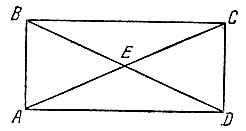
Рис. 181

Сомнения в невозможности решения этой задачи все-таки остаются, тем более что фигуры, гораздо более сложные и трудные с виду, легко вычерчиваются одним росчерком. Так, например, выпуклый пятиугольник со всеми его диагоналями легко вычерчивается одним непрерывным движением без повторения, причем получается фигура, представленная на рис. 182.

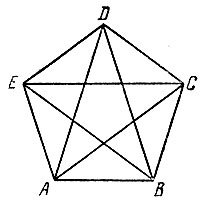
Рис. 182

То же самое легко удается со всяким многоугольником с нечетным числом сторон и никак не удается с квадратом, шестиугольником и т. д. - словом, с многоугольником с четным числом сторон.

Теперь нам нетрудно будет разобраться и показать, какую из любых данных фигур можно вычертить одним росчерком, без повторения линий, а какую нет. Каждую из задач подобного рода можно свести к разобранной уже нами Эйлеровой задаче о мостах.

В самом деле, возьмем, например, четырехугольник ABCD с двумя его диагоналями, пересекающимися в Е (рис. 181). Можно ли его вычертить одним непрерывным росчерком, без повторения линий?

Точки А, В, С, D и Е мы представим себе как центры некоторых местностей, разделенных рекой, а линии, соединяющие эти точки, - как мосты, ведущие в эти местности. Что же в данном случае получаем? Пять местностей, из которых четыре нечетные и одна четная. Мы знаем уже, что в таком случае нельзя за один раз обойти все мосты, не переходя ни через один два раза, или, другими словами, нельзя обойти все данные точки одной непрерывной линией без повторения прежнего пути.

Случаи возможности и невозможности вычерчивания одним росчерком фигур совершенно те же, что и в задаче о мостах. Одна задача, в сущности, сводится к другой.

Всякий нечетный многоугольник со всеми его диагоналями можно вычертить одним росчерком без повторения линий потому, что этот случай соответствует тому, когда данные в задаче о мостах местности все четные.

Соображения, изложенные здесь, одинаково прилагаются ко всякой фигуре, образована ли она прямыми или кривыми линиями, на плоскости или в пространстве. Так, нетрудно видеть, что можно описать одним непрерывным движением все ребра правильного октаэдра и нельзя этого сделать для четырех остальных правильных выпуклых тел.

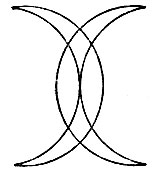
Рис. 183

Говорят, что Магомет вместо подписи (он был неграмотен) описывал одним росчерком состоящий из двух рогов Луны знак, представленный на рис. 183. И это понятно, потому что в данном случае мы имеем дело только с точками четного порядка, а следовательно, вычертить такую фигуру одним росчерком без повторения тех же линий всегда можно. Всегда можно также вычертить одним росчерком и такую Фигуру, где, помимо точек четного порядка, есть и две точки (но не более) нечетного порядка. Весьма красивый и замысловатый образчик такой фигуры, заключающий в себе две нечетные точки А и Z, показан на рис. 184. С какой-нибудь из этих точек и надо начинать непрерывное вычерчивание фигуры, как мы уже знаем из задачи о мостах.

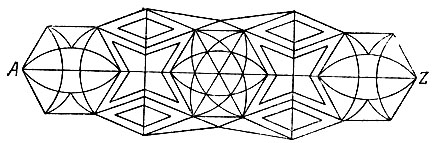
Рис. 184

Также нельзя вычертить одним росчерком фигуры на рис. 185 и 186 при всей их видимой простоте, так как в первой восемь, а во второй - двенадцать точек нечетного порядка. Первая может быть вычерчена не менее как четырехкратной, т. е. состоящей из четырех непрерывных кусков, а вторая - не менее как шестикратной линией.

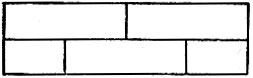
Рис. 185

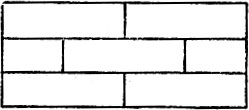
Рис. 186

Если взять шахматную доску с 64 клетками, то в ней - 28 точек нечетного порядка, и, чтобы вычертить ее, надо чертить 14-кратную линию. С другой стороны, если взять треугольник, поделить каждую из его сторон на 12 (или сколько угодно) равных частей и провести из точек деления линии, параллельные другим сторонам, то полученная сетчатая фигура может быть вычерчена одним непрерывным движением без повторений. Таких примеров можно подобрать сколько угодно.

Для упражнения предлагаем читателю заняться во время досуга вычерчиванием с одного росчерка фигур, приведенных на рис. 187.

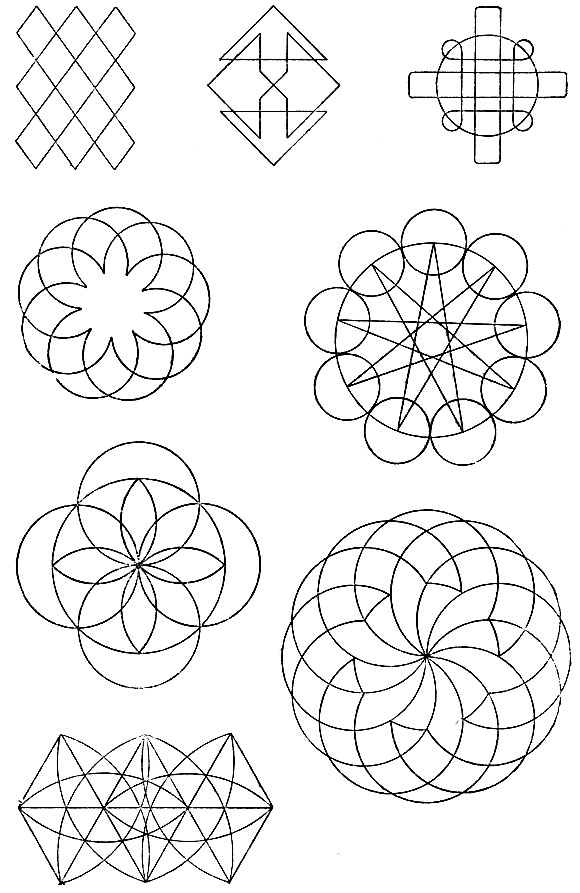
Рис. 187