167. Задача Эйлера

Задача, предложенная Эйлером в 1759 году, заключается в следующем.

Река, огибающая остров, делится на два рукава, через которые переброшено семь мостов: а, b, с, d, f, g (рис. 177). Спрашивается, можно ли совершить такую прогулку, чтобы за один раз перейти через все эти мосты, не переходя ни через один мост два или более раз?

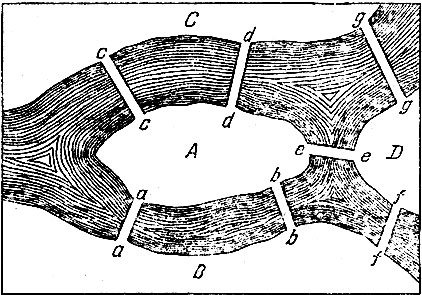
Рис. 177

- Это вполне возможно!- скажет кто-нибудь.

- Нет, это невозможно!- скажет другой. Но кто прав и кто нет и как это доказать? Самый простой путь решения задачи, казалось бы, такой: сделать все возможные пробы таких переходов, т.е. перечислить все возможные пути, и затем рассмотреть, какой или какие из них удовлетворяют условиям вопроса. Но очевидно, что даже в случае только семи мостов приходится делать слишком много таких проб. А при увеличении числа мостов такой способ решения практически совершенно немыслим. Да, кроме того, при одном и том же числе мостов задача изменяется в зависимости еще от расположения этих мостов. Поэтому изберем иной, более надежный путь решения задачи.

Решение. Прежде всего исследуем, возможен или нет искомый нами путь для данного расположения семи мостов. Для облегчения рассуждений введем такие условные обозначения:

Пусть А, В, С и D будут разные части суши, разделенной рукавами реки (рис. 177).

Затем, переход из места Л в место В мы будем обозначать через АВ - все равно, по какому бы мосту мы ни шли, по а или по b. Если затем из В мы перейдем в D, то этот путь обозначим через BD, а весь переход, или путь из А в D, обозначим через ABD, так что здесь В одновременно обозначает и место прибытия и место отправления.

Если теперь из D перейдем в С, то весь пройденный путь обозначим через ABDC. Итак, это обозначение из четырех букв показывает, что из места А мы, пройдя места В и D, пришли в С, причем перешли три моста.

Значит, если мы перейдем четвертый мост, то для обозначения пути нам понадобится пять букв. После перехода следующего, пятого моста понадобится обозначить пройденный путь шестью буквами и т. д.

Словом, если мы обошли по одному разу все семь данных мостов, то наш путь должен был бы обозначаться восемью буквами (вообще, если есть n мостов, то для обозначения искомого нами пути через эти мосты понадобится n + 1 буква).

Но как и в каком порядке должны идти буквы в этом обозначении?

Между берегами А я В есть два моста. Значит, последовательность букв АВ или ВА должна быть два раза. Точно так же два раза должно повторяться соседство букв А и С (между этими местами тоже два моста). Затем, по одному разу должно быть соседство букв А и D, В и D, D и С.

Следовательно, если предложенная задача разрешима, т. е. можно мосты перейти так, как требуется задачей, то необходимо:

1) чтобы весь путь обозначался восемью буквами; 2) чтобы в расположении этих букв соблюдались указанные условия относительно соседства и повторяемости букв.

Разберемся теперь в следующем весьма важном обстоятельстве.

Возьмем, например, местность А, соединенную с другими местностями несколькими мостами: а, b, с, ... (в данном случае пятью мостами). Если мы перейдем мост а (все равно откуда, из А или из В), то в обозначении пути буква А появится один раз. Пусть пешеход перешел 3 моста а, b и с, ведущие в А. Тогда в обозначении пройденного пути буква А появится два раза, в чем нетрудно убедиться. Если же на А ведут 5 мостов, то в обозначении пути через все эти мосты буква А повторится 3 раза. Вообще, легко вывести, что если число мостов, ведущих в А, есть нечетное, то, чтобы узнать, сколько раз в обозначении требуемого пути повторится буква А, надо к этому нечетному числу мостов прибавить единицу и полученное число разделить пополам. То же, конечно, относится и ко всякой иной местности с нечетным числом мостов, которую для краткости будем называть нечетной местностью.

Усвоив все предыдущее, приступим к окончательному исследованию задачи Эйлера.

В местность А ведет пять мостов. В каждую из местностей В, С и D ведет по три моста. Значит, все эти местности нечетные, и на основании только что сказанного в обозначение полного пути через все семь мостов необходимо, чтобы

Получается, таким образом, что в обозначение искомого пути обязательно должно войти 9 букв. Но мы уже доказали выше, что в случае возможности решения задачи весь путь должен обозначаться только восемью буквами. Итак, задача для данного расположения семи мостов неразрешима.

Значит ли это, что задача о переходе по одному разу через мосты неразрешима всегда, когда имеется один остров, два рукава реки и семь мостов? Конечно нет. Доказано только, что задача неразрешима для данного расположения мостов. При ином расположении этих мостов и решение могло бы быть иное.

Теперь же заметим, что во всех тех случаях, когда число мостов, ведущих в различные места, нечетное, можно применять рассуждения, совершенно аналогичные предыдущим, и, таким образом, убедиться в возможности или невозможности решения задачи. И нетрудно вывести для данного случая такое общее правило:

Если число букв, которые должны входить в обозначение полного пути перехода через все мосты по одному разу, не равно числу мостов, увеличенному на единицу, то задача неразрешима.

Для этого же случая "нечетных местностей" заметим и то, что правило для нахождения числа повторений какой-либо буквы, например А, в обозначении полного пути всегда одинаково приложимо, будут ли ведущие из А мосты вести в одно какое-нибудь место В или же в различные места.

Чтобы перейти к более общему решению задачи, необходимо рассмотреть случаи, когда имеется четное число мостов, ведущих откуда-нибудь в другие места.

Пусть, например, из места А переброшено через реку четное число мостов. Тогда при обозначении пути перехода через все мосты по одному разу надо различать два случая: 1) начинается ли путь из А или 2) из другого места.

В самом деле, если из А в В, например, ведут два моста (рис. 178), то путник, отправившийся из А и прошедший по одному разу оба моста, должен свой путь обозначать так: АБА, т. е. буква А повторяется два раза. Если же путник пройдет через те же два моста, но из места В, то буква А появится всего один раз, ибо этот путь обозначится через ВАВ.

Рис. 178

Предположим теперь, что в А ведут четыре моста,- из одной ли местности или из разных, это все равно. И пусть путник отправляется в обход по одному разу всех мостов из места А. Опять легко видеть, что в таком случае при обозначении пройденного пути буква А повторяется три раза; но если начать обход из другой местности, то буква А повторится только два раза. Точно так же в случае шести мостов буква А в обозначении всего пути повторится четыре раза или три, смотря по тому, начался ли переход из А или из другой местности. Словом, можно вывести такое правило:

Если число мостов известной местности четное (четная местность), то в соответствующем обозначении пути буква, обозначающая местность, появляется число раз, равное половине числа мостов, если переход начался из другой местности. Если же переход начался из самой четной местности, то число появлений этой буквы равно половине числа мостов плюс единица.

Очевидно, однако, что при полном пути переход начинается из одной только какой-нибудь определенной местности. Поэтому условимся раз навсегда для четной местности число повторений ее букв в обозначении пути считать равным половине числа мостов, ведущих в эту местность, а для нечетной местности число повторений ее букв получим, если к числу мостов этой местности прибавим единицу и полученный результат разделим пополам. Итак, при решении задачи о мостах необходима различать два случая:

В первом случае число повторений букв, обозначающих полный путь, должно быть равным числу мостов, увеличенному на единицу, иначе задача неразрешима.

Во втором случае полное число повторений букв должно равняться числу мостов, так как, начиная путь с четной местности, нужно число повторений соответствующей буквы увеличить на единицу только для одной местности.

Общее решение. Рассмотрим теперь задачу о мостах с более общей точки зрения. Из предыдущих рассуждений мы уже можем вывести общий прием решения каждой подобной задачи о мостах. Во всяком случае мы можем сразу убедиться в невозможности подобного решения. Для этого расположим лишь решение так:

1. Отмечаем общее количество мостов и ставим его в заголовке решения.
2. Обозначаем различные местности, разделенные рекой, буквами А, В, С, D, ... и пишем их в столбец одна под другой.
3. Против каждой из местностей пишем во втором столбце число всех ведущих на нее мостов.
4. Четные местности отмечаем звездочкой при соответствующих буквах 1-го столбца.
5. В третьем столбце соответственно пишем половины четных чисел 2-го столбца, а если во втором столбце есть числа нечетные, то прибавляем к ним единицу и пишем в 3-м столбце половину полученного числа. (Каждое число 3-го столбца показывает число повторений соответствующей буквы.)
6. Находим сумму 3-го столбца.

Если эта последняя сумма 1) равна числу мостов или 2) больше его всего на одну единицу, то вопрос о полном обходе всех мостов по одному разу может быть решен. Но при этом надо иметь в виду, что в первом случае обход надо начинать с четной местности, а во втором - с нечетной. Для случая рассмотренной нами задачи о семи мостах будем иметь, значит, такую схему решения:

Так как 9 больше, чем 7 + 1, то, следовательно, задача неразрешима.