129. Интересная игра

Попробуйте со своим товарищем сыграть в следующую игру. Расположите на столе три кучки спичек. Например, в 12, 10 и 7 спичек. Игра заключается в том, чтобы поочередно брать из кучек некоторое, какое вам захочется, количество спичек, но каждый раз только из одной кучки. Можно взять и сразу целую кучку. Выигрывает тот, кто последним возьмет спички. Давайте для примера разыграем партию. Од* ного игрока обозначим А, другого Б.

Последним ходом игрок А выигрывает. Вопрос состоит в следующем: может ли А играть так, чтобы всегда выигрывать?

Решение. Ответ на вопрос неожиданно оказывается связанным с двоичной системой изображения чисел. Представим каждое из чисел 12, 10, 7 в двоичной системе:

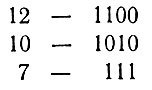
В каждом столбце получившейся таблицы, за исключением крайнего правого, стоит по две единицы. Первым ходом игрок А делает так, чтобы в каждом столбце стояло по две единицы или ни одной:

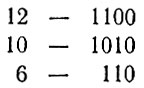
Своим ходом игрок Б нарушает это свойство, а игрок А его опять восстанавливает:

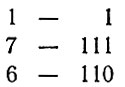
Если мы проследим за игрой далее, то увидим, что каждым ответным ходом игрок А восстанавливает нарушенное предыдущим ходом Б свойство таблицы содержать в каждом столбце четное количество единиц.

Назовем систему из трех целых неотрицательных чисел правильной, если после представления каждого числа в двоичной системе любой столбец содержит четное количество единиц, и неправильной в противном случае.

Легко видеть, что правильная система после любого хода становится неправильной, а из любой неправильной системы одним ходом всегда можно сделать правильную. Для этого давайте выберем самый левый столбец, где стоит нечетное число единиц, и то из чисел, которое в этом столбце имеет единицу, заменим на меньшее так, чтобы получилась правильная система. Это, очевидно, всегда можно сделать.

Если исходная система чисел неправильная (как в нашем примере), то начинающий игру всегда будет в выигрыше. Для этого он должен каждым своим ходом делать правильный набор чисел. Если же исходная система правильная (например, 12, 10, 6 или 13, 11, 6), то ваш противник, если он знает секрет игры, выиграет у вас, как бы вы ни играли. В этом случае делайте произвольные ходы в надежде, что противник ошибется и после его хода система чисел станет неправильной. Тогда перехватывайте инициативу и доводите игру до победного конца.

Можно раскладывать спички на 4, 5 и более кучек.

Вы выиграете, если будете играть так, чтобы после каждого вашего хода в любом столбце таблицы стояло четное число единиц.